| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
ddduuu
Forumaš(ica)

Pridružen/a: 16. 11. 2008. (12:31:48)
Postovi: (109)16
|
|
| [Vrh] |
|
JANKRI
Forumaš(ica)

Pridružen/a: 10. 07. 2008. (02:30:58)
Postovi: (10F)16
Spol: 
Lokacija: Zagreb
|
|
| [Vrh] |
|
ddduuu
Forumaš(ica)

Pridružen/a: 16. 11. 2008. (12:31:48)
Postovi: (109)16
|
|
| [Vrh] |
|
JANKRI
Forumaš(ica)

Pridružen/a: 10. 07. 2008. (02:30:58)
Postovi: (10F)16
Spol: 
Lokacija: Zagreb
|
 Postano: 23:21 ned, 16. 11. 2008 Naslov: Postano: 23:21 ned, 16. 11. 2008 Naslov: |
    |
|
|
[quote="ddduuu"]sve ovo skupa me zbunilo.. a npr da je f sa kojeg intervala u R bi bila injekcija.??. jer npr da je f funkcija ln, tada bi sa intervala <0,+besk> dala R,a ona je strogo rastuca pa je i injekcija. znaci u tom slucaju bi imali injektivnost..ili ne.. ufff sta san zbunjena..[/quote]
Aha, vidim što te buni, nama funkcija [latex]f[/latex] prema uvjetima zadatka mora biti definirana na cijelom skupu realnih brojeva.
| ddduuu (napisa): | | sve ovo skupa me zbunilo.. a npr da je f sa kojeg intervala u R bi bila injekcija.??. jer npr da je f funkcija ln, tada bi sa intervala <0,+besk> dala R,a ona je strogo rastuca pa je i injekcija. znaci u tom slucaju bi imali injektivnost..ili ne.. ufff sta san zbunjena.. |
Aha, vidim što te buni, nama funkcija  prema uvjetima zadatka mora biti definirana na cijelom skupu realnih brojeva. prema uvjetima zadatka mora biti definirana na cijelom skupu realnih brojeva.
|
|
| [Vrh] |
|
ddduuu
Forumaš(ica)

Pridružen/a: 16. 11. 2008. (12:31:48)
Postovi: (109)16
|
|
| [Vrh] |
|
Anna Lee
Forumaš(ica)


Pridružen/a: 11. 07. 2008. (00:49:44)
Postovi: (114)16
Spol: 
Lokacija: Zagreb
|
|
| [Vrh] |
|
JANKRI
Forumaš(ica)

Pridružen/a: 10. 07. 2008. (02:30:58)
Postovi: (10F)16
Spol: 
Lokacija: Zagreb
|
 Postano: 23:56 ned, 16. 11. 2008 Naslov: Postano: 23:56 ned, 16. 11. 2008 Naslov: |
    |
|
|
[quote="ddduuu"]ako imate vrimena i volje mozete i 5A rjesit:)[/quote]
Joj taj 5A, on je malo zeznut, no, tu je odgovor da takva funkcija postoji, jedan od primjera je [latex]f\left(x\right) = -2^x - 1[/latex], kako doći do toga? Krenemo od pretpostavke da takva funkcija postoji, te nakon provjeravanja svih uvjeta nađemo što sve za nju tada mora vrijediti... :-)
Dakle, "uzmemo" realne brojeve [latex]x_1[/latex] i [latex]x_2[/latex], neka je [latex]x_1 < x_2[/latex], tada mora biti [latex]f\left(x_1\right) > f\left(x_2\right)[/latex] i [latex]g\left(x_1\right) < g\left(x_2\right)[/latex].
Odnosno, [latex]4^{f\left(x_1\right)} - 2^{f\left(x_1\right)} < 4^{f\left(x_2\right)} - 2^{f\left(x_2\right)}[/latex]. Sada odmah vidimo da [latex]f[/latex] mora poprimati samo negativne vrijednosti, inače nejednakost očito ne vrijedi za sve [latex]x_1[/latex] i [latex]x_2[/latex], [latex]x_1<x_2[/latex]. Primjer takve padajuće funkcije koja poprima samo negativne vrijednosti je npr. [latex]f\left(x\right)=-2^x[/latex], no kad uvrstiimo to i malo sredimo izraz dobijemo da nam "smetaju" brojevi u intervalu [latex]\left\langle-1,\, 0\right\rangle[/latex], a njih se rješimo stavljajući [latex]f\left(x\right)=-2^x-1[/latex].
[size=9][color=#999999]Added after 10 minutes:[/color][/size]
[quote="Anna Lee"]5A je kolega jogrgur rjesio na prethodnoj stranici.[/quote]
Ispričavam se ako rješenje već negdje piše, ja to nisam primjetio :-)
| ddduuu (napisa): | | ako imate vrimena i volje mozete i 5A rjesit:) |
Joj taj 5A, on je malo zeznut, no, tu je odgovor da takva funkcija postoji, jedan od primjera je 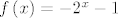 , kako doći do toga? Krenemo od pretpostavke da takva funkcija postoji, te nakon provjeravanja svih uvjeta nađemo što sve za nju tada mora vrijediti... , kako doći do toga? Krenemo od pretpostavke da takva funkcija postoji, te nakon provjeravanja svih uvjeta nađemo što sve za nju tada mora vrijediti... 
Dakle, "uzmemo" realne brojeve 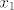 i i 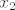 , neka je , neka je 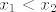 , tada mora biti , tada mora biti 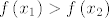 i i 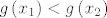 . .
Odnosno, 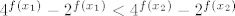 . Sada odmah vidimo da . Sada odmah vidimo da  mora poprimati samo negativne vrijednosti, inače nejednakost očito ne vrijedi za sve mora poprimati samo negativne vrijednosti, inače nejednakost očito ne vrijedi za sve 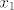 i i 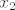 , , 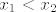 . Primjer takve padajuće funkcije koja poprima samo negativne vrijednosti je npr. . Primjer takve padajuće funkcije koja poprima samo negativne vrijednosti je npr. 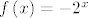 , no kad uvrstiimo to i malo sredimo izraz dobijemo da nam "smetaju" brojevi u intervalu , no kad uvrstiimo to i malo sredimo izraz dobijemo da nam "smetaju" brojevi u intervalu 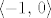 , a njih se rješimo stavljajući , a njih se rješimo stavljajući 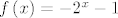 . .
Added after 10 minutes:
| Anna Lee (napisa): | | 5A je kolega jogrgur rjesio na prethodnoj stranici. |
Ispričavam se ako rješenje već negdje piše, ja to nisam primjetio 
|
|
| [Vrh] |
|
Gino
Forumaš(ica)

Pridružen/a: 11. 09. 2008. (10:54:06)
Postovi: (370)16
Lokacija: Pula
|
 Postano: 0:23 uto, 18. 11. 2008 Naslov: Postano: 0:23 uto, 18. 11. 2008 Naslov: |
    |
|
|
evo mojih rjesenja s kolokvija bio sam ona grupa koja je u 4. imala arctg...
pa ako se nade netko tko je bio ta grupa... ili ako znate nekog jer nisam nasao nikog pa nisam mogao usporedit...
[latex]1. \left\langle -\frac{1}{5},\, 0 \right] \cup \left[ 2, 1 + \sqrt{3} \right][/latex]
[latex]2. \mathsc{R}_f = \left\langle -1,\, \frac{1}{2} \right\rangle
[/latex]
[latex]f\left( \left\langle -\infty,\, 0 \right] \right) = \left[ 0,\, \frac{1}{2} \right\rangle[/latex]
[latex]3. f^{-1} \left( \left[ \right 1,\, 3 \rangle \right) = \bigcup\limits_{k \in \mathbb{Z}} { \left[- \frac{\pi}{2} + 2k\pi,\, \frac{\pi}{2} + 2k\pi \right] }[/latex]
[latex]4. \left( f \mid _{ \left\langle -\infty,\, 1 \right] } \right) ^{-1} \left(x\right) = \log_3{ \left( \frac{7 - \sqrt{49+4x}}{2} \right) }[/latex]
evo mojih rjesenja s kolokvija bio sam ona grupa koja je u 4. imala arctg...
pa ako se nade netko tko je bio ta grupa... ili ako znate nekog jer nisam nasao nikog pa nisam mogao usporedit...

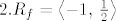
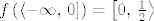
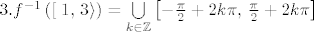
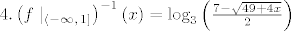
|
|
| [Vrh] |
|
bad_angel
Forumaš(ica)


Pridružen/a: 01. 11. 2008. (18:30:25)
Postovi: (43)16
Lokacija: svugdje po malo
|
 Postano: 9:59 uto, 18. 11. 2008 Naslov: Postano: 9:59 uto, 18. 11. 2008 Naslov: |
    |
|
|
Ja sam isto bila ta grupa!
1.,3. i 4. su mi isto tako ispali,a za 2.se ne sjecam.. kako je isao zadatak?
i je li krivo ako u 3.nisam napisala uniju ispred zagrade, i u cetvrtom sam zaboravila pisati restrikcije? ce mi to oduzeti bodove?
i zna li itko rjesenje 4. pod b? ja sam napisala da je injekcija, zbog kompozicije. tj.da su obje funkcije injekcije, jer je i arctg injekcija..
a,sjetila sam se drugog zadatka,tj.slike i tako mi je ispalo kao i tebi! :)
Ja sam isto bila ta grupa!
1.,3. i 4. su mi isto tako ispali,a za 2.se ne sjecam.. kako je isao zadatak?
i je li krivo ako u 3.nisam napisala uniju ispred zagrade, i u cetvrtom sam zaboravila pisati restrikcije? ce mi to oduzeti bodove?
i zna li itko rjesenje 4. pod b? ja sam napisala da je injekcija, zbog kompozicije. tj.da su obje funkcije injekcije, jer je i arctg injekcija..
a,sjetila sam se drugog zadatka,tj.slike i tako mi je ispalo kao i tebi! 
_________________
u raju je lijepo,ali u paklu je ekipa
|
|
| [Vrh] |
|
Gino
Forumaš(ica)

Pridružen/a: 11. 09. 2008. (10:54:06)
Postovi: (370)16
Lokacija: Pula
|
|
| [Vrh] |
|
|








