| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
ToMeK
Forumaš(ica)

Pridružen/a: 12. 09. 2008. (17:22:06)
Postovi: (BA)16
Spol: 
|
|
| [Vrh] |
|
Gino
Forumaš(ica)

Pridružen/a: 11. 09. 2008. (10:54:06)
Postovi: (370)16
Lokacija: Pula
|
|
| [Vrh] |
|
ToMeK
Forumaš(ica)

Pridružen/a: 12. 09. 2008. (17:22:06)
Postovi: (BA)16
Spol: 
|
|
| [Vrh] |
|
bad_angel
Forumaš(ica)


Pridružen/a: 01. 11. 2008. (18:30:25)
Postovi: (43)16
Lokacija: svugdje po malo
|
 Postano: 13:04 pet, 17. 4. 2009 Naslov: Postano: 13:04 pet, 17. 4. 2009 Naslov: |
    |
|
|
[quote="ToMeK"]kako bi derivirali Neka je f(x)= x/ 3.korjen od(1+x), Odredite f(n)(x).
[/quote]
to napišeš kao x puta (1+x)^(-1/3).
sada tražiš n-tu derivaciju produkta,gdje je 1 od članova polinom prvog stupnja, pa po Leibnizovoj formuli "preživljava",tj.nije jednako nuli, samo za k=0 i 1.
sad je samo pitanje koja je n-ta i (n-1) derivacija od (1+x)^(-1/3).
tu napišeš prvih par derivacija i uočiš neke stvari i ispadne da je n-ta derivacija
((-1)^n) što množi ((produkt kada k ide od 1 do n od (3k-2))/3^n) što množi (1+x)^(-(3n+1)/3)
ni ja neznam drugačije napisat,pa se nadam da si skužio. :? i nije skroz potpuno rješenje.
i sad za n-1 derivaciju samo umjesto n uvrstiš n-1. i nemoj zaboravit n povrh 1 ispred n-1 derivacije :wink:
i nadam se da ti je jasno zašto je ovakva n-ta derivacija,da ne pišem sve, ali ako nije,reci..
| ToMeK (napisa): | kako bi derivirali Neka je f(x)= x/ 3.korjen od(1+x), Odredite f(n)(x).
|
to napišeš kao x puta (1+x)^(-1/3).
sada tražiš n-tu derivaciju produkta,gdje je 1 od članova polinom prvog stupnja, pa po Leibnizovoj formuli "preživljava",tj.nije jednako nuli, samo za k=0 i 1.
sad je samo pitanje koja je n-ta i (n-1) derivacija od (1+x)^(-1/3).
tu napišeš prvih par derivacija i uočiš neke stvari i ispadne da je n-ta derivacija
((-1)^n) što množi ((produkt kada k ide od 1 do n od (3k-2))/3^n) što množi (1+x)^(-(3n+1)/3)
ni ja neznam drugačije napisat,pa se nadam da si skužio.  i nije skroz potpuno rješenje. i nije skroz potpuno rješenje.
i sad za n-1 derivaciju samo umjesto n uvrstiš n-1. i nemoj zaboravit n povrh 1 ispred n-1 derivacije 
i nadam se da ti je jasno zašto je ovakva n-ta derivacija,da ne pišem sve, ali ako nije,reci..
_________________
u raju je lijepo,ali u paklu je ekipa
|
|
| [Vrh] |
|
tidus
Forumaš(ica)


Pridružen/a: 16. 02. 2009. (12:47:59)
Postovi: (A5)16
Spol: 
|
|
| [Vrh] |
|
Gino
Forumaš(ica)

Pridružen/a: 11. 09. 2008. (10:54:06)
Postovi: (370)16
Lokacija: Pula
|
 Postano: 14:09 pon, 20. 4. 2009 Naslov: Postano: 14:09 pon, 20. 4. 2009 Naslov: |
    |
|
|
tebi nije jasan Arshx, ne nisam dobro napisao...
nije ti jasan Arshx, mislim nije ti jasno kako doc do n-te derivacije :D :D :D :D
nema veze koja je funkcija u pitanju, ako si dosao do tog dijela... probaj sad pogledat kako sam ja nasao n-tu derivaciju za sin ili cos na 2 od x, isto sam dobio neku rekurzivnu relaciju, i onda derivirao sve n-2 puta, i 'razvio' po laibnicu... to je cijela mudrost, nemoj da te zbuni sta sam ja zapravo dosao da formule za n-1. derivaciju a kasnije napisao za n-tu, to samo svakom clanu koji ima veze sa n dodas 1, mislim to nije dobro receno i to al valjda je jasno sta mislim
[size=9][color=#999999]Added after 2 minutes:[/color][/size]
zapravo to si skuzio... glup sam
ono sta slijedi je cisto rapisivanje koje me uvijek zbuni
uvrstis konkretni n i gledas kako se stvar odvija pa skuzis koja je opca formula
tebi nije jasan Arshx, ne nisam dobro napisao...
nije ti jasan Arshx, mislim nije ti jasno kako doc do n-te derivacije    
nema veze koja je funkcija u pitanju, ako si dosao do tog dijela... probaj sad pogledat kako sam ja nasao n-tu derivaciju za sin ili cos na 2 od x, isto sam dobio neku rekurzivnu relaciju, i onda derivirao sve n-2 puta, i 'razvio' po laibnicu... to je cijela mudrost, nemoj da te zbuni sta sam ja zapravo dosao da formule za n-1. derivaciju a kasnije napisao za n-tu, to samo svakom clanu koji ima veze sa n dodas 1, mislim to nije dobro receno i to al valjda je jasno sta mislim
Added after 2 minutes:
zapravo to si skuzio... glup sam
ono sta slijedi je cisto rapisivanje koje me uvijek zbuni
uvrstis konkretni n i gledas kako se stvar odvija pa skuzis koja je opca formula
_________________
Mario Berljafa
|
|
| [Vrh] |
|
ma
Forumaš(ica)


Pridružen/a: 27. 01. 2007. (12:06:50)
Postovi: (347)16
Spol: 
|
 Postano: 14:20 pon, 20. 4. 2009 Naslov: Postano: 14:20 pon, 20. 4. 2009 Naslov: |
    |
|
|
[quote="tidus"]meni još uvijek nije jasan Arshx.
dobijem:
y(0)^(n-1 -derivaciju)=-(n-2)*(y(0)^3)^(n-3 -derivaciju)
što da sada radim Question Confused[/quote]
ovo bi trebalo biti ok uz iznimku da ti fali kvadrat kod n-2 ([latex](n-2)^2[/latex]).
sad to treba dovesti do 'nižih' derivacija.
znači, ako je [latex]y^{(n-1)}(0)=-(n-2)^2 [y^{(n-3)}(0)]^3[/latex], onda ti je i [latex]y^{(n-3)}(0)=-(n-2)^2 [y^{(n-5)}(0)]^3[/latex], itd.
onda skužiš da ćeš za parne n dobiti 0, jer je nakon nekog koraka n-2=0, a neparni će ići sve do prve derivacije u nuli, a to je 1. sad još malo razmisliš kako sve to skupiti u jedan zapis (koliko će minusa biti i koliki će biti konačni umnožak ovisno o n)
| tidus (napisa): | meni još uvijek nije jasan Arshx.
dobijem:
y(0)^(n-1 -derivaciju)=-(n-2)*(y(0)^3)^(n-3 -derivaciju)
što da sada radim Question Confused |
ovo bi trebalo biti ok uz iznimku da ti fali kvadrat kod n-2 (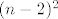 ). ).
sad to treba dovesti do 'nižih' derivacija.
znači, ako je 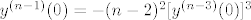 , onda ti je i , onda ti je i 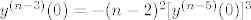 , itd. , itd.
onda skužiš da ćeš za parne n dobiti 0, jer je nakon nekog koraka n-2=0, a neparni će ići sve do prve derivacije u nuli, a to je 1. sad još malo razmisliš kako sve to skupiti u jedan zapis (koliko će minusa biti i koliki će biti konačni umnožak ovisno o n)
_________________
ima let u finish
Zadnja promjena: ma; 21:12 pon, 20. 4. 2009; ukupno mijenjano 2 put/a.
|
|
| [Vrh] |
|
tidus
Forumaš(ica)


Pridružen/a: 16. 02. 2009. (12:47:59)
Postovi: (A5)16
Spol: 
|
|
| [Vrh] |
|
ma
Forumaš(ica)


Pridružen/a: 27. 01. 2007. (12:06:50)
Postovi: (347)16
Spol: 
|
 Postano: 21:14 pon, 20. 4. 2009 Naslov: Postano: 21:14 pon, 20. 4. 2009 Naslov: |
    |
|
|
[quote="tidus"]zahvaljujem. ali još ostaje problem gomilanja potencija. jer svako novo uvrštavanje rekurzije diže račun na treću, pa je onda potencija od (n-2) ogromna. može li se to onda ostaviti tako na kolokviju?[/quote]
pa u principu ne, od tebe se očekuje da pojednostaviš što je više moguće.
sad vidim da sam krivo napisao u prethodnom postu (dolje ispravak).
btw, pogledaj si posljednji post na prethodnoj strani- tamo je rješenje.
[size=9][color=#999999]Added after 6 minutes:[/color][/size]
[i]ispravak[/i]
znači, ako je [latex]y^{(n-1)}(0)=-(n-2)^2 [y^{(n-3)}(0)]^3[/latex], onda ti je [latex]y^{(n-3)}(0)=-(n-4)^2 [y^{(n-5)}(0)]^3[/latex], itd.
znači ne gomilaju se potencije od n-2, nego dobivaš dvofaktorijele. sorry.
nadam se da je jasnije 8)
| tidus (napisa): | | zahvaljujem. ali još ostaje problem gomilanja potencija. jer svako novo uvrštavanje rekurzije diže račun na treću, pa je onda potencija od (n-2) ogromna. može li se to onda ostaviti tako na kolokviju? |
pa u principu ne, od tebe se očekuje da pojednostaviš što je više moguće.
sad vidim da sam krivo napisao u prethodnom postu (dolje ispravak).
btw, pogledaj si posljednji post na prethodnoj strani- tamo je rješenje.
Added after 6 minutes:
ispravak
znači, ako je 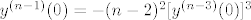 , onda ti je , onda ti je 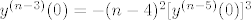 , itd. , itd.
znači ne gomilaju se potencije od n-2, nego dobivaš dvofaktorijele. sorry.
nadam se da je jasnije 
_________________
ima let u finish
|
|
| [Vrh] |
|
|










