| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
Tindariel
Forumaš(ica)

Pridružen/a: 03. 12. 2008. (00:49:03)
Postovi: (71)16
Spol: 
Lokacija: Zagreb
|
|
| [Vrh] |
|
kenny
Petica iz zalaganja


Pridružen/a: 28. 03. 2003. (09:18:36)
Postovi: (3B7)16
Spol: 
Lokacija: ...somewhere over the rainbow...
|
|
| [Vrh] |
|
Tindariel
Forumaš(ica)

Pridružen/a: 03. 12. 2008. (00:49:03)
Postovi: (71)16
Spol: 
Lokacija: Zagreb
|
|
| [Vrh] |
|
Spectre
Forumaš(ica)


Pridružen/a: 02. 10. 2006. (16:58:05)
Postovi: (167)16
Spol: 
|
 Postano: 0:46 uto, 21. 4. 2009 Naslov: Postano: 0:46 uto, 21. 4. 2009 Naslov: |
    |
|
|
Po meni, [latex]\lim_{x \to 0^{-}}\frac{1}{x^2} \rightarrow +\infty[/latex].
Svi x-ići lijevo od nule su negativni, te će kvadriranjem postati pozitivni. Tako da je to isto kao da piše [latex]\lim_{x \to 0^{+}}\frac{1}{x^{2}} \rightarrow +\infty[/latex], odnosno [latex]\lim_{x \to 0^{+}}\frac{1}{x} \rightarrow +\infty[/latex].
No, ja bih originalni limes riješio ovako (preko L'Hospitala):
[latex]
\lim_{x \to 0^{-}}\frac{\ x+e^{ \frac{1}{x}}}{x} =
\lim_{x \to 0^{-}}\frac{1-e^\frac{1}{x} \cdot \frac{1}{x^{2}}}{1} =
1 - \lim_{x \to 0^{-}}e^\frac{1}{x} \cdot \frac{1}{x^{2}} =
1 - \lim_{x \to 0^{-}}\frac{e^\frac{1}{x}}{x^{2}} =
1 - \frac{e^{-\infty}}{-0^{2}} =
1 - \frac{0}{0}[/latex]
Uff... Nisam ništa postigao. Predajem se za večeras :)
Po meni, 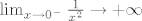 . .
Svi x-ići lijevo od nule su negativni, te će kvadriranjem postati pozitivni. Tako da je to isto kao da piše 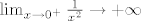 , odnosno , odnosno 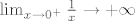 . .
No, ja bih originalni limes riješio ovako (preko L'Hospitala):
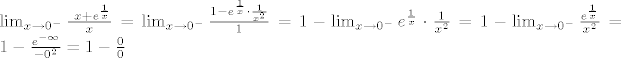
Uff... Nisam ništa postigao. Predajem se za večeras 
_________________
Cry havoc, and let loose the dogs of war!
Zadnja promjena: Spectre; 1:15 uto, 21. 4. 2009; ukupno mijenjano 5 put/a.
|
|
| [Vrh] |
|
rafaelm
Forumaš(ica)


Pridružen/a: 24. 12. 2006. (13:30:11)
Postovi: (21F)16
Spol: 
Lokacija: Zagreb
|
|
| [Vrh] |
|
Tindariel
Forumaš(ica)

Pridružen/a: 03. 12. 2008. (00:49:03)
Postovi: (71)16
Spol: 
Lokacija: Zagreb
|
 Postano: 1:10 uto, 21. 4. 2009 Naslov: Postano: 1:10 uto, 21. 4. 2009 Naslov: |
    |
|
|
Joj, stvarno. :oops: Ide u +beskonačno. Kad ne razmišljam... al dobro, to mi ništa ne mijenja situaciju. :(
[size=9][color=#999999]Added after 5 minutes:[/color][/size]
[quote]No, ja bih originalni limes riješio ovako (preko L'Hospitala):
[latex]
\lim_{x \to 0^{-}}\frac{\ x+e^{ \frac{1}{x}}}{x} =
\lim_{x \to 0^{-}}\frac{1-e^\frac{1}{x} \cdot \frac{1}{x^{2}}}{1} =
1 - \lim_{x \to 0^{-}}e^\frac{1}{x} \cdot \frac{1}{x^{2}} =
1 - \lim_{x \to 0^{-}}\frac{e^\frac{1}{x}}{x^{2}} =
1 - \lim_{x \to 0^{-}}\frac{e^{-\infty}}{-0^{2}} =
\lim_{x \to 0^{-}}\frac{0}{0} =
1 - 0 =
1[/latex][/quote]
Smijemo za 0/0 reći da je 0? :o Jer ako je tako, onda nema smisla uopće išta raditi, jer odmah stoji da 1 + 0/0 (ako se uvrsti nula umjesto x)
Joj, stvarno.  Ide u +beskonačno. Kad ne razmišljam... al dobro, to mi ništa ne mijenja situaciju. Ide u +beskonačno. Kad ne razmišljam... al dobro, to mi ništa ne mijenja situaciju. 
Added after 5 minutes:
| Citat: | No, ja bih originalni limes riješio ovako (preko L'Hospitala):
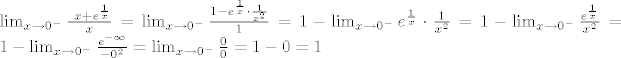 |
Smijemo za 0/0 reći da je 0?  Jer ako je tako, onda nema smisla uopće išta raditi, jer odmah stoji da 1 + 0/0 (ako se uvrsti nula umjesto x) Jer ako je tako, onda nema smisla uopće išta raditi, jer odmah stoji da 1 + 0/0 (ako se uvrsti nula umjesto x)
|
|
| [Vrh] |
|
Spectre
Forumaš(ica)


Pridružen/a: 02. 10. 2006. (16:58:05)
Postovi: (167)16
Spol: 
|
|
| [Vrh] |
|
Tindariel
Forumaš(ica)

Pridružen/a: 03. 12. 2008. (00:49:03)
Postovi: (71)16
Spol: 
Lokacija: Zagreb
|
|
| [Vrh] |
|
vsego
Site Admin


Pridružen/a: 06. 10. 2002. (22:07:09)
Postovi: (3562)16
Spol: 
Lokacija: /sbin/init
|
|
| [Vrh] |
|
Tindariel
Forumaš(ica)

Pridružen/a: 03. 12. 2008. (00:49:03)
Postovi: (71)16
Spol: 
Lokacija: Zagreb
|
|
| [Vrh] |
|
ma
Forumaš(ica)


Pridružen/a: 27. 01. 2007. (12:06:50)
Postovi: (347)16
Spol: 
|
|
| [Vrh] |
|
Tindariel
Forumaš(ica)

Pridružen/a: 03. 12. 2008. (00:49:03)
Postovi: (71)16
Spol: 
Lokacija: Zagreb
|
|
| [Vrh] |
|
Spectre
Forumaš(ica)


Pridružen/a: 02. 10. 2006. (16:58:05)
Postovi: (167)16
Spol: 
|
|
| [Vrh] |
|
|

















