| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
l00d
Forumaš(ica)
Pridružen/a: 03. 05. 2009. (13:02:25)
Postovi: (2)16
|
 Postano: 13:21 ned, 3. 5. 2009 Naslov: Derivacija složene funkcije! |
    |
|
|
Pozdrav. Pošto sam prvi put na ovome forumu, možda nisam u dobar podforum ubacio zadatak, ako je tako, nadam se da će se mod pobrinuti.
U projektu iz matematike dobio sam jedan zadatak (a taj zadatak spada pod nastavnu cjelinu Derivacija složene funkcije, ako ima ikakve veze.). A zadatak glasi:
- Polumjer kruga povećava se brzinom 2 cm/s. Kolikom se brzinom povećava njegova površina, u trenutku kad je polumjer jednak 12 cm?
Najljepša hvala!
[color=blue]Mod edit: "Čistilište" je pravi podforum za takva pitanja (prebačeno).[/color]
Pozdrav. Pošto sam prvi put na ovome forumu, možda nisam u dobar podforum ubacio zadatak, ako je tako, nadam se da će se mod pobrinuti.
U projektu iz matematike dobio sam jedan zadatak (a taj zadatak spada pod nastavnu cjelinu Derivacija složene funkcije, ako ima ikakve veze.). A zadatak glasi:
- Polumjer kruga povećava se brzinom 2 cm/s. Kolikom se brzinom povećava njegova površina, u trenutku kad je polumjer jednak 12 cm?
Najljepša hvala!
Mod edit: "Čistilište" je pravi podforum za takva pitanja (prebačeno).
|
|
| [Vrh] |
|
StateOfConsciousness
Forumaš s poteškoćama u pisanju
Pridružen/a: 22. 07. 2008. (16:08:24)
Postovi: (8A)16
|
| Postano: 18:09 uto, 5. 5. 2009 Naslov: Re: Derivacija složene funkcije! |
|
|
|
[quote="l00d"]Pozdrav. Pošto sam prvi put na ovome forumu, možda nisam u dobar podforum ubacio zadatak, ako je tako, nadam se da će se mod pobrinuti.
U projektu iz matematike dobio sam jedan zadatak (a taj zadatak spada pod nastavnu cjelinu Derivacija složene funkcije, ako ima ikakve veze.). A zadatak glasi:
- Polumjer kruga povećava se brzinom 2 cm/s. Kolikom se brzinom povećava njegova površina, u trenutku kad je polumjer jednak 12 cm?
Najljepša hvala!
[color=blue]Mod edit: "Čistilište" je pravi podforum za takva pitanja (prebačeno).[/color][/quote]
Mislim da ti to ovako ide:
Znači, vrijedi dr/dt = 2cm/s, a traži se dP/dt kada je r=12cm.
Jer je dP/dt=dP/dr x dr/dt (x prestavlja množenje) a P(r)=r^2 x pi, to je dP/dt=2r x pi x 2cm/s, a za r=12cm to je jednako 48pi cm^2 /s
| l00d (napisa): | Pozdrav. Pošto sam prvi put na ovome forumu, možda nisam u dobar podforum ubacio zadatak, ako je tako, nadam se da će se mod pobrinuti.
U projektu iz matematike dobio sam jedan zadatak (a taj zadatak spada pod nastavnu cjelinu Derivacija složene funkcije, ako ima ikakve veze.). A zadatak glasi:
- Polumjer kruga povećava se brzinom 2 cm/s. Kolikom se brzinom povećava njegova površina, u trenutku kad je polumjer jednak 12 cm?
Najljepša hvala!
Mod edit: "Čistilište" je pravi podforum za takva pitanja (prebačeno). |
Mislim da ti to ovako ide:
Znači, vrijedi dr/dt = 2cm/s, a traži se dP/dt kada je r=12cm.
Jer je dP/dt=dP/dr x dr/dt (x prestavlja množenje) a P(r)=r^2 x pi, to je dP/dt=2r x pi x 2cm/s, a za r=12cm to je jednako 48pi cm^2 /s
_________________
Look at every path closely and deliberately. Try it as many times as you think necessary. Then ask yourself,
and yourself alone, one question . . . Does this path have a heart? If it does, the path is good; if it doesn’t it is of no use.
Carlos Castaneda, The Teachings of Don juan
|
|
| [Vrh] |
|
Gost
|
| Postano: 19:38 uto, 5. 5. 2009 Naslov: |
|
|
|
Je, rješenje je takvo, dobro misliš :)
Ali nisam baš shvatio postupak, pa ako mi možeš laički riječima ukratko, tj. zanima me šta je "dr/dt", "dP/dt", zašto je "dP/dt=dP/dr x dr/dt" i odakle " dP/dt=2r x pi x 2cm/s". Bio bih jako zahvalan!
Je, rješenje je takvo, dobro misliš 
Ali nisam baš shvatio postupak, pa ako mi možeš laički riječima ukratko, tj. zanima me šta je "dr/dt", "dP/dt", zašto je "dP/dt=dP/dr x dr/dt" i odakle " dP/dt=2r x pi x 2cm/s". Bio bih jako zahvalan!
|
|
| [Vrh] |
|
StateOfConsciousness
Forumaš s poteškoćama u pisanju
Pridružen/a: 22. 07. 2008. (16:08:24)
Postovi: (8A)16
|
| Postano: 19:50 uto, 5. 5. 2009 Naslov: |
|
|
|
[quote="Anonymous"]Je, rješenje je takvo, dobro misliš :)
Ali nisam baš shvatio postupak, pa ako mi možeš laički riječima ukratko, tj. zanima me šta je "dr/dt", "dP/dt", zašto je "dP/dt=dP/dr x dr/dt" i odakle " dP/dt=2r x pi x 2cm/s". Bio bih jako zahvalan![/quote]
dr/dt ti je brzina rasta polumjera (derivacija polumjera po vremenu), r je funkcija vremena
dP/dt ti je brzina rasta površine (derivacija površine po vremenu), P je isto funkcija vremena
dP/dt= dP/dr x dr/dt ti je pravilo za deriviranje složenih funkcija, prvo P predstavlja složenu funkciju P(r(t)), površinu kao funkciju radijusa koji je funkcija vremena,tj. P kao složenu funkciju vremena a drugo P predstavlja površinu kao funkciju od r, P(r), sada kao nesloženu funkciju a dP/dt=2r x pi x 2cm/s dobiješ kada uvrstiš dr/dt=2cm/s a 2r x pi dobiješ kada deriviraš dP/dr jer je P(r)= r^2 x pi.
Eto.
| Anonymous (napisa): | Je, rješenje je takvo, dobro misliš
Ali nisam baš shvatio postupak, pa ako mi možeš laički riječima ukratko, tj. zanima me šta je "dr/dt", "dP/dt", zašto je "dP/dt=dP/dr x dr/dt" i odakle " dP/dt=2r x pi x 2cm/s". Bio bih jako zahvalan! |
dr/dt ti je brzina rasta polumjera (derivacija polumjera po vremenu), r je funkcija vremena
dP/dt ti je brzina rasta površine (derivacija površine po vremenu), P je isto funkcija vremena
dP/dt= dP/dr x dr/dt ti je pravilo za deriviranje složenih funkcija, prvo P predstavlja složenu funkciju P(r(t)), površinu kao funkciju radijusa koji je funkcija vremena,tj. P kao složenu funkciju vremena a drugo P predstavlja površinu kao funkciju od r, P(r), sada kao nesloženu funkciju a dP/dt=2r x pi x 2cm/s dobiješ kada uvrstiš dr/dt=2cm/s a 2r x pi dobiješ kada deriviraš dP/dr jer je P(r)= r^2 x pi.
Eto.
_________________
Look at every path closely and deliberately. Try it as many times as you think necessary. Then ask yourself,
and yourself alone, one question . . . Does this path have a heart? If it does, the path is good; if it doesn’t it is of no use.
Carlos Castaneda, The Teachings of Don juan
|
|
| [Vrh] |
|
kenny
Petica iz zalaganja
Pridružen/a: 28. 03. 2003. (09:18:36)
Postovi: (3B7)16
Spol: 
Lokacija: ...somewhere over the rainbow...
|
|
| [Vrh] |
|
l00d
Forumaš(ica)
Pridružen/a: 03. 05. 2009. (13:02:25)
Postovi: (2)16
|
|
| [Vrh] |
|
kenny
Petica iz zalaganja
Pridružen/a: 28. 03. 2003. (09:18:36)
Postovi: (3B7)16
Spol:
Lokacija: ...somewhere over the rainbow...
|
|
| [Vrh] |
|
vsego
Site Admin
Pridružen/a: 06. 10. 2002. (22:07:09)
Postovi: (3560)16
Spol: 
Lokacija: /sbin/init
|
| Postano: 22:15 uto, 5. 5. 2009 Naslov: |
|
|
|
@l00d: A je l' ti jasnije ako umjesto dr/dt pises r'(t), a umjesto dP/dt napises P'(t), pri cemu su je r(t) radijus u trenutku t, a P(t) povrsina u trenutku t? :D Pravilo deriviranja slozene funkcije
[latex]P(t) = r(t)^2 \pi[/latex]
je
[latex]P'(t) = 2 r(t) r'(t) \pi[/latex]
(prvo deriviras kvadratnu funkciju, a zatim njen argument r(t))
Ako ti je tako jasno, to je isto sto je i StateOfConsciousness napisao, samo sto "njegov" zapis naglasava varijablu po kojoj se derivira (sto ovdje ne treba jer su sve funkcije ovisne o istoj varijabli t i po njoj deriviramo). :)
Ako ti niti ovaj "moj" zapis nije poznat... :neznam: Tako se, IIRC, rade derivacije u srednjoj skoli i ja ne znam za jednostavniji oblik. :?
@l00d: A je l' ti jasnije ako umjesto dr/dt pises r'(t), a umjesto dP/dt napises P'(t), pri cemu su je r(t) radijus u trenutku t, a P(t) povrsina u trenutku t?  Pravilo deriviranja slozene funkcije
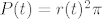
je
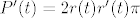
(prvo deriviras kvadratnu funkciju, a zatim njen argument r(t))
Ako ti je tako jasno, to je isto sto je i StateOfConsciousness napisao, samo sto "njegov" zapis naglasava varijablu po kojoj se derivira (sto ovdje ne treba jer su sve funkcije ovisne o istoj varijabli t i po njoj deriviramo).
Ako ti niti ovaj "moj" zapis nije poznat...  Tako se, IIRC, rade derivacije u srednjoj skoli i ja ne znam za jednostavniji oblik. 
_________________ U pravilu ignoriram pitanja u krivim topicima i kodove koji nisu u [code]...[/code] blokovima.
Takodjer, OBJASNITE sto vas muci! "Sto mi je krivo?", bez opisa u cemu je problem, rijetko ce zadobiti moju paznju.  |
|
| [Vrh] |
|
|
to NIJE nesto sto se na redovnoj nastavi radi.