| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
bad_angel
Forumaš(ica)


Pridružen/a: 01. 11. 2008. (18:30:25)
Postovi: (43)16
Lokacija: svugdje po malo
|
|
| [Vrh] |
|
Gino
Forumaš(ica)

Pridružen/a: 11. 09. 2008. (10:54:06)
Postovi: (370)16
Lokacija: Pula
|
|
| [Vrh] |
|
bad_angel
Forumaš(ica)


Pridružen/a: 01. 11. 2008. (18:30:25)
Postovi: (43)16
Lokacija: svugdje po malo
|
|
| [Vrh] |
|
bad_angel
Forumaš(ica)


Pridružen/a: 01. 11. 2008. (18:30:25)
Postovi: (43)16
Lokacija: svugdje po malo
|
|
| [Vrh] |
|
Gino
Forumaš(ica)

Pridružen/a: 11. 09. 2008. (10:54:06)
Postovi: (370)16
Lokacija: Pula
|
|
| [Vrh] |
|
tidus
Forumaš(ica)


Pridružen/a: 16. 02. 2009. (12:47:59)
Postovi: (A5)16
Spol: 
|
|
| [Vrh] |
|
Grga
Forumaš(ica)


Pridružen/a: 23. 12. 2004. (23:05:23)
Postovi: (280)16
Spol: 
|
|
| [Vrh] |
|
tidus
Forumaš(ica)


Pridružen/a: 16. 02. 2009. (12:47:59)
Postovi: (A5)16
Spol: 
|
|
| [Vrh] |
|
ivek imudaš
Forumaš(ica)


Pridružen/a: 13. 11. 2007. (18:41:02)
Postovi: (67)16
Spol: 
|
|
| [Vrh] |
|
Gino
Forumaš(ica)

Pridružen/a: 11. 09. 2008. (10:54:06)
Postovi: (370)16
Lokacija: Pula
|
|
| [Vrh] |
|
Grga
Forumaš(ica)


Pridružen/a: 23. 12. 2004. (23:05:23)
Postovi: (280)16
Spol: 
|
|
| [Vrh] |
|
tidus
Forumaš(ica)


Pridružen/a: 16. 02. 2009. (12:47:59)
Postovi: (A5)16
Spol: 
|
|
| [Vrh] |
|
Gino
Forumaš(ica)

Pridružen/a: 11. 09. 2008. (10:54:06)
Postovi: (370)16
Lokacija: Pula
|
|
| [Vrh] |
|
Grga
Forumaš(ica)


Pridružen/a: 23. 12. 2004. (23:05:23)
Postovi: (280)16
Spol: 
|
 Postano: 22:19 pet, 26. 6. 2009 Naslov: Postano: 22:19 pet, 26. 6. 2009 Naslov: |
    |
|
|
[quote="tidus"]HVALA :D
Nešto mi ipak nije jasno... :oops:
Zašto suma od 1/(n^2) teži u 1 i zažto suma od 1-1/((n+1)^2) također teži u jedan?[/quote]
Radi se o parcijalnim sumama, dakle [latex]S_n = \sum_1^n (\frac{1}{n^2} - \frac{1}{(n+1)^2})[/latex]
[latex]S_1 = 1 - \frac{1}{(1+1)^2}[/latex]
[latex]S_2 = 1 - \frac{1}{(1+1)^2} + \frac{1}{2^2} - \frac{1}{(2 + 1)^2} = 1 - \frac{1}{(2 + 1)^2}[/latex]
I tako dalje, raspises i vidis da se svaki put pokrate, tu metodu zovemo teleskopiranje, a zapravo se radi o matematickoj indukciji, jer pretpostavimo da vrijedi [latex]S_n = 1 - \frac{1}{(n+1)^2}[/latex]
Bazu imamo, pa gledamo [latex]S_{n + 1} = S_n + \frac{1}{(n + 1)^2} - \frac{1}{(n + 2)^2} = 1 - \frac{1}{(n+1)^2} + \frac{1}{(n + 1)^2} - \frac{1}{(n + 2)^2} = 1 - \frac{1}{((n + 1) + 1)^2}[/latex]
Suma reda je definirana upravo kao limes niza parcijalnih suma, dakle
[latex]\displaystyle\lim_{n \to \infty}{S_n} = \lim_{n \to \infty}{1 - \frac{1}{(n+1)^2}}= 1 - 0 = 1[/latex]
Suma reda (1/n)^2 je (pi^2)/6, ali mislim da izracunavanje te sume bas i ne spada u okvire kolegija, samo pokazivanje da je red konvergentan :)
| tidus (napisa): | HVALA 
Nešto mi ipak nije jasno... 
Zašto suma od 1/(n^2) teži u 1 i zažto suma od 1-1/((n+1)^2) također teži u jedan? |
Radi se o parcijalnim sumama, dakle 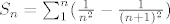
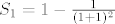
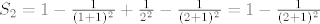
I tako dalje, raspises i vidis da se svaki put pokrate, tu metodu zovemo teleskopiranje, a zapravo se radi o matematickoj indukciji, jer pretpostavimo da vrijedi 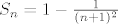
Bazu imamo, pa gledamo 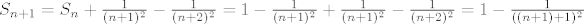
Suma reda je definirana upravo kao limes niza parcijalnih suma, dakle
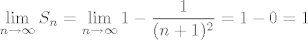
Suma reda (1/n)^2 je (pi^2)/6, ali mislim da izracunavanje te sume bas i ne spada u okvire kolegija, samo pokazivanje da je red konvergentan 
_________________
Bri
|
|
| [Vrh] |
|
tidus
Forumaš(ica)


Pridružen/a: 16. 02. 2009. (12:47:59)
Postovi: (A5)16
Spol: 
|
|
| [Vrh] |
|
Tindariel
Forumaš(ica)

Pridružen/a: 03. 12. 2008. (00:49:03)
Postovi: (71)16
Spol: 
Lokacija: Zagreb
|
|
| [Vrh] |
|
JANKRI
Forumaš(ica)

Pridružen/a: 10. 07. 2008. (02:30:58)
Postovi: (10F)16
Spol: 
Lokacija: Zagreb
|
 Postano: 13:53 ned, 28. 6. 2009 Naslov: Postano: 13:53 ned, 28. 6. 2009 Naslov: |
    |
|
|
[b]3.3.d[/b]
Prvo, nađimo adicijsku formulu za [latex]\arctan[/latex], neka su [latex]x,\, y \in \mathbb{R}[/latex], sada znamo da je
[latex]\tan{\left(\arctan{x}+\arctan{y}\right)}=\frac{x+y}{1-xy}[/latex], iz ovoga direktno dobivamo da je
[latex]\arctan{x}+\arctan{y}=\arctan{\frac{x+y}{1-xy}},\ \forall x,\, y \in \mathbb{R}[/latex].
Neka je [latex]S_n = \sum\limits_{k=1}^{n}{\arctan{\frac{1}{2k^2}}}[/latex], lako (koristeći dobivenu adicijsku formulu) nalazimo da je [latex]S_1=\arctan{\frac{1}{2}}[/latex], [latex]S_2=\arctan{\frac{2}{3}}[/latex], [latex]S_3=\arctan{\frac{3}{4}}[/latex]. U ovom trenutku naslućujemo da je
[latex]S_n = \arctan{\frac{n}{n+1}},\ \forall n \in \mathbb{N}[/latex].
Dokaz provodimo matematičkom indukcijom po [latex]n[/latex], baza indukcije [latex]\left(S_1=\arctan{\frac{1}{2}}\right)[/latex] je ispunjena, pretpostavimo da tvrdnja vrijedi za neki [latex]n \in \mathbb{N}[/latex], sada je
[latex]S_{n+1}=\arctan{\frac{n}{n+1}}+\arctan{\frac{1}{2\left(n+1\right)^2}}[/latex], korištenjem dobivene adicijske formule i sređivanjen, dobivamo
[latex]S_{n+1}=\arctan{\frac{2n^3+4n^2+3n+1}{2n^3+6n^2+5n+2}}[/latex].
Kako mi želimo da je [latex]S_{n+1}=\frac{n+1}{n+2}[/latex] dijelimo polinom u brojniku s [latex]n+1[/latex], a polinom u nazivniku s [latex]n+2[/latex] nadajući se da ćemo dobiti jednake kvocijente (u protivnom je naša slutnja kriva). Vrijedi
[latex]\left(2n^3+4n^2+3n+1\right) : \left(n+1\right) = 2n^2+2n+1[/latex],
[latex]\left(2n^3+6n^2+5n+2\right) : \left(n+2\right) = 2n^2+2n+1[/latex].
Ovime smo pokazali da je
[latex]S_n=\arctan{\frac{n}{n+1}},\ \forall n \in \mathbb{N}[/latex].
Konačno,
[latex]\sum\limits_{n=1}^{\infty}{\arctan{\frac{1}{2n^2}}}=\lim\limits_{n \to \infty}{S_n} = \arctan{1} = \frac{\pi}{4}[/latex].
3.3.d
Prvo, nađimo adicijsku formulu za 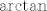 , neka su , neka su 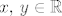 , sada znamo da je , sada znamo da je
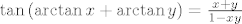 , iz ovoga direktno dobivamo da je , iz ovoga direktno dobivamo da je
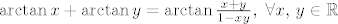 . .
Neka je 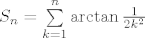 , lako (koristeći dobivenu adicijsku formulu) nalazimo da je , lako (koristeći dobivenu adicijsku formulu) nalazimo da je 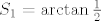 , , 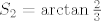 , , 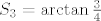 . U ovom trenutku naslućujemo da je . U ovom trenutku naslućujemo da je
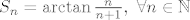 . .
Dokaz provodimo matematičkom indukcijom po  , baza indukcije , baza indukcije 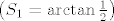 je ispunjena, pretpostavimo da tvrdnja vrijedi za neki je ispunjena, pretpostavimo da tvrdnja vrijedi za neki  , sada je , sada je
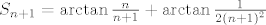 , korištenjem dobivene adicijske formule i sređivanjen, dobivamo , korištenjem dobivene adicijske formule i sređivanjen, dobivamo
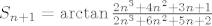 . .
Kako mi želimo da je 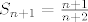 dijelimo polinom u brojniku s dijelimo polinom u brojniku s 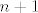 , a polinom u nazivniku s , a polinom u nazivniku s  nadajući se da ćemo dobiti jednake kvocijente (u protivnom je naša slutnja kriva). Vrijedi nadajući se da ćemo dobiti jednake kvocijente (u protivnom je naša slutnja kriva). Vrijedi
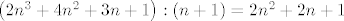 , ,
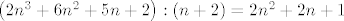 . .
Ovime smo pokazali da je
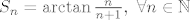 . .
Konačno,
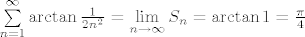 . .
|
|
| [Vrh] |
|
Tindariel
Forumaš(ica)

Pridružen/a: 03. 12. 2008. (00:49:03)
Postovi: (71)16
Spol: 
Lokacija: Zagreb
|
|
| [Vrh] |
|
Tindariel
Forumaš(ica)

Pridružen/a: 03. 12. 2008. (00:49:03)
Postovi: (71)16
Spol: 
Lokacija: Zagreb
|
|
| [Vrh] |
|
ivek imudaš
Forumaš(ica)


Pridružen/a: 13. 11. 2007. (18:41:02)
Postovi: (67)16
Spol: 
|
|
| [Vrh] |
|
|

















