| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
prove22
Forumaš(ica)

Pridružen/a: 11. 02. 2009. (18:57:32)
Postovi: (2F)16
|
|
| [Vrh] |
|
Luuka
Forumaš(ica)


Pridružen/a: 13. 02. 2007. (20:34:54)
Postovi: (925)16
Spol: 
Lokacija: Hakuna Matata
|
|
| [Vrh] |
|
prove22
Forumaš(ica)

Pridružen/a: 11. 02. 2009. (18:57:32)
Postovi: (2F)16
|
|
| [Vrh] |
|
Luuka
Forumaš(ica)


Pridružen/a: 13. 02. 2007. (20:34:54)
Postovi: (925)16
Spol: 
Lokacija: Hakuna Matata
|
 Postano: 22:21 sub, 7. 11. 2009 Naslov: Postano: 22:21 sub, 7. 11. 2009 Naslov: |
    |
|
|
ah, da FUI... Sylvester je sličan, samo s vjerojatnostima :D
Ajmo ovak, neka su:
X={brojevi manji od 1 000 000 koji nisu djeljivi ni sa 5 ni sa 7 ni sa 9}
A={brojevi manji od 1000000 djeljivi s 5}
B={brojevi manji od 1000000 djeljivi s 7}
C={brojevi manji od 1000000 djeljivi s 9}
očito je:
|A| = najveće cijelo( 1000000/5 )
|B| = najveće cijelo( 1000000/7 )
|C| = najveće cijelo( 1000000/9 )
e sad, FUI kaže ovo:
[latex] |X| = 1000000 - | AUBUC| = [/latex]
[latex]1000000 - ( |A| + |B| + |C| - |A \cap B| - |A \cap C| - |B \cap C| + |A \cap B \cap C|)[/latex]
Još samo moramo odredit koliko je brojeva koji su djeljivi i sa 5 i sa 7 (npr, za ostale analogno).
No, njih ima najveće cijelo (1000000/(5*7) )
(to su brojevi k*35, za k iz N)
Sad ćeš znat dalje :D
ah, da FUI... Sylvester je sličan, samo s vjerojatnostima 
Ajmo ovak, neka su:
X={brojevi manji od 1 000 000 koji nisu djeljivi ni sa 5 ni sa 7 ni sa 9}
A={brojevi manji od 1000000 djeljivi s 5}
B={brojevi manji od 1000000 djeljivi s 7}
C={brojevi manji od 1000000 djeljivi s 9}
očito je:
|A| = najveće cijelo( 1000000/5 )
|B| = najveće cijelo( 1000000/7 )
|C| = najveće cijelo( 1000000/9 )
e sad, FUI kaže ovo:
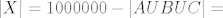
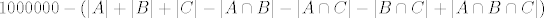
Još samo moramo odredit koliko je brojeva koji su djeljivi i sa 5 i sa 7 (npr, za ostale analogno).
No, njih ima najveće cijelo (1000000/(5*7) )
(to su brojevi k*35, za k iz N)
Sad ćeš znat dalje 
_________________ "Bolje bi prolazio na faxu da sam na drogama nego na netu" - by a friend of mine
"Poslije spavanja doma spavanje bilo di mi je najdraža stvar" - by the same guy  |
|
| [Vrh] |
|
vsego
Site Admin


Pridružen/a: 06. 10. 2002. (22:07:09)
Postovi: (3562)16
Spol: 
Lokacija: /sbin/init
|
|
| [Vrh] |
|
jejo
Forumaš(ica)

Pridružen/a: 28. 11. 2006. (19:25:36)
Postovi: (102)16
Spol: 
|
|
| [Vrh] |
|
Luuka
Forumaš(ica)


Pridružen/a: 13. 02. 2007. (20:34:54)
Postovi: (925)16
Spol: 
Lokacija: Hakuna Matata
|
|
| [Vrh] |
|
prove22
Forumaš(ica)

Pridružen/a: 11. 02. 2009. (18:57:32)
Postovi: (2F)16
|
|
| [Vrh] |
|
luzeer
Forumaš(ica)
Pridružen/a: 11. 02. 2008. (11:17:21)
Postovi: (20)16
|
|
| [Vrh] |
|
kakt00s
Forumaš(ica)


Pridružen/a: 17. 10. 2007. (12:19:40)
Postovi: (183)16
Spol: 
Lokacija: :ɐɾıɔɐʞoן
|
|
| [Vrh] |
|
daisy
Forumaš(ica)

Pridružen/a: 23. 06. 2009. (22:17:36)
Postovi: (72)16
Spol: 
|
|
| [Vrh] |
|
mery
Forumaš(ica)

Pridružen/a: 01. 12. 2008. (21:57:21)
Postovi: (43)16
|
|
| [Vrh] |
|
Saf
Forumski umjetnik


Pridružen/a: 10. 06. 2005. (21:55:28)
Postovi: (1B0)16
Spol: 
Lokacija: Zagreb
|
|
| [Vrh] |
|
Liddy
Forumaš(ica)


Pridružen/a: 17. 08. 2004. (10:03:41)
Postovi: (169)16
|
 Postano: 20:16 ned, 8. 11. 2009 Naslov: Postano: 20:16 ned, 8. 11. 2009 Naslov: |
    |
|
|
Drugi zadatak samo raspisi kako je Saf rekao, prebroji mogucnosti, a vjerojatnost ti je onda broj povoljnih (ovih kojima je zbroj 12) kroz broj mogucih (3kockice, na svakoj po 6mogucnosti {1,2,3...6}).
Ovaj broj povoljnih raspises ovako: na prvoj kocki ako ti padne 6, na drugoj 1, trecoj mora 5 da ti zbroj bude 12, pa onda opet na prvoj 6, na drugoj 2, na trecoj mora biti 4 da bi ti zbroj bio 12,pa onda 6 3 3, 6 4 2, .... mislim da ih ima 25, pa ti je onda vjerojatnost 25/216
Drugi zadatak samo raspisi kako je Saf rekao, prebroji mogucnosti, a vjerojatnost ti je onda broj povoljnih (ovih kojima je zbroj 12) kroz broj mogucih (3kockice, na svakoj po 6mogucnosti {1,2,3...6}).
Ovaj broj povoljnih raspises ovako: na prvoj kocki ako ti padne 6, na drugoj 1, trecoj mora 5 da ti zbroj bude 12, pa onda opet na prvoj 6, na drugoj 2, na trecoj mora biti 4 da bi ti zbroj bio 12,pa onda 6 3 3, 6 4 2, .... mislim da ih ima 25, pa ti je onda vjerojatnost 25/216
_________________
A man of words and not of deeds
Is like a garden full of weeds....
|
|
| [Vrh] |
|
5kyica
Forumaš(ica)

Pridružen/a: 03. 12. 2007. (16:11:37)
Postovi: (16)16
|
|
| [Vrh] |
|
Antonija
Forumaš(ica)


Pridružen/a: 04. 11. 2007. (09:38:06)
Postovi: (139)16
|
|
| [Vrh] |
|
Liddy
Forumaš(ica)


Pridružen/a: 17. 08. 2004. (10:03:41)
Postovi: (169)16
|
|
| [Vrh] |
|
5kyica
Forumaš(ica)

Pridružen/a: 03. 12. 2007. (16:11:37)
Postovi: (16)16
|
|
| [Vrh] |
|
klaudija
Forumaš(ica)
Pridružen/a: 27. 11. 2007. (22:47:50)
Postovi: (16)16
|
 Postano: 21:41 ned, 8. 11. 2009 Naslov: Postano: 21:41 ned, 8. 11. 2009 Naslov: |
    |
|
|
Može li taj zadatak preko multiskupa?
M={J1,J2,J3,J4, 2*K,7*D}
Ji- jabuke (različite)
K- kruške
D-dinje
Ukupno 13 voća
13!/(1!*1!*1!*1!*2!*7!)[/quote]
Može li taj zadatak preko multiskupa?
M={J1,J2,J3,J4, 2*K,7*D}
Ji- jabuke (različite)
K- kruške
D-dinje
Ukupno 13 voća
13!/(1!*1!*1!*1!*2!*7!)[/quote]
|
|
| [Vrh] |
|
daisy
Forumaš(ica)

Pridružen/a: 23. 06. 2009. (22:17:36)
Postovi: (72)16
Spol: 
|
 Postano: 21:47 ned, 8. 11. 2009 Naslov: Postano: 21:47 ned, 8. 11. 2009 Naslov: |
    |
|
|
ovaj sa jabukama sam rjesavala preko multiskupova...jel to onda tocno il?
a ovo s kockama, prijateljica mi je rekla da to ide kao sustav jednadzi, x1 prva kocka, x2 druga i x3 treca.. i to sve jednako 12. i onda one supstitucije s y-ima sa vjezbi.. ne znam dal je tocno, al je logicno. i da, uvjet je da je 0=<xi=<6.
ovaj sa jabukama sam rjesavala preko multiskupova...jel to onda tocno il?
a ovo s kockama, prijateljica mi je rekla da to ide kao sustav jednadzi, x1 prva kocka, x2 druga i x3 treca.. i to sve jednako 12. i onda one supstitucije s y-ima sa vjezbi.. ne znam dal je tocno, al je logicno. i da, uvjet je da je 0=<xi=<6.
|
|
| [Vrh] |
|
|













