| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
mornik
Forumaš(ica)

Pridružen/a: 26. 09. 2009. (06:25:44)
Postovi: (128)16
|
|
| [Vrh] |
|
ananas
Forumaš(ica)

Pridružen/a: 28. 10. 2009. (17:56:24)
Postovi: (34)16
|
|
| [Vrh] |
|
mornik
Forumaš(ica)

Pridružen/a: 26. 09. 2009. (06:25:44)
Postovi: (128)16
|
 Postano: 13:20 ned, 10. 1. 2010 Naslov: Postano: 13:20 ned, 10. 1. 2010 Naslov: |
    |
|
|
Da, to je jedan od onih limesa oblika [latex]f(x)^{g(x)}[/latex], pri čemu [latex]f(x)\to 1[/latex], a [latex]g(x)\to +\infty[/latex]. Tada znamo da je rješenje [latex]e[/latex] potenciran na [latex]\lim (f(x)-1)g(x)[/latex].
U našem slučaju to iznosi [latex]\displaystyle (\cos(\frac{1}{x})-1)x^2[/latex]. Sad uvedimo supstituciju [latex]\displaystyle t:=\frac{1}{x}\to 0+[/latex] (ovaj plus nam u ovom slučaju nije toliko bitan, budući da općenito postoji limes u [latex]0[/latex]). Dalje limes, dakako, znaš odrediti :).
Krajnje je rješenje, stoga, [latex]e^{-1/2}[/latex].
Da, to je jedan od onih limesa oblika 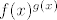 , pri čemu , pri čemu 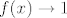 , a , a 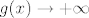 . Tada znamo da je rješenje . Tada znamo da je rješenje  potenciran na potenciran na 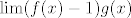 . .
U našem slučaju to iznosi 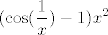 . Sad uvedimo supstituciju . Sad uvedimo supstituciju 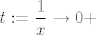 (ovaj plus nam u ovom slučaju nije toliko bitan, budući da općenito postoji limes u (ovaj plus nam u ovom slučaju nije toliko bitan, budući da općenito postoji limes u  ). Dalje limes, dakako, znaš odrediti ). Dalje limes, dakako, znaš odrediti  . .
Krajnje je rješenje, stoga, 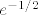 . .
|
|
| [Vrh] |
|
niveus
Forumaš(ica)

Pridružen/a: 26. 10. 2009. (16:12:58)
Postovi: (5E)16
|
|
| [Vrh] |
|
mornik
Forumaš(ica)

Pridružen/a: 26. 09. 2009. (06:25:44)
Postovi: (128)16
|
 Postano: 13:40 ned, 10. 1. 2010 Naslov: Postano: 13:40 ned, 10. 1. 2010 Naslov: |
    |
|
|
Niveus, nije meni i drugima koji tu pomažu problem pomoći, daleko od toga, ali jesi li ti to uopće pokušavala riješiti :)? Koliko se sjećam, taj zadatak se i prije pojavljivao na forumu, vjerojatno i na vježbama i zbilja nije težak. Glupo mi je sad, ne mogu dati nikakav hint na ovakav zadatak, a da ga ne riješim jer nema baš nešto puno ideja, ali molim te, daj porazmisli malo o tome što bi mogla biti ideja u zadatku pa probaj i ako ne uspiješ, nemoj odmah odustati :).
No, daklem, za sve dovoljno velike [latex]n[/latex] (pa čak i za dosta male, recimo [latex]n\geq 2[/latex] :P) vrijedi [latex]\displaystyle\frac{1}{n}\geq\frac{2}{n^2}[/latex], [latex]\displaystyle\frac{1}{n}\geq\frac{3}{n^3}[/latex] i [latex]\displaystyle\frac{1}{n}\geq\frac{4}{n^4}[/latex]. Stoga, za te "dovoljno velike" [latex]n[/latex] vrijedi [latex]\displaystyle\frac{1}{n}\leq \frac{1}{n}+\frac{2}{n^2}+\frac{3}{n^3}+\frac{4}{n^4}\leq \frac{4}{n}[/latex]. Stoga, vrijedi i [latex]\displaystyle\sqrt[n]{\frac{1}{n}}\leq \sqrt[n]{\frac{1}{n}+\frac{2}{n^2}+\frac{3}{n^3}+\frac{4}{n^4}}\leq \sqrt[n]{\frac{4}{n}}[/latex]. Budući da i lijevi i desni izraz u limesu idu u [latex]1[/latex], po teoremu o sendviču smo gotovi.
Niveus, nije meni i drugima koji tu pomažu problem pomoći, daleko od toga, ali jesi li ti to uopće pokušavala riješiti  ? Koliko se sjećam, taj zadatak se i prije pojavljivao na forumu, vjerojatno i na vježbama i zbilja nije težak. Glupo mi je sad, ne mogu dati nikakav hint na ovakav zadatak, a da ga ne riješim jer nema baš nešto puno ideja, ali molim te, daj porazmisli malo o tome što bi mogla biti ideja u zadatku pa probaj i ako ne uspiješ, nemoj odmah odustati ? Koliko se sjećam, taj zadatak se i prije pojavljivao na forumu, vjerojatno i na vježbama i zbilja nije težak. Glupo mi je sad, ne mogu dati nikakav hint na ovakav zadatak, a da ga ne riješim jer nema baš nešto puno ideja, ali molim te, daj porazmisli malo o tome što bi mogla biti ideja u zadatku pa probaj i ako ne uspiješ, nemoj odmah odustati  . .
No, daklem, za sve dovoljno velike  (pa čak i za dosta male, recimo (pa čak i za dosta male, recimo 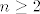  ) vrijedi ) vrijedi 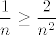 , , 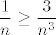 i i 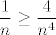 . Stoga, za te "dovoljno velike" . Stoga, za te "dovoljno velike"  vrijedi vrijedi 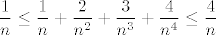 . Stoga, vrijedi i . Stoga, vrijedi i 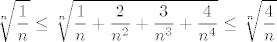 . Budući da i lijevi i desni izraz u limesu idu u . Budući da i lijevi i desni izraz u limesu idu u  , po teoremu o sendviču smo gotovi. , po teoremu o sendviču smo gotovi.
|
|
| [Vrh] |
|
suza
Forumaš(ica)

Pridružen/a: 24. 10. 2009. (14:37:50)
Postovi: (65)16
Spol: 
|
|
| [Vrh] |
|
mornik
Forumaš(ica)

Pridružen/a: 26. 09. 2009. (06:25:44)
Postovi: (128)16
|
 Postano: 14:18 ned, 10. 1. 2010 Naslov: Postano: 14:18 ned, 10. 1. 2010 Naslov: |
    |
|
|
Nema problema :).
Dakle, radi se o drugoj grupi - izvedemo, dakle, taj raspis u razliku kvadrata i dobivamo da je naš izraz jednak [latex]\displaystyle (\cosh n-\sinh n)\cdot \frac{e^{3n/2}}{\sqrt{\cosh n}+\sqrt{\sinh n}}[/latex].
U ovom trenutku ćemo samo iskoristiti da mi znamo da vrijedi [latex]\displaystyle \cosh n=\frac{e^n+e^{-n}}{2}[/latex] i [latex]\displaystyle \sinh n=\frac{e^n-e^{-n}}{2}[/latex]. Stoga mi zapravo tražimo [latex]\displaystyle \lim_{n\to +\infty} (e^{-n})\cdot \frac{e^{3n/2}}{\sqrt{\frac{e^n+e^{-n}}{2}}+\sqrt{\frac{e^n-e^{-n}}{2}}}[/latex], tj. limes od [latex]\displaystyle \frac{e^{n/2}}{\sqrt{\frac{e^n+e^{-n}}{2}}+\sqrt{\frac{e^n-e^{-n}}{2}}}[/latex]. Podijelimo sad i brojnik i nazivnik s [latex]e^{n/2}[/latex]. Dobivamo da tražimo limes od [latex]\displaystyle \frac{1}{\sqrt{\frac{1+e^{-2n}}{2}}+\sqrt{\frac{1-e^{-2n}}{2}}}[/latex], a taj limes znamo, to je [latex]\displaystyle \frac{1}{\sqrt{\frac{1}{2}}+\sqrt{\frac{1}{2}}}=\frac{\sqrt{2}}{2}[/latex].
Nema problema  . .
Dakle, radi se o drugoj grupi - izvedemo, dakle, taj raspis u razliku kvadrata i dobivamo da je naš izraz jednak 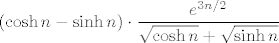 . .
U ovom trenutku ćemo samo iskoristiti da mi znamo da vrijedi 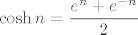 i i 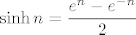 . Stoga mi zapravo tražimo . Stoga mi zapravo tražimo 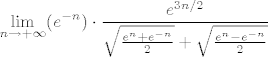 , tj. limes od , tj. limes od 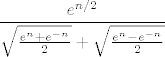 . Podijelimo sad i brojnik i nazivnik s . Podijelimo sad i brojnik i nazivnik s 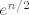 . Dobivamo da tražimo limes od . Dobivamo da tražimo limes od 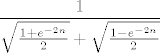 , a taj limes znamo, to je , a taj limes znamo, to je 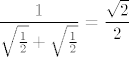 . .
|
|
| [Vrh] |
|
suza
Forumaš(ica)

Pridružen/a: 24. 10. 2009. (14:37:50)
Postovi: (65)16
Spol: 
|
|
| [Vrh] |
|
suza
Forumaš(ica)

Pridružen/a: 24. 10. 2009. (14:37:50)
Postovi: (65)16
Spol: 
|
|
| [Vrh] |
|
kaj
Forumaš(ica)

Pridružen/a: 15. 11. 2009. (21:02:20)
Postovi: (B8)16
|
|
| [Vrh] |
|
suza
Forumaš(ica)

Pridružen/a: 24. 10. 2009. (14:37:50)
Postovi: (65)16
Spol: 
|
|
| [Vrh] |
|
kaj
Forumaš(ica)

Pridružen/a: 15. 11. 2009. (21:02:20)
Postovi: (B8)16
|
|
| [Vrh] |
|
pajopatak
Forumaš(ica)

Pridružen/a: 25. 10. 2009. (22:20:04)
Postovi: (BE)16
|
|
| [Vrh] |
|
kaj
Forumaš(ica)

Pridružen/a: 15. 11. 2009. (21:02:20)
Postovi: (B8)16
|
|
| [Vrh] |
|
pajopatak
Forumaš(ica)

Pridružen/a: 25. 10. 2009. (22:20:04)
Postovi: (BE)16
|
|
| [Vrh] |
|
pmli
Forumaš(ica)

Pridružen/a: 09. 11. 2009. (12:03:05)
Postovi: (2C8)16
Spol: 
|
|
| [Vrh] |
|
kaj
Forumaš(ica)

Pridružen/a: 15. 11. 2009. (21:02:20)
Postovi: (B8)16
|
|
| [Vrh] |
|
pajopatak
Forumaš(ica)

Pridružen/a: 25. 10. 2009. (22:20:04)
Postovi: (BE)16
|
|
| [Vrh] |
|
pmli
Forumaš(ica)

Pridružen/a: 09. 11. 2009. (12:03:05)
Postovi: (2C8)16
Spol: 
|
|
| [Vrh] |
|
pajopatak
Forumaš(ica)

Pridružen/a: 25. 10. 2009. (22:20:04)
Postovi: (BE)16
|
|
| [Vrh] |
|
|










