| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
sylar
Forumaš(ica)
Pridružen/a: 13. 10. 2008. (17:42:14)
Postovi: (5F)16
|
|
| [Vrh] |
|
kenny
Petica iz zalaganja


Pridružen/a: 28. 03. 2003. (09:18:36)
Postovi: (3B7)16
Spol: 
Lokacija: ...somewhere over the rainbow...
|
|
| [Vrh] |
|
Ignavia
Forumaš(ica)


Pridružen/a: 02. 10. 2004. (19:22:39)
Postovi: (235)16
Spol: 
Lokacija: prijestolnica
|
|
| [Vrh] |
|
nitko_nezna
Forumaš(ica)

Pridružen/a: 10. 01. 2010. (15:53:34)
Postovi: (5)16
|
|
| [Vrh] |
|
lost_soul
Forumaš(ica)
Pridružen/a: 18. 10. 2009. (17:38:41)
Postovi: (133)16
|
|
| [Vrh] |
|
kenny
Petica iz zalaganja


Pridružen/a: 28. 03. 2003. (09:18:36)
Postovi: (3B7)16
Spol: 
Lokacija: ...somewhere over the rainbow...
|
 Postano: 21:06 ned, 10. 1. 2010 Naslov: Postano: 21:06 ned, 10. 1. 2010 Naslov: |
    |
|
|
Zadatak: Što je kompozicija dviju centralnih simetrija?
Prvo krenimo od ovoga: što je uopće centralna simetrija? To možemo promatrati kao kompoziciju dviju osnih simetrija, s tim da su osi simetrije međusobno okomiti.
Neka su A i B centri simetrije. Te dvije točke određuju pravac c. U točkama A i B "dignimo" okomice na c i nazovimo ih pravcima a i b.
Sad možemo pisati: [latex]s_c \circ s_a = s_A, s_b \circ s_c = s_B[/latex].
NAPOMENA: mogli smo ove kompozicije napisati i obrnuto: [latex]s_a \circ s_c = s_A, s_c \circ s_b = s_B[/latex] jer je kompozicija dviju osnih simetrija komutativna ako su osi simetrije okomiti pravci.
Nas sada zanima što je kompozicija tih dviju centralnih simetrija.
[latex]s_B \circ s_A = s_b \circ s_c \circ s_c \circ s_a[/latex].
Kako je osna simetrija involutorno preslikavanje, odnosno vrijedi [latex]s_c \circ s_c = i[/latex] možemo pisati:
[latex]s_B \circ s_A = s_b \circ s_a[/latex].
Dakle, dobili smo da je kompozicija dviju centralnih simetrija ujedno i kompozicija dviju osnih simetrija. Još ima jedan ključni dio: te dvije osne simetrije imaju paralelne pravce (to zaključujemo jer su obje osi simetrije okomite na spojnicu točaka A i B), pa konačno zaključujemo: kompozicija dviju centralnih simetrija je TRANSLACIJA za vektor [latex]2 \vec{AB}[/latex]. gdje su točke A i B zadani centri simetrija.
Zadatak: Što je kompozicija dviju centralnih simetrija?
Prvo krenimo od ovoga: što je uopće centralna simetrija? To možemo promatrati kao kompoziciju dviju osnih simetrija, s tim da su osi simetrije međusobno okomiti.
Neka su A i B centri simetrije. Te dvije točke određuju pravac c. U točkama A i B "dignimo" okomice na c i nazovimo ih pravcima a i b.
Sad možemo pisati: 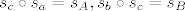 . .
NAPOMENA: mogli smo ove kompozicije napisati i obrnuto: 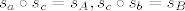 jer je kompozicija dviju osnih simetrija komutativna ako su osi simetrije okomiti pravci. jer je kompozicija dviju osnih simetrija komutativna ako su osi simetrije okomiti pravci.
Nas sada zanima što je kompozicija tih dviju centralnih simetrija.
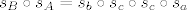 . .
Kako je osna simetrija involutorno preslikavanje, odnosno vrijedi 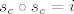 možemo pisati: možemo pisati:
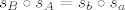 . .
Dakle, dobili smo da je kompozicija dviju centralnih simetrija ujedno i kompozicija dviju osnih simetrija. Još ima jedan ključni dio: te dvije osne simetrije imaju paralelne pravce (to zaključujemo jer su obje osi simetrije okomite na spojnicu točaka A i B), pa konačno zaključujemo: kompozicija dviju centralnih simetrija je TRANSLACIJA za vektor 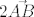 . gdje su točke A i B zadani centri simetrija. . gdje su točke A i B zadani centri simetrija.
_________________
Dvije stvari su beskonacne: svemir i ljudska glupost. Za ono prvo nisam siguran.
by A.Einstein
|
|
| [Vrh] |
|
lost_soul
Forumaš(ica)
Pridružen/a: 18. 10. 2009. (17:38:41)
Postovi: (133)16
|
|
| [Vrh] |
|
teapot
Forumaš(ica)
Pridružen/a: 12. 02. 2009. (22:01:19)
Postovi: (36)16
|
|
| [Vrh] |
|
kenny
Petica iz zalaganja


Pridružen/a: 28. 03. 2003. (09:18:36)
Postovi: (3B7)16
Spol: 
Lokacija: ...somewhere over the rainbow...
|
 Postano: 4:13 pon, 11. 1. 2010 Naslov: Postano: 4:13 pon, 11. 1. 2010 Naslov: |
    |
|
|
16. zadatak:
Prvo se podsjetimo što je potencija točke na danu kružnicu. Neka je dana neka kružnica k i proizvoljna točka T koja nije na kružnici. Povucimo točkom T bilo koji pravac koji siječe kružnicu k u točkama A i B. Realan broj [latex]|TA| \cdot |TB|[/latex] zove se potencija točke T na kružnicu k.
Idemo sada pogledati zadatak. Veli da se kružnice sijeku u točkama A i B i da je na pravcu određenom tim točkama uzeta neka točka T. Računamo prvo potenciju za prvu kružnicu:
[latex]p_1 = |TA| \cdot |TB|, A, B \in k_1[/latex]
I onda za drugu kružnicu:
[latex]p_2 = |TA| \cdot |TB|, A, B \in k_2[/latex].
Vidimo da su potencije jednake. ;)
Basicly, zadatak veli ovo: dane su dvije kružnice koje se sijeku. Geometrijsko mjesto točaka koje imaju jednaku potenciju s obzirom na obje kružnice je na pravcu koji je određen sjecištima tih kružnica.
[size=9][color=#999999]Added after 18 minutes:[/color][/size]
11. zadatak (kad ste već toliko zapeli za njega):
Nadao sam se da ćete gledajući onaj zadatak koji sam prije rješio (o kompoziciju dviju osnih simetrija) shvatiti rješenje ovog zadatka.
Neka je dan pravac [latex]p[/latex] i točka na tom pravcu [latex]T \in p[/latex]. Treba vidjeti da osna simetrija i centralna simetrija sa zadanim elementima komutiraju.
U točki [latex]T[/latex] konstruirajmo pravac [latex]t[/latex] koji je okomit na dani pravac [latex]p[/latex].
Centralnu simetriju možemo napisati kao kompoziciju dviju osnih simetrija čije su osi međusobno okomite (ta kompozicija komutira!): [latex]s_T = s_p \circ s_t = s_t \circ \s_p[/latex].
Pogledajmo sada komutiraju li zadana osna i centralna simetrija:
[latex]s_p \circ s_T = s_p \circ s_p \circ s_t = s_t \\
s_T \circ s_p = s_t \circ s_p \circ s_p = s_t \\
s_T \circ s_p = s_p \circ s_T[/latex]
Dakle, zaključak je: da, osna i centralna simetrija komutiraju ukoliko je centar simetrije na osi simetrije. U tom je slučaju kompozicija tih simetrija jednaka osnoj simetriji s obzirom na pravac koji je okomit na početnu os simetrije, a prolazi danom točkom.
NAPOMENA: ako nije jasno gdje nam se gore izgubila osna simetrija....osna simetrija je involutorno preslikavanje, odnosno dvostrukom primjenom tog preslikavanja dobije se identiteta...odnosno: [latex]s_p \circ s_p = i[/latex]
16. zadatak:
Prvo se podsjetimo što je potencija točke na danu kružnicu. Neka je dana neka kružnica k i proizvoljna točka T koja nije na kružnici. Povucimo točkom T bilo koji pravac koji siječe kružnicu k u točkama A i B. Realan broj  zove se potencija točke T na kružnicu k. zove se potencija točke T na kružnicu k.
Idemo sada pogledati zadatak. Veli da se kružnice sijeku u točkama A i B i da je na pravcu određenom tim točkama uzeta neka točka T. Računamo prvo potenciju za prvu kružnicu:
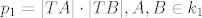
I onda za drugu kružnicu:
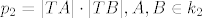 . .
Vidimo da su potencije jednake. 
Basicly, zadatak veli ovo: dane su dvije kružnice koje se sijeku. Geometrijsko mjesto točaka koje imaju jednaku potenciju s obzirom na obje kružnice je na pravcu koji je određen sjecištima tih kružnica.
Added after 18 minutes:
11. zadatak (kad ste već toliko zapeli za njega):
Nadao sam se da ćete gledajući onaj zadatak koji sam prije rješio (o kompoziciju dviju osnih simetrija) shvatiti rješenje ovog zadatka.
Neka je dan pravac  i točka na tom pravcu i točka na tom pravcu 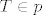 . Treba vidjeti da osna simetrija i centralna simetrija sa zadanim elementima komutiraju. . Treba vidjeti da osna simetrija i centralna simetrija sa zadanim elementima komutiraju.
U točki  konstruirajmo pravac konstruirajmo pravac  koji je okomit na dani pravac koji je okomit na dani pravac  . .
Centralnu simetriju možemo napisati kao kompoziciju dviju osnih simetrija čije su osi međusobno okomite (ta kompozicija komutira!): 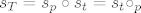 . .
Pogledajmo sada komutiraju li zadana osna i centralna simetrija:
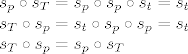
Dakle, zaključak je: da, osna i centralna simetrija komutiraju ukoliko je centar simetrije na osi simetrije. U tom je slučaju kompozicija tih simetrija jednaka osnoj simetriji s obzirom na pravac koji je okomit na početnu os simetrije, a prolazi danom točkom.
NAPOMENA: ako nije jasno gdje nam se gore izgubila osna simetrija....osna simetrija je involutorno preslikavanje, odnosno dvostrukom primjenom tog preslikavanja dobije se identiteta...odnosno: 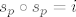
_________________
Dvije stvari su beskonacne: svemir i ljudska glupost. Za ono prvo nisam siguran.
by A.Einstein
|
|
| [Vrh] |
|
world_traveler
Forumaš(ica)

Pridružen/a: 24. 09. 2009. (14:43:09)
Postovi: (14)16
Spol: 
|
|
| [Vrh] |
|
mawa
Forumaš(ica)

Pridružen/a: 11. 10. 2009. (13:18:04)
Postovi: (13)16
Spol: 
|
|
| [Vrh] |
|
BeeBee
Forumaš(ica)

Pridružen/a: 08. 11. 2009. (16:07:39)
Postovi: (79)16
|
|
| [Vrh] |
|
Serious Sam
Forumaš(ica)


Pridružen/a: 09. 12. 2009. (15:08:32)
Postovi: (5C)16
Spol: 
|
|
| [Vrh] |
|
domokun
Forumaš(ica)


Pridružen/a: 15. 01. 2009. (22:49:41)
Postovi: (1F)16
Spol: 
|
|
| [Vrh] |
|
mawa
Forumaš(ica)

Pridružen/a: 11. 10. 2009. (13:18:04)
Postovi: (13)16
Spol: 
|
|
| [Vrh] |
|
lost_soul
Forumaš(ica)
Pridružen/a: 18. 10. 2009. (17:38:41)
Postovi: (133)16
|
|
| [Vrh] |
|
BeeBee
Forumaš(ica)

Pridružen/a: 08. 11. 2009. (16:07:39)
Postovi: (79)16
|
|
| [Vrh] |
|
kenny
Petica iz zalaganja


Pridružen/a: 28. 03. 2003. (09:18:36)
Postovi: (3B7)16
Spol: 
Lokacija: ...somewhere over the rainbow...
|
 Postano: 14:49 pon, 11. 1. 2010 Naslov: Postano: 14:49 pon, 11. 1. 2010 Naslov: |
    |
|
|
Hm, prvo moram napomenuti da sam ja ovo položio jako davno i nisam siguran koliko ste vi radili toga na ovom kolegiju. Napominjem jer ću u rješavanju koristiti neke stvari koje neću dokazivati... Ako bude trebalo još to dokazivati, vičite, pa vam i to raspišem.
[b]Zadatak 6 (kompozicija dviju translacija):[/b]
Za početak - translaciju možemo zapisati kao kompoziciju dviju osnih simetrija [latex]s_b \circ s_a[/latex] za koje vrijedi da su osi simetrije paralelni pravci.
E sad, neka su zadane dvije translacije: [latex]s_b \circ s_a, s_d \circ s_c[/latex]. Uzmimo točku [latex]A[/latex] po volji. U zadatku o kompoziciju dviju centralnih simetrija se dokazalo da je kompozicija dviju osnih simetrija ujedno i kompozicija dviju centralnih simetrija (uvažavajući činjenicu da te dvije osne simetrije imaju paralelne osi simetrije i da su centri centralnih simetrija sjecišta pravca okomitog na osi osne simetrije). Iz toga slijedi da [latex]\exists B s_b \circ s_a = s_B \circ s_A[/latex]. Uzmimo sada tu točku [latex]B[/latex] i na nju opet primjenimo isti zaključak: [latex]\exists C s_d \circ s_c = s_C \circ s_B[/latex].
Zanima nas kompozicija translacija: [latex]s_d \circ s_c \circ s_b \circ s_a = s_C \circ s_B \circ s_B \circ s_A = s_C \circ s_A[/latex]. A znamo (u nekom prije zadatku sam dokazao): kompozicija dviju centralnih simetrija je translacija.
[b]ZAKLJUČAK:[/b] kompozicija dviju translacija je TRANSLACIJA.
Hm, prvo moram napomenuti da sam ja ovo položio jako davno i nisam siguran koliko ste vi radili toga na ovom kolegiju. Napominjem jer ću u rješavanju koristiti neke stvari koje neću dokazivati... Ako bude trebalo još to dokazivati, vičite, pa vam i to raspišem.
Zadatak 6 (kompozicija dviju translacija):
Za početak - translaciju možemo zapisati kao kompoziciju dviju osnih simetrija 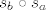 za koje vrijedi da su osi simetrije paralelni pravci. za koje vrijedi da su osi simetrije paralelni pravci.
E sad, neka su zadane dvije translacije: 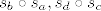 . Uzmimo točku . Uzmimo točku  po volji. U zadatku o kompoziciju dviju centralnih simetrija se dokazalo da je kompozicija dviju osnih simetrija ujedno i kompozicija dviju centralnih simetrija (uvažavajući činjenicu da te dvije osne simetrije imaju paralelne osi simetrije i da su centri centralnih simetrija sjecišta pravca okomitog na osi osne simetrije). Iz toga slijedi da po volji. U zadatku o kompoziciju dviju centralnih simetrija se dokazalo da je kompozicija dviju osnih simetrija ujedno i kompozicija dviju centralnih simetrija (uvažavajući činjenicu da te dvije osne simetrije imaju paralelne osi simetrije i da su centri centralnih simetrija sjecišta pravca okomitog na osi osne simetrije). Iz toga slijedi da 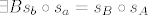 . Uzmimo sada tu točku . Uzmimo sada tu točku  i na nju opet primjenimo isti zaključak: i na nju opet primjenimo isti zaključak: 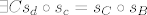 . .
Zanima nas kompozicija translacija: 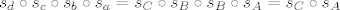 . A znamo (u nekom prije zadatku sam dokazao): kompozicija dviju centralnih simetrija je translacija. . A znamo (u nekom prije zadatku sam dokazao): kompozicija dviju centralnih simetrija je translacija.
ZAKLJUČAK: kompozicija dviju translacija je TRANSLACIJA.
_________________
Dvije stvari su beskonacne: svemir i ljudska glupost. Za ono prvo nisam siguran.
by A.Einstein
|
|
| [Vrh] |
|
teapot
Forumaš(ica)
Pridružen/a: 12. 02. 2009. (22:01:19)
Postovi: (36)16
|
|
| [Vrh] |
|
mawa
Forumaš(ica)

Pridružen/a: 11. 10. 2009. (13:18:04)
Postovi: (13)16
Spol: 
|
|
| [Vrh] |
|
|















