| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
čungalunga
Forumaš(ica)


Pridružen/a: 25. 11. 2009. (20:50:12)
Postovi: (4C)16
Spol: 
Lokacija: varaždin/zagreb
|
|
| [Vrh] |
|
Milojko
Forumaš(ica)


Pridružen/a: 07. 11. 2008. (14:57:52)
Postovi: (453)16
Spol: 
Lokacija: Hilbertov hotel
|
 Postano: 16:41 uto, 19. 1. 2010 Naslov: Postano: 16:41 uto, 19. 1. 2010 Naslov: |
    |
|
|
X = B (100, 1/50) lambda = 2, P (X >= 3) = 1 - P (X <= 2)
X = B (100, 1/50) lambda = 2, P (X >= 3) = 1 - P (X <= 2)
_________________ Sedam je prost broj 
Bolonja je smeće i to pod hitno treba mijenjat |
|
| [Vrh] |
|
.anchy.
Forumaš(ica)

Pridružen/a: 14. 11. 2007. (20:03:46)
Postovi: (1BC)16
Lokacija: Zgb
|
|
| [Vrh] |
|
Sphiro
Forumaš(ica)
Pridružen/a: 17. 10. 2007. (16:32:45)
Postovi: (45)16
|
|
| [Vrh] |
|
šišmiš
Forumaš(ica)

Pridružen/a: 19. 04. 2010. (21:01:19)
Postovi: (29)16
|
|
| [Vrh] |
|
ankovacic
Forumaš(ica)

Pridružen/a: 27. 10. 2009. (19:28:17)
Postovi: (5C)16
Spol: 
|
 Postano: 13:46 sub, 15. 1. 2011 Naslov: Postano: 13:46 sub, 15. 1. 2011 Naslov: |
    |
|
|
3.16.
Očigledno je da je [latex]\vert \Omega \vert = \vert \{(a, b, c),\colon a,b,c \in \{1,2,3,4,5,6\}\} \vert =6^3[/latex]
A={najveći dobiveni broj je barem 2* veći od najmanjeg dobivenog broja}
[latex]\vert A^c \vert[/latex] =|{najveći dobiveni broj ne smije biti 2* veći od najmanjeg dobivenog broja}|=|{zbroj permutacija ovih multiskupova [latex]\{1^3\},\{2^3\}, \{3^3\},\{4^3\}, \{5^3\}, \{6^3\},\{2^2, 3\}, \{3^2, 2\}, \{3, 4^2\}, \{4, 3^2\}, \{5^2, 3\}, [/latex] [latex] \{3^2, 5\}, \{3, 4, 5\}, \{4^2, 5\}, \{5^2, 4\}, \{4^2, 6\}, \{6^2, 4\}, \{5^2, 6\}, \{6^2, 5\}, \{4,5,6\}\} \vert =6+3*12+2*6=54[/latex]
[latex]P(A)=1-P(A^c)=1-54/(6^3)=0.75[/latex]
3.18 ne znam
3.19
[latex]\vert \Omega \vert = \vert \{ (x_1,...,x_5), \colon za \\ i \neq j , x_i \neq x_j, x_i \in \{ 1,2,..., 20 \}\} \vert = 20*19*18*17*16[/latex]=
a)
A={brojevi moraju biti uzastopni}={izaberemo koji je najmanji broj, takvih može biti 16, (time smo izabrali i ostala 4) i još ih ispermutiramo}
kard (A)=16*5!
P(A)=16*5! /(20*19*18*17*16)
b)
B={brojevi moraju biti uzastopni, ali tako da su izvučeni u pravilnom redoslijedu}={izaberemo koji je najmanji broj, a takvih može biti 16}
kard(B)=16
P(B)=16/(20*19*18*17*16)
3.21
[latex]\vert \Omega \vert = \vert \{1,2,3,4,5,6 \}^n \vert =6^n [/latex]
A={barem se jednom pojavila 1}
P(A)>=0.99, a to je ekvivalentno tome da je
P(A^c)<0.01, ekvival. tome
(5/6)^n < 0.01 a to je onda kada je n<25,
A to ti je n za koji se jedinica neće pojaviti ni jednom s vjerojatnošću od 0.01, ti trebaš da se pojavi barem jednom s vjer. od 0.99 a to ti je onda za n>=25.
3.16.
Očigledno je da je 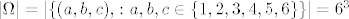
A={najveći dobiveni broj je barem 2* veći od najmanjeg dobivenog broja}
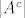 =|{najveći dobiveni broj ne smije biti 2* veći od najmanjeg dobivenog broja}|=|{zbroj permutacija ovih multiskupova =|{najveći dobiveni broj ne smije biti 2* veći od najmanjeg dobivenog broja}|=|{zbroj permutacija ovih multiskupova 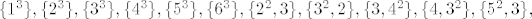 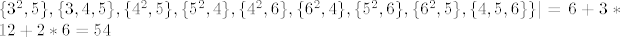
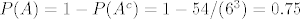
3.18 ne znam
3.19
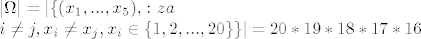 = =
a)
A={brojevi moraju biti uzastopni}={izaberemo koji je najmanji broj, takvih može biti 16, (time smo izabrali i ostala 4) i još ih ispermutiramo}
kard (A)=16*5!
P(A)=16*5! /(20*19*18*17*16)
b)
B={brojevi moraju biti uzastopni, ali tako da su izvučeni u pravilnom redoslijedu}={izaberemo koji je najmanji broj, a takvih može biti 16}
kard(B)=16
P(B)=16/(20*19*18*17*16)
3.21
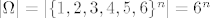
A={barem se jednom pojavila 1}
P(A)>=0.99, a to je ekvivalentno tome da je
P(A^c)<0.01, ekvival. tome
(5/6)^n < 0.01 a to je onda kada je n<25,
A to ti je n za koji se jedinica neće pojaviti ni jednom s vjerojatnošću od 0.01, ti trebaš da se pojavi barem jednom s vjer. od 0.99 a to ti je onda za n>=25.
|
|
| [Vrh] |
|
šišmiš
Forumaš(ica)

Pridružen/a: 19. 04. 2010. (21:01:19)
Postovi: (29)16
|
|
| [Vrh] |
|
lanek
Forumaš(ica)


Pridružen/a: 06. 10. 2009. (21:51:48)
Postovi: (51)16
Spol: 
|
|
| [Vrh] |
|
eve
Forumaš(ica)

Pridružen/a: 13. 07. 2009. (23:07:06)
Postovi: (192)16
Spol: 
|
|
| [Vrh] |
|
lanek
Forumaš(ica)


Pridružen/a: 06. 10. 2009. (21:51:48)
Postovi: (51)16
Spol: 
|
|
| [Vrh] |
|
eve
Forumaš(ica)

Pridružen/a: 13. 07. 2009. (23:07:06)
Postovi: (192)16
Spol: 
|
|
| [Vrh] |
|
kaj
Forumaš(ica)

Pridružen/a: 15. 11. 2009. (21:02:20)
Postovi: (B8)16
|
|
| [Vrh] |
|
ante c
Forumaš(ica)


Pridružen/a: 10. 10. 2009. (19:18:15)
Postovi: (62)16
|
|
| [Vrh] |
|
andra
Forumaš(ica)

Pridružen/a: 02. 11. 2009. (19:23:23)
Postovi: (4F)16
|
|
| [Vrh] |
|
some_dude
Forumaš(ica)
Pridružen/a: 08. 11. 2009. (16:23:13)
Postovi: (59)16
Spol: 
Lokacija: Zd-Zg
|
|
| [Vrh] |
|
patlidzan
Forumaš(ica)

Pridružen/a: 05. 11. 2009. (19:17:28)
Postovi: (76)16
Spol: 
|
|
| [Vrh] |
|
pmli
Forumaš(ica)

Pridružen/a: 09. 11. 2009. (12:03:05)
Postovi: (2C8)16
Spol: 
|
 Postano: 22:20 pon, 31. 1. 2011 Naslov: Postano: 22:20 pon, 31. 1. 2011 Naslov: |
    |
|
|
1.37 [latex]\mathbb{P}(\{c\}) = \mathbb{P}(\{a, b, c\}) - \mathbb{P}(\{a, b\})[/latex], [latex]\mathbb{P}(\{a\}) = \mathbb{P}(\{a, b, c\}) - \mathbb{P}(\{b, c\})[/latex], [latex]\mathbb{P}(\{b\}) = \mathbb{P}(\{a, b, c\}) - \mathbb{P}(\{a\}) - \mathbb{P}(\{c\})[/latex]
1.48 A = {zbroj u jednom bacanju je 5}, B = {zbroj u jednom bacanju je 7}, [latex]\displaystyle \mathbb{P}(A) = \frac{4}{36} = \frac{1}{9}[/latex], [latex]\displaystyle \mathbb{P}(B) = \frac{6}{36} = \frac{1}{6}[/latex], [latex]\displaystyle \mathbb{P}(A^{\complement} \cap B^{\complement}) = \frac{13}{18}[/latex].
[latex]C_n[/latex]= {u [latex]n[/latex] bacanja, u zadnjem je zbroj je 5, a u preostalima različito od 5 i 7}, [latex]\displaystyle \mathbb{P}(C_n) = \left( \frac{13}{18} \right)^{n - 1} \frac{1}{9}[/latex].
[latex]\displaystyle \mathbb{P}\left( \bigcup_{n = 1}^{\infty} C_n \right) = \sum_{n = 1}^{\infty} \left( \frac{13}{18} \right)^{n - 1} \frac{1}{9} = \frac{2}{5}[/latex]
1.51 Iskoristi 1.46
1.52 Radilo se na predavanju i na vježbama. Za [latex]n[/latex] bacanja, vjerojatnost da niti jednom ne padne dvostruka šestica jest [latex]\displaystyle \left( \frac{35}{36} \right)^n[/latex].
1.37 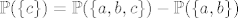 , , 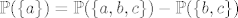 , , 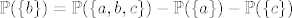
1.48 A = {zbroj u jednom bacanju je 5}, B = {zbroj u jednom bacanju je 7}, 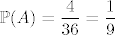 , , 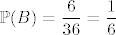 , , 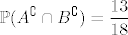 . .
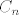 = {u = {u  bacanja, u zadnjem je zbroj je 5, a u preostalima različito od 5 i 7}, bacanja, u zadnjem je zbroj je 5, a u preostalima različito od 5 i 7}, 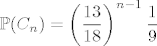 . .
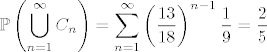
1.51 Iskoristi 1.46
1.52 Radilo se na predavanju i na vježbama. Za  bacanja, vjerojatnost da niti jednom ne padne dvostruka šestica jest bacanja, vjerojatnost da niti jednom ne padne dvostruka šestica jest 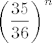 . .
|
|
| [Vrh] |
|
ananas
Forumaš(ica)

Pridružen/a: 28. 10. 2009. (17:56:24)
Postovi: (34)16
|
|
| [Vrh] |
|
some_dude
Forumaš(ica)
Pridružen/a: 08. 11. 2009. (16:23:13)
Postovi: (59)16
Spol: 
Lokacija: Zd-Zg
|
|
| [Vrh] |
|
ananas
Forumaš(ica)

Pridružen/a: 28. 10. 2009. (17:56:24)
Postovi: (34)16
|
|
| [Vrh] |
|
|















