| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
rose
Forumaš(ica)

Pridružen/a: 16. 12. 2005. (22:16:57)
Postovi: (7)16
|
|
| [Vrh] |
|
rose
Forumaš(ica)

Pridružen/a: 16. 12. 2005. (22:16:57)
Postovi: (7)16
|
|
| [Vrh] |
|
rose
Forumaš(ica)

Pridružen/a: 16. 12. 2005. (22:16:57)
Postovi: (7)16
|
|
| [Vrh] |
|
rafaelm
Forumaš(ica)


Pridružen/a: 24. 12. 2006. (13:30:11)
Postovi: (21F)16
Spol: 
Lokacija: Zagreb
|
|
| [Vrh] |
|
rafaelm
Forumaš(ica)


Pridružen/a: 24. 12. 2006. (13:30:11)
Postovi: (21F)16
Spol: 
Lokacija: Zagreb
|
|
| [Vrh] |
|
rafaelm
Forumaš(ica)


Pridružen/a: 24. 12. 2006. (13:30:11)
Postovi: (21F)16
Spol: 
Lokacija: Zagreb
|
|
| [Vrh] |
|
rafaelm
Forumaš(ica)


Pridružen/a: 24. 12. 2006. (13:30:11)
Postovi: (21F)16
Spol: 
Lokacija: Zagreb
|
 Postano: 16:32 pet, 21. 5. 2010 Naslov: Postano: 16:32 pet, 21. 5. 2010 Naslov: |
    |
|
|
[quote="rafaelm"]Od sljedećeg tjedna, zbog promjene rasporeda moje demonstrature se održavaju petkom, 17-19, u praktikumu 4.[/quote]
Sljedeći tjedan (zadnji) demonstrature će se održati u utorak, 17-19h, u praktikumu 4.
Ispričavam se zbog stalnih promjena. Postoji mogućnost dogovora mailom oko drugog termina ako netko treba.
| rafaelm (napisa): | | Od sljedećeg tjedna, zbog promjene rasporeda moje demonstrature se održavaju petkom, 17-19, u praktikumu 4. |
Sljedeći tjedan (zadnji) demonstrature će se održati u utorak, 17-19h, u praktikumu 4.
Ispričavam se zbog stalnih promjena. Postoji mogućnost dogovora mailom oko drugog termina ako netko treba.
|
|
| [Vrh] |
|
Novi
Forumaš(ica)

Pridružen/a: 17. 07. 2007. (12:08:32)
Postovi: (11F)16
Spol: 
|
|
| [Vrh] |
|
Novi
Forumaš(ica)

Pridružen/a: 17. 07. 2007. (12:08:32)
Postovi: (11F)16
Spol: 
|
|
| [Vrh] |
|
Novi
Forumaš(ica)

Pridružen/a: 17. 07. 2007. (12:08:32)
Postovi: (11F)16
Spol: 
|
 Postano: 15:51 čet, 26. 5. 2011 Naslov: Današnje demonstrature Postano: 15:51 čet, 26. 5. 2011 Naslov: Današnje demonstrature |
    |
|
|
Evo detaljnog raspisa zadatka broj 2 od [url=http://sites.google.com/site/mathnastava/home/teorija-skupova/rezultatipopravnogkolokvija/TS.s3z.10-05-27.pdf]ovdje[/url] koji sam ostao dužan. Možda još nekim ljudima ovo bude korisno :)
(a) Vrijedi [latex]\omega^\omega \leq \omega^\omega +1[/latex] pa je [latex]\omega^\omega\omega=\omega^{\omega+1} \leq (\omega^\omega +1)\omega[/latex]. Obratno računamo, [latex](\omega^\omega +1)\omega=\sup_{n\in\omega}\{(\omega^\omega +1)n\}=\sup_{n\in\omega}\{\omega^\omega n +1\}[/latex]. Sada za sve [latex]n\in\omega[/latex] vrijedi [latex]\omega^\omega n +1 \leq \omega^\omega n +\omega^\omega = \omega^\omega (n+1) \leq \omega^\omega \omega = \omega^{\omega+1}[/latex] pa kad lupim supremum dobijem i drugu nejednakost čime je (a) dio dokazan.
(b) Prvo uočimo [latex]5\omega=\sup_{n\in\omega}\{5n\}=\omega[/latex] i isto [latex]2\omega^\omega=2\omega^{1+\omega}=2\omega\omega^\omega=\omega\omega^\omega=\omega^{1+\omega}=\omega^\omega[/latex]. Dakle treba izračunati [latex](\omega^\omega+\omega)^3[/latex]. Idemo sve polako redom. Prvo kvadrat [latex](\omega^\omega+\omega)^2=(\omega^\omega+\omega)\omega^\omega+(\omega^\omega+\omega)\omega=(\omega^\omega+\omega)\omega^{1+\omega}+(\omega^\omega+\omega)\omega=[/latex][latex](\omega^\omega+\omega)\omega\omega^\omega+(\omega^\omega+\omega)\omega[/latex]. Dakle dovoljno je izracunati [latex](\omega^\omega+\omega)\omega[/latex], za što se sličnim računom kao u (a) dobije da je isto [latex]\omega^{\omega+1}[/latex]. Konačno, [latex](\omega^\omega+\omega)^3=(\omega^{\omega 2}+\omega^{\omega +1})(\omega^\omega+\omega)=\cdots=[/latex]slično kao i gore se računa i dobije se[latex]=\cdots=\omega^{\omega 3}+\omega^{\omega 2 +1}[/latex]
Što se tiče šestog zadatka, druga grupa od [url=http://web.math.hr/~veky/B/TS.k2z.08-07-02.pdf]ovdje[/url], ono što sam rekao je u redu. Dakle istina je da ispada da u promatranoj familiji nema ništa osim prazne familije podskupova, pa onda trivijalno taj jedini element PUSa jest maksimalan.
Eto, valjda nisam što zbrljavio.
Zahvale Ani, Jeleni i Mariju, bez čije pomoći ne bi bilo ovog posta :P
[size=7]Sad još samo da netko stavi rješenje u dvije crte, i moj blam će biti potpun :oops: [/size]
Evo detaljnog raspisa zadatka broj 2 od ovdje koji sam ostao dužan. Možda još nekim ljudima ovo bude korisno 
(a) Vrijedi 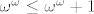 pa je pa je 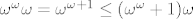 . Obratno računamo, . Obratno računamo,  . Sada za sve . Sada za sve 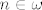 vrijedi vrijedi 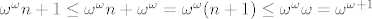 pa kad lupim supremum dobijem i drugu nejednakost čime je (a) dio dokazan. pa kad lupim supremum dobijem i drugu nejednakost čime je (a) dio dokazan.
(b) Prvo uočimo 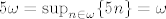 i isto i isto 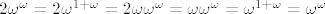 . Dakle treba izračunati . Dakle treba izračunati  . Idemo sve polako redom. Prvo kvadrat . Idemo sve polako redom. Prvo kvadrat 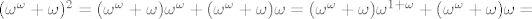 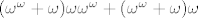 . Dakle dovoljno je izracunati . Dakle dovoljno je izracunati  , za što se sličnim računom kao u (a) dobije da je isto , za što se sličnim računom kao u (a) dobije da je isto 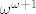 . Konačno, . Konačno, 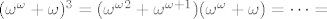 slično kao i gore se računa i dobije se slično kao i gore se računa i dobije se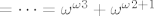
Što se tiče šestog zadatka, druga grupa od ovdje, ono što sam rekao je u redu. Dakle istina je da ispada da u promatranoj familiji nema ništa osim prazne familije podskupova, pa onda trivijalno taj jedini element PUSa jest maksimalan.
Eto, valjda nisam što zbrljavio.
Zahvale Ani, Jeleni i Mariju, bez čije pomoći ne bi bilo ovog posta 
Sad još samo da netko stavi rješenje u dvije crte, i moj blam će biti potpun 
_________________
Jedan je smjer očit, a drugi je trivijalan.
|
|
| [Vrh] |
|
|











