| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
ivicasb1
Forumaš(ica)

Pridružen/a: 17. 04. 2009. (16:56:50)
Postovi: (5D)16
|
|
| [Vrh] |
|
ivicasb1
Forumaš(ica)

Pridružen/a: 17. 04. 2009. (16:56:50)
Postovi: (5D)16
|
|
| [Vrh] |
|
Swerz
Forumaš(ica)


Pridružen/a: 13. 02. 2009. (21:30:28)
Postovi: (182)16
Spol: 
|
 Postano: 14:06 sri, 24. 2. 2010 Naslov: Postano: 14:06 sri, 24. 2. 2010 Naslov: |
    |
|
|
[quote="ovdje sam sfušao brojke al neka ostane"]Ajmo prvo probati sa hintom pa ak neide netko ce ti dati cijeli postupak.
tj. si ziher da je tu [b]cos[/b] a ne mozda [b]sin[/b]?
U oba slucaja ideja ti je sljedeca...
[b]n[/b] moze biti paran ili neparan. Dakle radis 2 slucaja jedan za parne a drugi za neparne.
Te sinuse i kosinuse stavljaju tu upravo zbog tih predznaka jer ide od -1 do +1 i u pravilu to im je jedina svrha.
Ajmo sad na zadatak.
Ak si dobro prepisao zadatak onda je niz trivijalan i ima samo jedan član {1}. Uvrsti pa ces vidjeti
Ak si krivo prepisao zadatak onda za parne n-ove niz je rastuc, i odozdo omeđen sa [latex]\frac{3}{2}[/latex] koji je ujedno i minimum jer se postiže a supremum je limes niza ilitiga [latex]2[/latex] i on se ne postize pa stoga nije max.
Za neparne n-ove, niz je padajuc i odozgo omeđen sa [latex]\frac{1}{3}[/latex] koji je ujedno i max. Infimum je limes ilitiga [latex]0[/latex] i on nije min jer se ne postiže.
inf = min{[latex]0[/latex], [latex]\frac{3}{2}[/latex]} = [latex]0[/latex]
sup = max{[latex]2[/latex], [latex]\frac{1}{3}[/latex]}
Uoci da se ne postize ni inf niti sup pa nema niti min niti max.
To bi bilo to, nadam se da nisam napravio pacersku pogrešku...[/quote]
EDIT: evo pacerske pogreske, bum je ispravio...
EDIT2: pacerska pogreska je bila kaj nisam procitao cijeli thread i sad pretpostavljam da si ipak dobro napisao zadatak.
Prica i objasnjenja su ista kao i prije ovog edita al samo sa drugim brojkama.
Za neparne n-ove niz je trivijalnog oblika {1} dakle sup=max=inf=min=[latex]1[/latex]
za parne n-ove niz je odozdo omeđen sa [latex]0[/latex] a odozgo sa [latex]2[/latex] i oni se ne postizu.
Dakle inf niza je [b]0[/b] a supremum [b]2[/b] i oni se ne postižu.
Valjda sam ovaj put dobro rijesio :roll:
| ovdje sam sfušao brojke al neka ostane (napisa): | Ajmo prvo probati sa hintom pa ak neide netko ce ti dati cijeli postupak.
tj. si ziher da je tu cos a ne mozda sin?
U oba slucaja ideja ti je sljedeca...
n moze biti paran ili neparan. Dakle radis 2 slucaja jedan za parne a drugi za neparne.
Te sinuse i kosinuse stavljaju tu upravo zbog tih predznaka jer ide od -1 do +1 i u pravilu to im je jedina svrha.
Ajmo sad na zadatak.
Ak si dobro prepisao zadatak onda je niz trivijalan i ima samo jedan član {1}. Uvrsti pa ces vidjeti
Ak si krivo prepisao zadatak onda za parne n-ove niz je rastuc, i odozdo omeđen sa 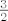 koji je ujedno i minimum jer se postiže a supremum je limes niza ilitiga koji je ujedno i minimum jer se postiže a supremum je limes niza ilitiga  i on se ne postize pa stoga nije max. i on se ne postize pa stoga nije max.
Za neparne n-ove, niz je padajuc i odozgo omeđen sa  koji je ujedno i max. Infimum je limes ilitiga koji je ujedno i max. Infimum je limes ilitiga  i on nije min jer se ne postiže. i on nije min jer se ne postiže.
inf = min{ , , 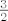 } = } = 
sup = max{ , ,  } }
Uoci da se ne postize ni inf niti sup pa nema niti min niti max.
To bi bilo to, nadam se da nisam napravio pacersku pogrešku... |
EDIT: evo pacerske pogreske, bum je ispravio...
EDIT2: pacerska pogreska je bila kaj nisam procitao cijeli thread i sad pretpostavljam da si ipak dobro napisao zadatak.
Prica i objasnjenja su ista kao i prije ovog edita al samo sa drugim brojkama.
Za neparne n-ove niz je trivijalnog oblika {1} dakle sup=max=inf=min=
za parne n-ove niz je odozdo omeđen sa  a odozgo sa a odozgo sa  i oni se ne postizu. i oni se ne postizu.
Dakle inf niza je 0 a supremum 2 i oni se ne postižu.
Valjda sam ovaj put dobro rijesio 
_________________
Though your dreams be tossed and blown...
|
|
| [Vrh] |
|
ivicasb1
Forumaš(ica)

Pridružen/a: 17. 04. 2009. (16:56:50)
Postovi: (5D)16
|
|
| [Vrh] |
|
Swerz
Forumaš(ica)


Pridružen/a: 13. 02. 2009. (21:30:28)
Postovi: (182)16
Spol: 
|
|
| [Vrh] |
|
ivicasb1
Forumaš(ica)

Pridružen/a: 17. 04. 2009. (16:56:50)
Postovi: (5D)16
|
|
| [Vrh] |
|
ivicasb1
Forumaš(ica)

Pridružen/a: 17. 04. 2009. (16:56:50)
Postovi: (5D)16
|
|
| [Vrh] |
|
Swerz
Forumaš(ica)


Pridružen/a: 13. 02. 2009. (21:30:28)
Postovi: (182)16
Spol: 
|
|
| [Vrh] |
|
Cobs
Forumaš(ica)


Pridružen/a: 21. 01. 2008. (13:32:15)
Postovi: (206)16
Spol: 
Lokacija: Geto
|
|
| [Vrh] |
|
ivicasb1
Forumaš(ica)

Pridružen/a: 17. 04. 2009. (16:56:50)
Postovi: (5D)16
|
|
| [Vrh] |
|
Swerz
Forumaš(ica)


Pridružen/a: 13. 02. 2009. (21:30:28)
Postovi: (182)16
Spol: 
|
|
| [Vrh] |
|
ivicasb1
Forumaš(ica)

Pridružen/a: 17. 04. 2009. (16:56:50)
Postovi: (5D)16
|
|
| [Vrh] |
|
Cobs
Forumaš(ica)


Pridružen/a: 21. 01. 2008. (13:32:15)
Postovi: (206)16
Spol: 
Lokacija: Geto
|
|
| [Vrh] |
|
ivicasb1
Forumaš(ica)

Pridružen/a: 17. 04. 2009. (16:56:50)
Postovi: (5D)16
|
|
| [Vrh] |
|
Cobs
Forumaš(ica)


Pridružen/a: 21. 01. 2008. (13:32:15)
Postovi: (206)16
Spol: 
Lokacija: Geto
|
|
| [Vrh] |
|
ivicasb1
Forumaš(ica)

Pridružen/a: 17. 04. 2009. (16:56:50)
Postovi: (5D)16
|
 Postano: 13:32 pet, 26. 2. 2010 Naslov: Postano: 13:32 pet, 26. 2. 2010 Naslov: |
    |
|
|
Hvala na odgovoru, ali ja ti nazalost ne kuzim na taj nacin koji si ti rijesio zadatak, nazalost :x
Ja sam cijelo vrijeme vjezbo na malo drukciji nacin.
Ja ti ima rijesen taj zadatak u primjeru jednog testa, ali ne kuzim samo 3.korak u njemu, pa ako ga ti kuzis ( na ovaj "moj nacin " ) pa da mi objasnis bili bi super :o
Ovako2.Korak [latex]bn = 4lim ( nprelaziubeskonacno) * \frac{(-1/4)^n -1} {-5/4}
= 3.korak 4*\frac{4}{5}= \frac{16}{5}
[/latex]
-ne kuzim ovaj treci korak,kako se iz 2. dobije treci.
Hvala
p.s napati me ovaj latex :D
Hvala na odgovoru, ali ja ti nazalost ne kuzim na taj nacin koji si ti rijesio zadatak, nazalost 
Ja sam cijelo vrijeme vjezbo na malo drukciji nacin.
Ja ti ima rijesen taj zadatak u primjeru jednog testa, ali ne kuzim samo 3.korak u njemu, pa ako ga ti kuzis ( na ovaj "moj nacin " ) pa da mi objasnis bili bi super 
Ovako2.Korak 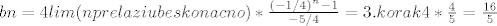
-ne kuzim ovaj treci korak,kako se iz 2. dobije treci.
Hvala
p.s napati me ovaj latex 
|
|
| [Vrh] |
|
Cobs
Forumaš(ica)


Pridružen/a: 21. 01. 2008. (13:32:15)
Postovi: (206)16
Spol: 
Lokacija: Geto
|
 Postano: 14:14 pet, 26. 2. 2010 Naslov: Postano: 14:14 pet, 26. 2. 2010 Naslov: |
    |
|
|
[quote="ivicasb1"]Hvala na odgovoru, ali ja ti nazalost ne kuzim na taj nacin koji si ti rijesio zadatak, nazalost :x
Ja sam cijelo vrijeme vjezbo na malo drukciji nacin.
Ja ti ima rijesen taj zadatak u primjeru jednog testa, ali ne kuzim samo 3. korak u njemu, pa ako ga ti kuzis ( na ovaj "moj nacin " ) pa da mi objasnis bili bi super :o
Ovako1.Korak [latex]bn = 4* \frac{1^n -1}{4}{5}{-4}
2.korak 4 \displaystyle\lim_{n \to \infty} \frac{1}{4}^n -1 {-5}{4}
3.korak 4*\frac{4}{5}= \frac{16}{5}
[/latex]
E ja ne kuzim ovaj drugi korak,kako se iz njega dobije 3 korak ( 4*\frac{4}{5} )[/quote]
ja ti ovo niš nemrem skužit kaj si napiso... pa ti svakako preporučam:
1.skini ovo: [url=http://miktex.org/2.8/setup]miktex[/url] ( to ti je free programcic za pisanje latex - a )
2. prouči ovo: [url=http://web.math.hr/~ungar/lkratko2e_internet.pdf]latex[/url]
3. ne moraš samo to, imaš po internetu materijala za latex ko pljeve ( sam upisi latex tutorial u google ).
Ja sam naučio pisati pomoću latex-a za par dana ( ono osnovno, ne samo matematicke formule )
4. primi se posla i nauci nešto korisno ( a i olakšat ćeš ljudima posao dešifriranja postova )
Inače s obzirom da nisam uspio skužit tvoj post probat ću ti objasnit svoj:
objasnit cu ti od ove rečenice( pretpostavljam da ovo prije znaš ):
[quote="Ja"]pa vec sam napisao to je: [/quote]
pa u startu imaš limes po [latex]n[/latex] koji teži u [latex]+\infty[/latex] od sume koja ide po [latex]k[/latex] do [latex]n[/latex]( k ide od 1 ). To je isto ko i da pise suma po [latex]k[/latex] do [latex]+\infty[/latex] ( u ovom slucaju bez limesa ispred )( k opet ide od 1 ). Naravno sad kad sam se "rješio" limesa imam sumu nečega( [latex]b_k[/latex] ) po nekom indeksu ( svejedno mi je dal pisem da mi suma ide po k ili po n, pa sam stavio n ). Sad kad sam se rješio limesa idem si malo pojednostaviti izraz po kojemu sumiram, pa ću izlučiti 4, iz izraza[latex](-1)^n-1\cdot4^{-n+2}[/latex], tu četvorku ću stavit ispred sume i ono po čemu sada sumiram je: [latex](-1)^{n-1}\cdot4^{-n+1}[/latex]. ( Primjeti ponovno da n ide od 1 ). Pogledaj sad izraz:
[latex](-1)^n-1\cdot4^{-n+1}[/latex] , za [latex] n = 1 [/latex] to je jednako: [latex](-1)^0\cdot4^0[/latex]
za [latex]n = 2[/latex] izraz je jednak: [latex](-1)^1\cdot4^{-1} = -\frac{1}{4}[/latex] ... možeš za par sljedećih sam.
Kad malo raspišeš tu sumu vidiš da ti je ista ko i da si krenuo od 0 sa članom sumacije: [latex](-1)^n\cdot4^{-n} = \left(-\frac{1}{4}\right)^n[/latex] ( to se lagano da dobiti sa supstituciom npr: t = n - 1 ).
Sad ono što si dobio je geometrijski red gdje je [latex]q \in <-1,1>[/latex] ( q = -1/4 ) tj, taj red konvergira, ak neznas formulu za konvergenciju geom. reda, uzmi formulu za konvergenciju geom. niza ( prvih n - članova ) i baci na to limes kada n ide u beskonacno
| ivicasb1 (napisa): | Hvala na odgovoru, ali ja ti nazalost ne kuzim na taj nacin koji si ti rijesio zadatak, nazalost 
Ja sam cijelo vrijeme vjezbo na malo drukciji nacin.
Ja ti ima rijesen taj zadatak u primjeru jednog testa, ali ne kuzim samo 3. korak u njemu, pa ako ga ti kuzis ( na ovaj "moj nacin " ) pa da mi objasnis bili bi super 
Ovako1.Korak 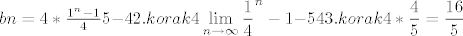
E ja ne kuzim ovaj drugi korak,kako se iz njega dobije 3 korak ( 4*\frac{4}{5} ) |
ja ti ovo niš nemrem skužit kaj si napiso... pa ti svakako preporučam:
1.skini ovo: miktex ( to ti je free programcic za pisanje latex - a )
2. prouči ovo: latex
3. ne moraš samo to, imaš po internetu materijala za latex ko pljeve ( sam upisi latex tutorial u google ).
Ja sam naučio pisati pomoću latex-a za par dana ( ono osnovno, ne samo matematicke formule )
4. primi se posla i nauci nešto korisno ( a i olakšat ćeš ljudima posao dešifriranja postova )
Inače s obzirom da nisam uspio skužit tvoj post probat ću ti objasnit svoj:
objasnit cu ti od ove rečenice( pretpostavljam da ovo prije znaš ):
| Ja (napisa): | | pa vec sam napisao to je: |
pa u startu imaš limes po  koji teži u koji teži u  od sume koja ide po od sume koja ide po  do do  ( k ide od 1 ). To je isto ko i da pise suma po ( k ide od 1 ). To je isto ko i da pise suma po  do do  ( u ovom slucaju bez limesa ispred )( k opet ide od 1 ). Naravno sad kad sam se "rješio" limesa imam sumu nečega( ( u ovom slucaju bez limesa ispred )( k opet ide od 1 ). Naravno sad kad sam se "rješio" limesa imam sumu nečega( 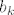 ) po nekom indeksu ( svejedno mi je dal pisem da mi suma ide po k ili po n, pa sam stavio n ). Sad kad sam se rješio limesa idem si malo pojednostaviti izraz po kojemu sumiram, pa ću izlučiti 4, iz izraza ) po nekom indeksu ( svejedno mi je dal pisem da mi suma ide po k ili po n, pa sam stavio n ). Sad kad sam se rješio limesa idem si malo pojednostaviti izraz po kojemu sumiram, pa ću izlučiti 4, iz izraza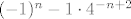 , tu četvorku ću stavit ispred sume i ono po čemu sada sumiram je: , tu četvorku ću stavit ispred sume i ono po čemu sada sumiram je: 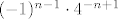 . ( Primjeti ponovno da n ide od 1 ). Pogledaj sad izraz: . ( Primjeti ponovno da n ide od 1 ). Pogledaj sad izraz:
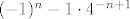 , za , za 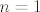 to je jednako: to je jednako: 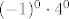
za  izraz je jednak: izraz je jednak: 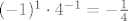 ... možeš za par sljedećih sam. ... možeš za par sljedećih sam.
Kad malo raspišeš tu sumu vidiš da ti je ista ko i da si krenuo od 0 sa članom sumacije: 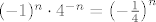 ( to se lagano da dobiti sa supstituciom npr: t = n - 1 ). ( to se lagano da dobiti sa supstituciom npr: t = n - 1 ).
Sad ono što si dobio je geometrijski red gdje je 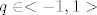 ( q = -1/4 ) tj, taj red konvergira, ak neznas formulu za konvergenciju geom. reda, uzmi formulu za konvergenciju geom. niza ( prvih n - članova ) i baci na to limes kada n ide u beskonacno ( q = -1/4 ) tj, taj red konvergira, ak neznas formulu za konvergenciju geom. reda, uzmi formulu za konvergenciju geom. niza ( prvih n - članova ) i baci na to limes kada n ide u beskonacno
|
|
| [Vrh] |
|
ivicasb1
Forumaš(ica)

Pridružen/a: 17. 04. 2009. (16:56:50)
Postovi: (5D)16
|
 Postano: 17:00 pet, 26. 2. 2010 Naslov: Postano: 17:00 pet, 26. 2. 2010 Naslov: |
    |
|
|
E ovako ide cijeli zadatak sa rjesenjem ( nadam se da ces sad bolje skuzit , malo sam se vise potrudio :shock: )
[latex]1.korak: b_n = 4-1+\frac {1}{4} - \frac{1}{16}+......+\frac{(-1)^n-1 ( jedan ide gore sa n)} {4^n-2 (2 ide gore sa n)}[/latex]
[latex]2.korak:b_n = 4* \frac{(-1/4)^n -1}{-1/4 -1}[/latex]
[latex]3.korak:4 \displaystyle\lim_{n \to \infty}\frac{(-1/4)^n -1}{-5/4} [/latex][latex]=4*4/5 = 16/5[/latex]
E sad , nije mi jasno kako se u iz 2. koraka izvede 3.korak tj. kako smo dobili 3. korak, ako mozes pojasniti ( jer ovaj tvoj nacin,nazalost ne kuzim ipak hvala na trudu! )
zivcira me zato sto znam da je neka vrlo mala greskica tj. nacin na koji se dobije na kraju 4* 4/5 = 16/5 a ja je ne mogu trenutno otkriti :evil:
E ovako ide cijeli zadatak sa rjesenjem ( nadam se da ces sad bolje skuzit , malo sam se vise potrudio  ) )
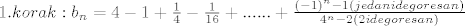
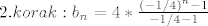
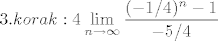 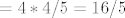
E sad , nije mi jasno kako se u iz 2. koraka izvede 3.korak tj. kako smo dobili 3. korak, ako mozes pojasniti ( jer ovaj tvoj nacin,nazalost ne kuzim ipak hvala na trudu! )
zivcira me zato sto znam da je neka vrlo mala greskica tj. nacin na koji se dobije na kraju 4* 4/5 = 16/5 a ja je ne mogu trenutno otkriti 
Zadnja promjena: ivicasb1; 17:40 pet, 26. 2. 2010; ukupno mijenjano 1 put.
|
|
| [Vrh] |
|
Swerz
Forumaš(ica)


Pridružen/a: 13. 02. 2009. (21:30:28)
Postovi: (182)16
Spol: 
|
|
| [Vrh] |
|
ivicasb1
Forumaš(ica)

Pridružen/a: 17. 04. 2009. (16:56:50)
Postovi: (5D)16
|
|
| [Vrh] |
|
|













