| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
pbakic
Forumaš(ica)

Pridružen/a: 05. 10. 2009. (17:48:30)
Postovi: (143)16
Spol: 
|
|
| [Vrh] |
|
some_dude
Forumaš(ica)
Pridružen/a: 08. 11. 2009. (16:23:13)
Postovi: (59)16
Spol: 
Lokacija: Zd-Zg
|
|
| [Vrh] |
|
meda
Forumaš(ica)

Pridružen/a: 09. 01. 2010. (09:29:23)
Postovi: (A0)16
|
|
| [Vrh] |
|
Genaro
Forumaš(ica)

Pridružen/a: 27. 10. 2009. (18:57:50)
Postovi: (8B)16
Spol: 
Lokacija: Zagreb
|
|
| [Vrh] |
|
meda
Forumaš(ica)

Pridružen/a: 09. 01. 2010. (09:29:23)
Postovi: (A0)16
|
|
| [Vrh] |
|
Genaro
Forumaš(ica)

Pridružen/a: 27. 10. 2009. (18:57:50)
Postovi: (8B)16
Spol: 
Lokacija: Zagreb
|
|
| [Vrh] |
|
meda
Forumaš(ica)

Pridružen/a: 09. 01. 2010. (09:29:23)
Postovi: (A0)16
|
|
| [Vrh] |
|
pmli
Forumaš(ica)

Pridružen/a: 09. 11. 2009. (12:03:05)
Postovi: (2C8)16
Spol: 
|
|
| [Vrh] |
|
meda
Forumaš(ica)

Pridružen/a: 09. 01. 2010. (09:29:23)
Postovi: (A0)16
|
|
| [Vrh] |
|
smajl
Forumaš(ica)

Pridružen/a: 02. 01. 2010. (12:59:23)
Postovi: (EB)16
Spol: 
Lokacija: Zagreb
|
|
| [Vrh] |
|
pbakic
Forumaš(ica)

Pridružen/a: 05. 10. 2009. (17:48:30)
Postovi: (143)16
Spol: 
|
|
| [Vrh] |
|
smajl
Forumaš(ica)

Pridružen/a: 02. 01. 2010. (12:59:23)
Postovi: (EB)16
Spol: 
Lokacija: Zagreb
|
|
| [Vrh] |
|
pbakic
Forumaš(ica)

Pridružen/a: 05. 10. 2009. (17:48:30)
Postovi: (143)16
Spol: 
|
|
| [Vrh] |
|
meda
Forumaš(ica)

Pridružen/a: 09. 01. 2010. (09:29:23)
Postovi: (A0)16
|
|
| [Vrh] |
|
mornik
Forumaš(ica)

Pridružen/a: 26. 09. 2009. (06:25:44)
Postovi: (128)16
|
 Postano: 17:47 pon, 12. 4. 2010 Naslov: Postano: 17:47 pon, 12. 4. 2010 Naslov: |
    |
|
|
Dobro, dakle, funkcija je očito diferencijabilna svugdje osim u [latex]\displaystyle\frac{\pi}{4}[/latex]. Ne znam koliko ti je to očito, ali stvar je zapravo dosta primitivna - ukoliko [latex]\arctan x\neq 1[/latex], onda zbog neprekidnosti arkus tangensa (ovo se da i puno preciznije raspisati, dakako :)) postoji neka okolina oko [latex]x[/latex] takva da za svaki [latex]t[/latex] iz te okoline vrijedi [latex]\arctan t\neq 1[/latex]. U tom slučaju, na cijeloj toj okolini možeš "maknuti" apsolutnu vrijednost (dakle, zamijeniti ju s time što piše unutar apsolutne vrijednosti ili s tim pomnoženim s [latex]-1[/latex]), a onda imaš "običnu" diferencijabilnu funkciju.
Ne znam koliko ti je ovo bilo jasno, ali stvar je samo u tome da nam je jedina "sumnjiva točka" tamo gdje se apsolutna vrijednost "prelama", tj. tamo gdje je arkus tangens upravo jednak [latex]1[/latex]. Dobro, sad smo se riješili svih točaka osim [latex]\displaystyle\frac{\pi}{4}[/latex]. Za to je naprosto najbolje, rekao bih, ići po definiciji - dakle, pogledati je li limes slijeva onog razlomka kojim je derivacija definirana jednak limesu zdesna. I to je to, ako nisam pogriješio. :)
Dobro, dakle, funkcija je očito diferencijabilna svugdje osim u  . Ne znam koliko ti je to očito, ali stvar je zapravo dosta primitivna - ukoliko . Ne znam koliko ti je to očito, ali stvar je zapravo dosta primitivna - ukoliko 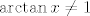 , onda zbog neprekidnosti arkus tangensa (ovo se da i puno preciznije raspisati, dakako , onda zbog neprekidnosti arkus tangensa (ovo se da i puno preciznije raspisati, dakako  ) postoji neka okolina oko ) postoji neka okolina oko  takva da za svaki takva da za svaki  iz te okoline vrijedi iz te okoline vrijedi 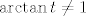 . U tom slučaju, na cijeloj toj okolini možeš "maknuti" apsolutnu vrijednost (dakle, zamijeniti ju s time što piše unutar apsolutne vrijednosti ili s tim pomnoženim s . U tom slučaju, na cijeloj toj okolini možeš "maknuti" apsolutnu vrijednost (dakle, zamijeniti ju s time što piše unutar apsolutne vrijednosti ili s tim pomnoženim s  ), a onda imaš "običnu" diferencijabilnu funkciju. ), a onda imaš "običnu" diferencijabilnu funkciju.
Ne znam koliko ti je ovo bilo jasno, ali stvar je samo u tome da nam je jedina "sumnjiva točka" tamo gdje se apsolutna vrijednost "prelama", tj. tamo gdje je arkus tangens upravo jednak  . Dobro, sad smo se riješili svih točaka osim . Dobro, sad smo se riješili svih točaka osim  . Za to je naprosto najbolje, rekao bih, ići po definiciji - dakle, pogledati je li limes slijeva onog razlomka kojim je derivacija definirana jednak limesu zdesna. I to je to, ako nisam pogriješio. . Za to je naprosto najbolje, rekao bih, ići po definiciji - dakle, pogledati je li limes slijeva onog razlomka kojim je derivacija definirana jednak limesu zdesna. I to je to, ako nisam pogriješio. 
|
|
| [Vrh] |
|
meda
Forumaš(ica)

Pridružen/a: 09. 01. 2010. (09:29:23)
Postovi: (A0)16
|
|
| [Vrh] |
|
A_je_to
Forumaš(ica)

Pridružen/a: 19. 02. 2009. (16:51:22)
Postovi: (6D)16
Spol: 
|
|
| [Vrh] |
|
genchy
Forumaš(ica)

Pridružen/a: 03. 09. 2009. (18:32:56)
Postovi: (29)16
|
|
| [Vrh] |
|
|














