Redovi

[A_je_to]

Zamolio bi nekog da mi objasni kako u gornjem izrazu "ubaciti" u sumu. Hvala!

[c.p.-23]

kako razviti f(x)=x^(-1)cos(x) u Taylorov red oko točke 1 ...?

[pmli]

@A_je_to: Nema potrebe za "ubacivanjem" u sumu, ali je zgodno da se vidi koji je broj uz koju potenciju. Pritom mislim na x^0 (on se pojavljuje izvan i unutar sume). Stoga se to sve može zapisati ovako:

@c.p.-23: Supstitucija y=x-1, adicijska formula za cos, produkti redova. Najjednostavnije što sam uspio dobiti je

[niveus]

Razviti funkciju f(x)= arcsinx/sqrt(1-x^2) oko točke c=0


Hvala

[pmli]

Produkt redova. Dobi se

[marichuy]

3.33. pod a) http://web.math.hr/nastava/analiza/files/ch3_3.pdf
Hvala!

[pmli]

Rastav na parcijalne razlomke. Zatim se sjetiti Maclaurinovog reda od ln(1+x).

[pbakic]

lol, opet kasnim... sry

Recimo, krenemo od funkcije 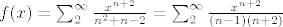, pa cemo gledati njezinu vrijednost u -1 kad je nadjemo. (Ovih n+2 smo stavili nad x jer je 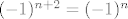, a n+2 je bolje jer cemo derivirati.)

Sad to deriviramo, dobijemo .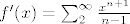
Sad se zelimo rijesiti i ovog n-1, pa podijelimo sve sa x^2 i deriviramo ⇒


.
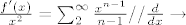
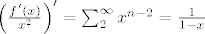Sad samo odvrtimo film unazad da bismo dobili f(x), dakle desnu stranu integriramo (dobijemo -ln(1-x)) pa mnozimo s x^2 pa opet integriramo (parcijalna). Nakon toga smo dobili f(x) pa samo uvrstimo -1 i dobijemo sumu

[niveus]

@pmli hvala

Razviti funkciju f(x)=sin^4(x)+cos^4(x) c=1

[andra]

moze jedno pitanje... kod racunanja taylerovih redova, ja lijepo zadatak rastavim na dva reda, izracunam svaki posebno i onda zapnem jer neznam kako da ih izmnozim??

[pmli]

[marichuy]

pbakic tako sam i ja radila,al' nisam imala volje ovo "vraćat" , pa sam misla da ima neko efikasnije rješenje....
Hvala!

[andra]

moze pomoc oko zadatka 3.31 po c)
ln(x^2 +x-6), c=2

kada zamjenim sa y=x-2 i to sve malo raspisem dobijem lny+ln5+ln(1+(y/5)) i sad neznam kaj bi sa lny??

[pmli]

O tome se već raspravljalo. Taj član ostavi na miru, jer da bi nešto moglo imati Taylorov red, treba biti klase , a ln ne da nije u toj klasi oko 0, nego nije ni definiran u 0.

[kikyca]

kako da razvijem (x/(x^2+1))^3??

[pmli]

, binomna formula

[kikyca]

[pbakic]

Pa x^3 je klase , kao i svaki polinom, samo sto je vecina derivacija te funkcije jednaka 0. Ali u ovom slucaju to opce ne igra, samo se kasnije red pomnozi s x^3

[NeonBlack]

Samo da se mao konzultiram , ovo izračunavanje suma( koje je bar grupa od M-R radila zadnji sat), ne znam riješit neke primjere u "Zadatcima za vježbu", a vidim da se ti svode na uporabu Abeovog tm., sad ne znam trebam i to proć sama jer to mogu očekivat na kolokviju ili ne? A s druge strane asistent Mimica je rekao da dosta stvari što je u toj skripti ne ćemo raditi i na zadnjem satu je rekao da gotovo sigurno možemo očekivati ono izarčunavanje suma u kojima su razomci pa se riješava po prepoznavanju uzorka.
Eto, zanima me šta ćete vi ( za kolokvij)?

[kaj]