| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
crazyivan
Gost
|
|
| [Vrh] |
|
vsego
Site Admin
Pridružen/a: 06. 10. 2002. (22:07:09)
Postovi: (3560)16
Spol: 
Lokacija: /sbin/init
|
 Postano: 20:27 sub, 4. 7. 2009 Naslov: |
    |
|
|
Da jednom ispadnu razliciti brojevi, vjerojatnost je 5/6 (na prvoj kocki padne bilo sto; na drugoj bilo sto osim 5 preostalih brojeva). :) Da sva tri puta budu oba broja razlicita, vjerojatnost je [latex](5/6)^3[/latex]. :)
Dakle, da se barem jednom pojave dva ista broja, vjerojatnost je
[latex]1-\left(\frac{5}{6}\right)^3 = \frac{91}{216}[/latex],
sto se ne pojavljuje u tvojim odgovorima. :?
No, ako te zanima da se [b]tocno[/b] jednom pojave isti brojevi, onda je to:
[latex]3\cdot\frac{1}{6}\cdot\frac{5}{6}\cdot\frac{5}{6} = \frac{75}{216}[/latex]. 8)
Da jednom ispadnu razliciti brojevi, vjerojatnost je 5/6 (na prvoj kocki padne bilo sto; na drugoj bilo sto osim 5 preostalih brojeva).  Da sva tri puta budu oba broja razlicita, vjerojatnost je  .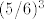
Dakle, da se barem jednom pojave dva ista broja, vjerojatnost je
 ,
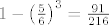sto se ne pojavljuje u tvojim odgovorima. 
No, ako te zanima da se tocno jednom pojave isti brojevi, onda je to:
 . 
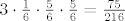_________________ U pravilu ignoriram pitanja u krivim topicima i kodove koji nisu u [code]...[/code] blokovima.
Takodjer, OBJASNITE sto vas muci! "Sto mi je krivo?", bez opisa u cemu je problem, rijetko ce zadobiti moju paznju.  |
|
| [Vrh] |
|
Ywannah
Gost
|
| Postano: 15:42 ned, 5. 7. 2009 Naslov: |
|
|
|
I ja se mučim sa sličnim zadacima. Nažalost, nisam shvatila ni ovaj koji je ovdje riješen. :oops: Ali, eto, ako mi netko može ove riješiti, bila bih jaaako zahvalna. :D
1.U ravnini se nalazi pet kružnica. Koliko maksimalno ima sjecišta?
(25, 20, 10, 16)
3. Kolika je vjerojatnost da u dva bacanja kocke padne broj čiji je zbroj 5?
4. Koliko najmanje znamenki oktalnog brojevnog sustava ( sustava s bazom 8 ) nam je potrebno da bismo mogli zapisati bilo koji broj koji se može zapisati u 4 znamenke dekadskog sustava?
(7, 5, 6, 8)
5. Koliko najmanje znamenki ternarnog sustava nam je potrebno da bi mogli zapisati bilo koji broj koji se može zapisati u 4 znamenke dekadskog sustava?
6. Bacamo novčić tri puta, i sva tri puta dobijemo pismo. Vjerojatnost da ćemo i četvrti put dobiti pismo je? (25%, 6.25%, 12.5%, 50%)
14. Na koliko najviše područja mogu tri kružnice podijeliti ravninu??
(11, 27, 8, 4)
I ja se mučim sa sličnim zadacima. Nažalost, nisam shvatila ni ovaj koji je ovdje riješen.  Ali, eto, ako mi netko može ove riješiti, bila bih jaaako zahvalna. 
1.U ravnini se nalazi pet kružnica. Koliko maksimalno ima sjecišta?
(25, 20, 10, 16)
3. Kolika je vjerojatnost da u dva bacanja kocke padne broj čiji je zbroj 5?
4. Koliko najmanje znamenki oktalnog brojevnog sustava ( sustava s bazom 8 ) nam je potrebno da bismo mogli zapisati bilo koji broj koji se može zapisati u 4 znamenke dekadskog sustava?
(7, 5, 6,
5. Koliko najmanje znamenki ternarnog sustava nam je potrebno da bi mogli zapisati bilo koji broj koji se može zapisati u 4 znamenke dekadskog sustava?
6. Bacamo novčić tri puta, i sva tri puta dobijemo pismo. Vjerojatnost da ćemo i četvrti put dobiti pismo je? (25%, 6.25%, 12.5%, 50%)
14. Na koliko najviše područja mogu tri kružnice podijeliti ravninu??
(11, 27, 8, 4)
|
|
| [Vrh] |
|
ma
Forumaš(ica)
Pridružen/a: 27. 01. 2007. (12:06:50)
Postovi: (347)16
Spol: 
|
| Postano: 16:23 ned, 5. 7. 2009 Naslov: |
|
|
|
[quote="Ywannah"]1.U ravnini se nalazi pet kružnica. Koliko maksimalno ima sjecišta?
(25, 20, 10, 16)[/quote]
(ako pretpostavimo da su sve kružnice različite :D ) maksimalni broj sjecišta dvije kružnice je 2, a može se napraviti da nijedna dva sjecišta nisu u istoj točki. znači svaka kružnica siječe ostale 4 u 2 točke svaku, što iznosi [latex]5\cdot 8 = 40[/latex], no svako sjecište smo brojali iz perspektive obje kružnice kojima pripada pa to još dijelimo s 2, što daje rješenje: [latex]20[/latex].
[size=9][color=#999999]Added after 5 minutes:[/color][/size]
[quote="Ywannah"]3. Kolika je vjerojatnost da u dva bacanja kocke padne broj čiji je zbroj 5?[/quote]
sastavljač zadatka se malo muči s jezikom :PP (u 2 bacanja kocke će pasti 2 broja)
ono što ti odgovara su sljedeći slučajevi:
(broj na 1. kocki, broj na 2. kocki) smije biti:
(1,4)
(2,3)
(3,2)
(4,1)
dakle, 4 od mogućih 36 ishoda. vjerojatnost je [latex]\frac{4}{36}=\frac{1}{9}[/latex].
[size=9][color=#999999]Added after 3 minutes:[/color][/size]
[quote="Ywannah"]4. Koliko najmanje znamenki oktalnog brojevnog sustava ( sustava s bazom 8 ) nam je potrebno da bismo mogli zapisati bilo koji broj koji se može zapisati u 4 znamenke dekadskog sustava?
(7, 5, 6, 8)[/quote]
pitanje mi nije baš najjasnije... pa sigurno nam treba svih 8 znamenki oktalnog sustava da bismo zapisali [b]bilokoji[/b] četveroznamenkasti broj dekadskog sustava... :?
[size=9][color=#999999]Added after 1 minutes:[/color][/size]
[quote="Ywannah"]5. Koliko najmanje znamenki ternarnog sustava nam je potrebno da bi mogli zapisati bilo koji broj koji se može zapisati u 4 znamenke dekadskog sustava? [/quote]
pozvao bih se na ovo gore i rekao: 3.
[size=9][color=#999999]Added after 2 minutes:[/color][/size]
[quote="Ywannah"]6. Bacamo novčić tri puta, i sva tri puta dobijemo pismo. Vjerojatnost da ćemo i četvrti put dobiti pismo je? (25%, 6.25%, 12.5%, 50%)[/quote]
uuuuu... trik pitanje :sillyroll: da je ponuđeno 100% još bi se čovjek i zamislio o ispravnosti novčića, ali ovako je sigurno 50%. za svako bacanje je 50:50.
[size=9][color=#999999]Added after 3 minutes:[/color][/size]
[quote="Ywannah"]14. Na koliko najviše područja mogu tri kružnice podijeliti ravninu??
(11, 27, 8, 4)[/quote]
da je više kružnica ovo bi bilo teže pitanje, ali za samo tri kružnice možeš si i nacrtati sliku i vidjeti da ne možeš dobiti više od 8 područja.
| Ywannah (napisa): | 1.U ravnini se nalazi pet kružnica. Koliko maksimalno ima sjecišta?
(25, 20, 10, 16) |
(ako pretpostavimo da su sve kružnice različite ) maksimalni broj sjecišta dvije kružnice je 2, a može se napraviti da nijedna dva sjecišta nisu u istoj točki. znači svaka kružnica siječe ostale 4 u 2 točke svaku, što iznosi 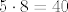 , no svako sjecište smo brojali iz perspektive obje kružnice kojima pripada pa to još dijelimo s 2, što daje rješenje:  .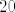
Added after 5 minutes:
| Ywannah (napisa): | | 3. Kolika je vjerojatnost da u dva bacanja kocke padne broj čiji je zbroj 5? |
sastavljač zadatka se malo muči s jezikom  (u 2 bacanja kocke će pasti 2 broja)
ono što ti odgovara su sljedeći slučajevi:
(broj na 1. kocki, broj na 2. kocki) smije biti:
(1,4)
(2,3)
(3,2)
(4,1)
dakle, 4 od mogućih 36 ishoda. vjerojatnost je  .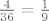
Added after 3 minutes:
| Ywannah (napisa): | 4. Koliko najmanje znamenki oktalnog brojevnog sustava ( sustava s bazom 8 ) nam je potrebno da bismo mogli zapisati bilo koji broj koji se može zapisati u 4 znamenke dekadskog sustava?
(7, 5, 6, |
pitanje mi nije baš najjasnije... pa sigurno nam treba svih 8 znamenki oktalnog sustava da bismo zapisali bilokoji četveroznamenkasti broj dekadskog sustava...
Added after 1 minutes:
| Ywannah (napisa): | | 5. Koliko najmanje znamenki ternarnog sustava nam je potrebno da bi mogli zapisati bilo koji broj koji se može zapisati u 4 znamenke dekadskog sustava? |
pozvao bih se na ovo gore i rekao: 3.
Added after 2 minutes:
| Ywannah (napisa): | | 6. Bacamo novčić tri puta, i sva tri puta dobijemo pismo. Vjerojatnost da ćemo i četvrti put dobiti pismo je? (25%, 6.25%, 12.5%, 50%) |
uuuuu... trik pitanje  da je ponuđeno 100% još bi se čovjek i zamislio o ispravnosti novčića, ali ovako je sigurno 50%. za svako bacanje je 50:50.
Added after 3 minutes:
| Ywannah (napisa): | 14. Na koliko najviše područja mogu tri kružnice podijeliti ravninu??
(11, 27, 8, 4) |
da je više kružnica ovo bi bilo teže pitanje, ali za samo tri kružnice možeš si i nacrtati sliku i vidjeti da ne možeš dobiti više od 8 područja.
_________________
ima let u finish
|
|
| [Vrh] |
|
rafaelm
Forumaš(ica)
Pridružen/a: 24. 12. 2006. (13:30:11)
Postovi: (21F)16
Spol:
Lokacija: Zagreb
|
|
| [Vrh] |
|
crazyivan
Gost
|
|
| [Vrh] |
|
crazyivan
Gost
|
|
| [Vrh] |
|
stuey
Forumaš(ica)
Pridružen/a: 03. 11. 2006. (15:52:11)
Postovi: (A2)16
Spol:
Lokacija: Rijeka, Zg
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
KikePike
Gost
|
|
| [Vrh] |
|
Gost
|
| Postano: 14:22 uto, 28. 7. 2009 Naslov: |
|
|
|
[quote="KikePike"]Evo, imam jedno slično pitanje skroz, ali nisam sigurna da sam točno riješila.
Bacamo kocku s brojevima od 1 do 6. Kolika je vjerojatnost da se u tri bacanja pojave točno dvije šestice?
3 * 1/6 * 1/6 * 5/6 = 15/216 ?
Ili ide bez 3* ? Ne znaaam. :shock:[/quote]
Ja bih rekao bez 3, ali nisam siguran.
Zato jer: Ako bacamo kockicu prvi put, sansa da dobijemo sesticu je 1/6. Kad je bacimo ponovo, i recimo da opet zelimo sesticu, to nam je 1/36, da ce u ta 2 bacanja dva puta pasti sestica. A sada imamo treci pokusaj, gdje zelimo da nam padne sve osim sestice, tako da je tu sansa 5/6. Tako da bih ja rekao: (1/6)^2 * 5/6. Ispravite me ako grijesim.
| KikePike (napisa): | Evo, imam jedno slično pitanje skroz, ali nisam sigurna da sam točno riješila.
Bacamo kocku s brojevima od 1 do 6. Kolika je vjerojatnost da se u tri bacanja pojave točno dvije šestice?
3 * 1/6 * 1/6 * 5/6 = 15/216 ?
Ili ide bez 3* ? Ne znaaam.  |
Ja bih rekao bez 3, ali nisam siguran.
Zato jer: Ako bacamo kockicu prvi put, sansa da dobijemo sesticu je 1/6. Kad je bacimo ponovo, i recimo da opet zelimo sesticu, to nam je 1/36, da ce u ta 2 bacanja dva puta pasti sestica. A sada imamo treci pokusaj, gdje zelimo da nam padne sve osim sestice, tako da je tu sansa 5/6. Tako da bih ja rekao: (1/6)^2 * 5/6. Ispravite me ako grijesim.
|
|
| [Vrh] |
|
vsego
Site Admin
Pridružen/a: 06. 10. 2002. (22:07:09)
Postovi: (3560)16
Spol:
Lokacija: /sbin/init
|
| Postano: 17:05 uto, 28. 7. 2009 Naslov: |
|
|
|
Rezoniranje je dobro, ali primjenjivo na situaciju "kolika je vjerojatnost da u prva dva bacanja padne sestica, a u trecem ne". :) Ovdje nas zanima "u bilo koja dva bacanja padne sestica, a u preostalom ne". 8) Dakle:
- 66x
- 6x6
- x66
(za x = 1, 2, 3, 4 ili 5). Nadam se da je sada jasno. :)
Rezoniranje je dobro, ali primjenjivo na situaciju "kolika je vjerojatnost da u prva dva bacanja padne sestica, a u trecem ne". Ovdje nas zanima "u bilo koja dva bacanja padne sestica, a u preostalom ne". Dakle:
- 66x
- 6x6
- x66
(za x = 1, 2, 3, 4 ili 5). Nadam se da je sada jasno.
_________________ U pravilu ignoriram pitanja u krivim topicima i kodove koji nisu u [code]...[/code] blokovima.
Takodjer, OBJASNITE sto vas muci! "Sto mi je krivo?", bez opisa u cemu je problem, rijetko ce zadobiti moju paznju. |
|
| [Vrh] |
|
Fazh
Forumaš s poteškoćama u pisanju
Pridružen/a: 09. 11. 2008. (22:51:55)
Postovi: (D)16
Lokacija: Jucer
|
| Postano: 23:16 pon, 3. 8. 2009 Naslov: |
|
|
|
[quote="Anonymous"]
Ja bih rekao bez 3, ali nisam siguran.
Zato jer: Ako bacamo kockicu prvi put, sansa da dobijemo sesticu je 1/6. Kad je bacimo ponovo, i recimo da opet zelimo sesticu, to nam je 1/36, da ce u ta 2 bacanja dva puta pasti sestica. A sada imamo treci pokusaj, gdje zelimo da nam padne sve osim sestice, tako da je tu sansa 5/6. Tako da bih ja rekao: (1/6)^2 * 5/6. Ispravite me ako grijesim.[/quote]
Ovo gore sam ja napisao, ali nisam skuzio da sam log out-an. :)
Anyway, nisam sigran da pratim ovo sto si rekao vsego.
Ako razmisljam ovako: Svejedno mi je dali 1 kockicu bacim 3 puta, ili da uzmem 3 kockice i da bacim 1 put i zelim tocno 2 sestice da dodu.
Uzevsi to u obzir, ja imam (1/6)^2*5/6 sansu, i sad nemogu reci koja kockica mi je "prvo bacanje" ili prva kockica, tako da nevidim potrebu da tim da tocno odredim u kojem slucaju sestica Nije pala, niti je to moguce ako bacam 3 odjednom. Tako da zasad ipak ostajem pri svojem misljenju :D , ali molio bih objasnjenje u slucaju da sam pogrijesio/krivo shvatio/izracunao :) .
| Anonymous (napisa): |
Ja bih rekao bez 3, ali nisam siguran.
Zato jer: Ako bacamo kockicu prvi put, sansa da dobijemo sesticu je 1/6. Kad je bacimo ponovo, i recimo da opet zelimo sesticu, to nam je 1/36, da ce u ta 2 bacanja dva puta pasti sestica. A sada imamo treci pokusaj, gdje zelimo da nam padne sve osim sestice, tako da je tu sansa 5/6. Tako da bih ja rekao: (1/6)^2 * 5/6. Ispravite me ako grijesim. |
Ovo gore sam ja napisao, ali nisam skuzio da sam log out-an.
Anyway, nisam sigran da pratim ovo sto si rekao vsego.
Ako razmisljam ovako: Svejedno mi je dali 1 kockicu bacim 3 puta, ili da uzmem 3 kockice i da bacim 1 put i zelim tocno 2 sestice da dodu.
Uzevsi to u obzir, ja imam (1/6)^2*5/6 sansu, i sad nemogu reci koja kockica mi je "prvo bacanje" ili prva kockica, tako da nevidim potrebu da tim da tocno odredim u kojem slucaju sestica Nije pala, niti je to moguce ako bacam 3 odjednom. Tako da zasad ipak ostajem pri svojem misljenju , ali molio bih objasnjenje u slucaju da sam pogrijesio/krivo shvatio/izracunao .
|
|
| [Vrh] |
|
vsego
Site Admin
Pridružen/a: 06. 10. 2002. (22:07:09)
Postovi: (3560)16
Spol:
Lokacija: /sbin/init
|
| Postano: 12:51 uto, 4. 8. 2009 Naslov: |
|
|
|
Ali ti racunas ukupni broj mogucnosti kao [latex]6^3[/latex], sto znaci da razlikujes kocke (bilo kao prvu, drugu i trecu, bilo kao prvo, drugo i trece bacanje iste kocke). :) Dakle, tebi je [tt]abc[/tt] razlicito bacanje od [tt]bca[/tt], pa moras razlikovati kocke. :tso:
Ajmo sve popisati:
[table]
111 112 113 114 115 116
121 122 123 124 125 126
131 132 133 134 135 136
141 142 143 144 145 146
151 152 153 154 155 156
161 162 163 164 165 [color=green][b]166[/b][/color]
211 212 213 214 215 216
221 222 223 224 225 226
231 232 233 234 235 236
241 242 243 244 245 246
251 252 253 254 255 256
261 262 263 264 265 [color=green][b]266[/b][/color]
311 312 313 314 315 316
321 322 323 324 325 326
331 332 333 334 335 336
341 342 343 344 345 346
351 352 353 354 355 356
361 362 363 364 365 [color=green][b]366[/b][/color]
411 412 413 414 415 416
421 422 423 424 425 426
431 432 433 434 435 436
441 442 443 444 445 446
451 452 453 454 455 456
461 462 463 464 465 [color=green][b]466[/b][/color]
511 512 513 514 515 516
521 522 523 524 525 526
531 532 533 534 535 536
541 542 543 544 545 546
551 552 553 554 555 556
561 562 563 564 565 [color=green][b]566[/b][/color]
611 612 613 614 615 [color=green][b]616[/b][/color]
621 622 623 624 625 [color=green][b]626[/b][/color]
631 632 633 634 635 [color=green][b]636[/b][/color]
641 642 643 644 645 [color=green][b]646[/b][/color]
651 652 653 654 655 [color=green][b]656[/b][/color]
[color=green][b]661[/b][/color] [color=green][b]662[/b][/color] [color=green][b]663[/b][/color] [color=green][b]664[/b][/color] [color=green][b]665[/b][/color] 666[/table]
Koliko ima onih koji ti odgovaraju (boldani zeleni)? :D
Ako mislis da sam krivo popisao svih [latex]6^3[/latex] mogucnosti, probaj ih sam popisati tako da ispadne samo 5 "povoljnih". ;)
P.S. Ne brini, nisam ja ovo gore "na ruke" radio:[code:1]perl -e 'for$i(1..6){for$j(1..6){print join(" ", map{$x="$i$j$_"; $x = "[color=green][b]".$x."[/b][/color]" if $x =~ /^(66[^6]|6[^6]6|[^6]66)$/; $x}(1..6)), "\n";}}'[/code:1]8)
Ali ti racunas ukupni broj mogucnosti kao 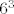 , sto znaci da razlikujes kocke (bilo kao prvu, drugu i trecu, bilo kao prvo, drugo i trece bacanje iste kocke). Dakle, tebi je abc razlicito bacanje od bca, pa moras razlikovati kocke. 
Ajmo sve popisati:
| 111 | 112 | 113 | 114 | 115 | 116 | | 121 | 122 | 123 | 124 | 125 | 126 | | 131 | 132 | 133 | 134 | 135 | 136 | | 141 | 142 | 143 | 144 | 145 | 146 | | 151 | 152 | 153 | 154 | 155 | 156 | | 161 | 162 | 163 | 164 | 165 | 166 | | 211 | 212 | 213 | 214 | 215 | 216 | | 221 | 222 | 223 | 224 | 225 | 226 | | 231 | 232 | 233 | 234 | 235 | 236 | | 241 | 242 | 243 | 244 | 245 | 246 | | 251 | 252 | 253 | 254 | 255 | 256 | | 261 | 262 | 263 | 264 | 265 | 266 | | 311 | 312 | 313 | 314 | 315 | 316 | | 321 | 322 | 323 | 324 | 325 | 326 | | 331 | 332 | 333 | 334 | 335 | 336 | | 341 | 342 | 343 | 344 | 345 | 346 | | 351 | 352 | 353 | 354 | 355 | 356 | | 361 | 362 | 363 | 364 | 365 | 366 | | 411 | 412 | 413 | 414 | 415 | 416 | | 421 | 422 | 423 | 424 | 425 | 426 | | 431 | 432 | 433 | 434 | 435 | 436 | | 441 | 442 | 443 | 444 | 445 | 446 | | 451 | 452 | 453 | 454 | 455 | 456 | | 461 | 462 | 463 | 464 | 465 | 466 | | 511 | 512 | 513 | 514 | 515 | 516 | | 521 | 522 | 523 | 524 | 525 | 526 | | 531 | 532 | 533 | 534 | 535 | 536 | | 541 | 542 | 543 | 544 | 545 | 546 | | 551 | 552 | 553 | 554 | 555 | 556 | | 561 | 562 | 563 | 564 | 565 | 566 | | 611 | 612 | 613 | 614 | 615 | 616 | | 621 | 622 | 623 | 624 | 625 | 626 | | 631 | 632 | 633 | 634 | 635 | 636 | | 641 | 642 | 643 | 644 | 645 | 646 | | 651 | 652 | 653 | 654 | 655 | 656 | | 661 | 662 | 663 | 664 | 665 | 666 |
Koliko ima onih koji ti odgovaraju (boldani zeleni)?
Ako mislis da sam krivo popisao svih 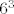mogucnosti, probaj ih sam popisati tako da ispadne samo 5 "povoljnih". 
P.S. Ne brini, nisam ja ovo gore "na ruke" radio: | Kod: | | perl -e 'for$i(1..6){for$j(1..6){print join(" ", map{$x="$i$j$_"; $x = "[color=green][b]".$x."[/b][/color]" if $x =~ /^(66[^6]|6[^6]6|[^6]66)$/; $x}(1..6)), "\n";}}' |
_________________ U pravilu ignoriram pitanja u krivim topicima i kodove koji nisu u [code]...[/code] blokovima.
Takodjer, OBJASNITE sto vas muci! "Sto mi je krivo?", bez opisa u cemu je problem, rijetko ce zadobiti moju paznju. |
|
| [Vrh] |
|
Fazh
Forumaš s poteškoćama u pisanju
Pridružen/a: 09. 11. 2008. (22:51:55)
Postovi: (D)16
Lokacija: Jucer
|
|
| [Vrh] |
|
Saf
Forumski umjetnik
Pridružen/a: 10. 06. 2005. (21:55:28)
Postovi: (1B0)16
Spol:
Lokacija: Zagreb
|
|
| [Vrh] |
|
vsego
Site Admin
Pridružen/a: 06. 10. 2002. (22:07:09)
Postovi: (3560)16
Spol:
Lokacija: /sbin/init
|
| Postano: 20:01 pet, 25. 6. 2010 Naslov: |
|
|
|
Zaboravio si slucaj u kojem dobijes sesticu samo u prvom bacanju. Nema tu BSO, kad ti onih 36 pokriva i (6,y) i (x,6).
To se obicno radi preko [url=http://en.wikipedia.org/wiki/Inclusion–exclusion_principle]FUI (formula ukljucivanja i iskljucivanja)[/url]. Opcenito (za vise od dvije-tri kocke) je tako lakse.
Zaboravio si slucaj u kojem dobijes sesticu samo u prvom bacanju. Nema tu BSO, kad ti onih 36 pokriva i (6,y) i (x,6).
To se obicno radi preko FUI (formula ukljucivanja i iskljucivanja). Opcenito (za vise od dvije-tri kocke) je tako lakse.
_________________ U pravilu ignoriram pitanja u krivim topicima i kodove koji nisu u [code]...[/code] blokovima.
Takodjer, OBJASNITE sto vas muci! "Sto mi je krivo?", bez opisa u cemu je problem, rijetko ce zadobiti moju paznju. |
|
| [Vrh] |
|
Saf
Forumski umjetnik
Pridružen/a: 10. 06. 2005. (21:55:28)
Postovi: (1B0)16
Spol:
Lokacija: Zagreb
|
|
| [Vrh] |
|
behemont
Forumaš(ica)
Pridružen/a: 12. 02. 2008. (21:21:19)
Postovi: (124)16
Spol:
|
|
| [Vrh] |
|
vsego
Site Admin
Pridružen/a: 06. 10. 2002. (22:07:09)
Postovi: (3560)16
Spol:
Lokacija: /sbin/init
|
| Postano: 1:43 pon, 28. 6. 2010 Naslov: |
|
|
|
[quote="Saf"]ukupna vjerojatnost: 1/36 + 5/36 + 5/36 = 11/36
jel to točno?[/quote]
To bi ipak, za provjeru, trebao znati iskodirati u C-u. :P Evo ti u PERL-u (isto kao u C-u, samo kompaktnije):
[code:1]$ perl -e 'for$i(1..6){for$j(1..6){print++$c,". ($i,$j)\n"if$i==6||$j==6;}};'
1. (1,6)
2. (2,6)
3. (3,6)
4. (4,6)
5. (5,6)
6. (6,1)
7. (6,2)
8. (6,3)
9. (6,4)
10. (6,5)
11. (6,6)[/code:1]
| Saf (napisa): | ukupna vjerojatnost: 1/36 + 5/36 + 5/36 = 11/36
jel to točno? |
To bi ipak, za provjeru, trebao znati iskodirati u C-u.  Evo ti u PERL-u (isto kao u C-u, samo kompaktnije):
| Kod: | $ perl -e 'for$i(1..6){for$j(1..6){print++$c,". ($i,$j)\n"if$i==6||$j==6;}};'
1. (1,6)
2. (2,6)
3. (3,6)
4. (4,6)
5. (5,6)
6. (6,1)
7. (6,2)
8. (6,3)
9. (6,4)
10. (6,5)
11. (6,6) |
_________________ U pravilu ignoriram pitanja u krivim topicima i kodove koji nisu u [code]...[/code] blokovima.
Takodjer, OBJASNITE sto vas muci! "Sto mi je krivo?", bez opisa u cemu je problem, rijetko ce zadobiti moju paznju. |
|
| [Vrh] |
|
|
