| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
Tomislav
Forumaš(ica)

Pridružen/a: 04. 10. 2010. (20:18:25)
Postovi: (181)16
Spol: 
|
|
| [Vrh] |
|
888
Forumaš(ica)

Pridružen/a: 09. 10. 2010. (18:26:14)
Postovi: (29)16
|
|
| [Vrh] |
|
frutabella
Forumaš(ica)

Pridružen/a: 09. 10. 2010. (16:35:36)
Postovi: (24E)16
|
|
| [Vrh] |
|
kenny
Petica iz zalaganja


Pridružen/a: 28. 03. 2003. (09:18:36)
Postovi: (3B7)16
Spol: 
Lokacija: ...somewhere over the rainbow...
|
|
| [Vrh] |
|
A-tom
Forumaš(ica)

Pridružen/a: 18. 05. 2010. (22:18:01)
Postovi: (AB)16
Spol: 
|
|
| [Vrh] |
|
medonja
Forumaš(ica)


Pridružen/a: 20. 10. 2009. (17:01:04)
Postovi: (45)16
|
 Postano: 16:47 sri, 13. 10. 2010 Naslov: Postano: 16:47 sri, 13. 10. 2010 Naslov: |
    |
|
|
Zamolila bi nekog, tko je voljan da napiše postupke rješavanja za 6., 10., 13.(c) i 15(a). Možda nekima ovi zadaci jesu trivijalni ali ima nas koje muče... :oops: Hvala..
http://web.math.hr/nastava/analiza/files/ma1-zadaca1.pdf
[size=9][color=#999999]Added after 3 minutes:[/color][/size]
[quote="888"]Imam pitanje u vezi zadatka 13 (trigonometrija mi nije jača strana :( ) , ako bi mi netko mogao pokazati kako riješiti, barem neke hintove.. dakle, pod (a) sin(Πx)>cos(π[latex]\sqrt{x}[/latex])
i pod (b)sin(2Πcosx)>0[/quote]
b)
sin(2(pi)cosx)>sin(pi)
2(pi)cosx>(pi)
2cosx>0
cosx>cos(pi/2)
x>(pi/2)
..a) ne znam :cry:
Zamolila bi nekog, tko je voljan da napiše postupke rješavanja za 6., 10., 13.(c) i 15(a). Možda nekima ovi zadaci jesu trivijalni ali ima nas koje muče...  Hvala.. Hvala..
http://web.math.hr/nastava/analiza/files/ma1-zadaca1.pdf
Added after 3 minutes:
| 888 (napisa): | Imam pitanje u vezi zadatka 13 (trigonometrija mi nije jača strana  ) , ako bi mi netko mogao pokazati kako riješiti, barem neke hintove.. dakle, pod (a) sin(Πx)>cos(π ) , ako bi mi netko mogao pokazati kako riješiti, barem neke hintove.. dakle, pod (a) sin(Πx)>cos(π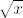 ) )
i pod (b)sin(2Πcosx)>0 |
b)
sin(2(pi)cosx)>sin(pi)
2(pi)cosx>(pi)
2cosx>0
cosx>cos(pi/2)
x>(pi/2)
..a) ne znam 
|
|
| [Vrh] |
|
Tomislav
Forumaš(ica)

Pridružen/a: 04. 10. 2010. (20:18:25)
Postovi: (181)16
Spol: 
|
 Postano: 17:18 sri, 13. 10. 2010 Naslov: Postano: 17:18 sri, 13. 10. 2010 Naslov: |
    |
|
|
[quote="medonja"]Zamolila bi nekog, tko je voljan da napiše postupke rješavanja za 6., 10., 13.(c) i 15(a). Možda nekima ovi zadaci jesu trivijalni ali ima nas koje muče... :oops: Hvala..
http://web.math.hr/nastava/analiza/files/ma1-zadaca1.pdf
[size=9][color=#999999]Added after 3 minutes:[/color][/size]
[quote="888"]Imam pitanje u vezi zadatka 13 (trigonometrija mi nije jača strana :( ) , ako bi mi netko mogao pokazati kako riješiti, barem neke hintove.. dakle, pod (a) sin(Πx)>cos(π[latex]\sqrt{x}[/latex])
i pod (b)sin(2Πcosx)>0[/quote]
b)
sin(2(pi)cosx)>sin(pi)
2(pi)cosx>(pi)
2cosx>0
cosx>cos(pi/2)
x>(pi/2)[/quote]
Ako uvrstim [latex]x=\frac{5 \pi}{9}[/latex], imamo:
[latex]sin(2\pi cos(\frac{5 \pi}{9}))=-0.8871183..[/latex] što nije [latex]> 0[/latex]
| medonja (napisa): | Zamolila bi nekog, tko je voljan da napiše postupke rješavanja za 6., 10., 13.(c) i 15(a). Možda nekima ovi zadaci jesu trivijalni ali ima nas koje muče...  Hvala.. Hvala..
http://web.math.hr/nastava/analiza/files/ma1-zadaca1.pdf
Added after 3 minutes:
| 888 (napisa): | Imam pitanje u vezi zadatka 13 (trigonometrija mi nije jača strana  ) , ako bi mi netko mogao pokazati kako riješiti, barem neke hintove.. dakle, pod (a) sin(Πx)>cos(π ) , ako bi mi netko mogao pokazati kako riješiti, barem neke hintove.. dakle, pod (a) sin(Πx)>cos(π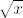 ) )
i pod (b)sin(2Πcosx)>0 |
b)
sin(2(pi)cosx)>sin(pi)
2(pi)cosx>(pi)
2cosx>0
cosx>cos(pi/2)
x>(pi/2) |
Ako uvrstim 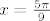 , imamo: , imamo:
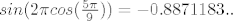 što nije što nije 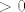
|
|
| [Vrh] |
|
medonja
Forumaš(ica)


Pridružen/a: 20. 10. 2009. (17:01:04)
Postovi: (45)16
|
|
| [Vrh] |
|
Tomislav
Forumaš(ica)

Pridružen/a: 04. 10. 2010. (20:18:25)
Postovi: (181)16
Spol: 
|
|
| [Vrh] |
|
medonja
Forumaš(ica)


Pridružen/a: 20. 10. 2009. (17:01:04)
Postovi: (45)16
|
|
| [Vrh] |
|
Bruno^_^
Forumaš(ica)

Pridružen/a: 09. 10. 2010. (20:22:27)
Postovi: (1D)16
|
 Postano: 18:41 sri, 13. 10. 2010 Naslov: Postano: 18:41 sri, 13. 10. 2010 Naslov: |
    |
|
|
[quote]Imam pitanje u vezi zadatka 13 (trigonometrija mi nije jača strana ) , ako bi mi netko mogao pokazati kako riješiti, barem neke hintove.. dakle, pod (a) sin(Πx)>cos(π)
i pod (b)sin(2Πcosx)>0[/quote]
Nema potrebe za ikakvim transformiranjem izraza, s brojevne kružnice je jasno da vrijedi [latex]sin(2 \pi cos(x))>0[/latex] akko [latex]2k \pi < 2 \pi cos(x) < (2k+1)\pi[/latex] za neki [latex]k \in Z[/latex]. Dakle [latex]k < cos(x) < k + \frac{1}{2}[/latex] za [latex]k \in \{-1,0\}[/latex]. Sada samo nađemo sve [latex]x[/latex] za koje to vrijedi i dobivamo rješenja kao uniju :)
Hint za a) napisati sinus kao kosinus (ili obratno), prebaciti na jednu stranu nejednakosti i koristiti formule pretvorbe zbroja u umnožak. Zatim slijedi tedious yet feasible rješavanje nejednakosti. Ne znam da li ima jednostavnijeg rješenja.
| Citat: | Imam pitanje u vezi zadatka 13 (trigonometrija mi nije jača strana ) , ako bi mi netko mogao pokazati kako riješiti, barem neke hintove.. dakle, pod (a) sin(Πx)>cos(π)
i pod (b)sin(2Πcosx)>0 |
Nema potrebe za ikakvim transformiranjem izraza, s brojevne kružnice je jasno da vrijedi 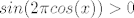 akko akko 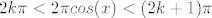 za neki za neki 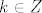 . Dakle . Dakle 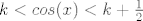 za za 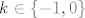 . Sada samo nađemo sve . Sada samo nađemo sve  za koje to vrijedi i dobivamo rješenja kao uniju za koje to vrijedi i dobivamo rješenja kao uniju 
Hint za a) napisati sinus kao kosinus (ili obratno), prebaciti na jednu stranu nejednakosti i koristiti formule pretvorbe zbroja u umnožak. Zatim slijedi tedious yet feasible rješavanje nejednakosti. Ne znam da li ima jednostavnijeg rješenja.
|
|
| [Vrh] |
|
pupi
Forumaš(ica)

Pridružen/a: 20. 12. 2009. (11:03:15)
Postovi: (92)16
Spol: 
|
|
| [Vrh] |
|
mornik
Forumaš(ica)

Pridružen/a: 26. 09. 2009. (06:25:44)
Postovi: (128)16
|
 Postano: 7:13 pet, 22. 10. 2010 Naslov: Postano: 7:13 pet, 22. 10. 2010 Naslov: |
    |
|
|
Da. Zapravo se radi o tome da nas u tom slučaju samo zanima praslika intervala [latex]\[-1,1\][/latex] (vrijednosti manje od [latex]-1[/latex] se ni ne postižu), a to je, dakako, za [latex]\cos[/latex] cijeli [latex]\mathbb{R}[/latex]. Formalno, mogli smo i tražiti [latex]\arccos -1[/latex] i [latex]\arccos 1[/latex], ali kad bismo sve to napisali i dobili neku uniju, vidjeli bismo da je ta unija zapravo cijeli [latex]\mathbb{R}[/latex].
Da. Zapravo se radi o tome da nas u tom slučaju samo zanima praslika intervala 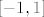 (vrijednosti manje od (vrijednosti manje od  se ni ne postižu), a to je, dakako, za se ni ne postižu), a to je, dakako, za  cijeli cijeli  . Formalno, mogli smo i tražiti . Formalno, mogli smo i tražiti  i i 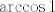 , ali kad bismo sve to napisali i dobili neku uniju, vidjeli bismo da je ta unija zapravo cijeli , ali kad bismo sve to napisali i dobili neku uniju, vidjeli bismo da je ta unija zapravo cijeli  . .
|
|
| [Vrh] |
|
pupi
Forumaš(ica)

Pridružen/a: 20. 12. 2009. (11:03:15)
Postovi: (92)16
Spol: 
|
|
| [Vrh] |
|
|











