| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
CROmpir
Forumaš(ica)

Pridružen/a: 15. 09. 2009. (18:27:06)
Postovi: (B3)16
|
|
| [Vrh] |
|
pmli
Forumaš(ica)

Pridružen/a: 09. 11. 2009. (12:03:05)
Postovi: (2C8)16
Spol: 
|
 Postano: 17:43 uto, 14. 12. 2010 Naslov: Re: 3. zadatak iz zadace Postano: 17:43 uto, 14. 12. 2010 Naslov: Re: 3. zadatak iz zadace |
    |
|
|
Bio bih naprosto oduševljen kad bi ljudi koji ne koriste latex znali koristiti zagrade. To bi pokazalo da se sjećaju osnovne škole, a to iznimno poštujem. :D ;)
[quote="CROmpir"]Ispitajte ogranicenost nizova:
a). (n^2) / (n^2 +1)
b). (-1)^n * n^2) / n + 4
c). n^3 / n +1
Moze li mi netko pomoci oko ovih zadataka? Problem je da znam tj. uocljivo je da su neki ograniceni al kako to racunski odrediti? Koje je prihvatljivo rjesenje kao zadaca?[/quote]
Traži se ispitati ograničenost, što bi valjda trebalo značiti da je potrebno odrediti je li neki niz ograničen odozdo i/ili odozgo, a ne i odrediti donju i gornju među. :?
Niz u a) je konvergentan, pa je ograničen (odozdo i odozgo).
Niz u b) ima jedan podniz koji divergira u [latex]-\infty[/latex] i jedan koji divergira u [latex]+\infty[/latex]. Dakle, nije ograničen ni odozdo ni odozgo.
Niz u c) divergira u [latex]+\infty[/latex], pa nije ograničen odozgo, ali je ograničen odozdo (to je i očito iz toga što je niz rastući).
[quote="CROmpir"]I moze pomoc oko 18 zadatka? To je treca zadaca... Unaprijed hvala na pomoci.[/quote]
Indukcija.
Bio bih naprosto oduševljen kad bi ljudi koji ne koriste latex znali koristiti zagrade. To bi pokazalo da se sjećaju osnovne škole, a to iznimno poštujem.  
| CROmpir (napisa): | Ispitajte ogranicenost nizova:
a). (n^2) / (n^2 +1)
b). (-1)^n * n^2) / n + 4
c). n^3 / n +1
Moze li mi netko pomoci oko ovih zadataka? Problem je da znam tj. uocljivo je da su neki ograniceni al kako to racunski odrediti? Koje je prihvatljivo rjesenje kao zadaca? |
Traži se ispitati ograničenost, što bi valjda trebalo značiti da je potrebno odrediti je li neki niz ograničen odozdo i/ili odozgo, a ne i odrediti donju i gornju među. 
Niz u a) je konvergentan, pa je ograničen (odozdo i odozgo).
Niz u b) ima jedan podniz koji divergira u 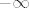 i jedan koji divergira u i jedan koji divergira u  . Dakle, nije ograničen ni odozdo ni odozgo. . Dakle, nije ograničen ni odozdo ni odozgo.
Niz u c) divergira u  , pa nije ograničen odozgo, ali je ograničen odozdo (to je i očito iz toga što je niz rastući). , pa nije ograničen odozgo, ali je ograničen odozdo (to je i očito iz toga što je niz rastući).
| CROmpir (napisa): | | I moze pomoc oko 18 zadatka? To je treca zadaca... Unaprijed hvala na pomoci. |
Indukcija.
|
|
| [Vrh] |
|
CROmpir
Forumaš(ica)

Pridružen/a: 15. 09. 2009. (18:27:06)
Postovi: (B3)16
|
|
| [Vrh] |
|
pmli
Forumaš(ica)

Pridružen/a: 09. 11. 2009. (12:03:05)
Postovi: (2C8)16
Spol: 
|
 Postano: 21:32 uto, 14. 12. 2010 Naslov: Postano: 21:32 uto, 14. 12. 2010 Naslov: |
    |
|
|
Ne vidim što se ima još za raspisati, osim ako te zanima kako odrediti neke međe.
Na predavanjima ste pokazali da ako je niz konvergentan, onda je ograničen. U a) očito je da je 0 donja, a 1 gornja međa. Ako baš želiš infimum i supremum, treba otkriti raste li ili pada taj niz.
Za b), označimo [latex]\displaystyle a_n = (-1)^n \frac{n^2}{n + 4}[/latex]. Vidimo da je [latex]\displaystyle a_{2 n} = \frac{4 n^2}{2 n + 4} \to +\infty[/latex] i [latex]\displaystyle a_{2 n - 1} = -\frac{(2 n - 1)^2}{2 n - 3} \to -\infty[/latex]. Nije teško pokazati da taj niz nema ni donju ni gornju među. Dokažimo, npr. da nema donju. Pretpostavimo suprotno, tj. da postoji [latex]M > 0[/latex] td. [latex]-M \leq a_n[/latex], za svaki [latex]n \in \mathbb{N}[/latex]. Kako [latex]a_{2 n - 1} \to -\infty[/latex], po definiciji slijedi da postoji neki [latex]n_0 \in \mathbb{N}[/latex] td. [latex]a_{2 n_0 - 1} < -M[/latex] (zapravo, u definiciji divergencije u [latex]-\infty[/latex] se zahtjeva više, ali ovo nam je dovoljno). Kontradikcija!
U c) niz divergira u [latex]+\infty[/latex], pa se slično kao gore može pokazati da onda nema gornju među. Nije teško za vidjeti da je 0 jedna donja međa.
Ne vidim što se ima još za raspisati, osim ako te zanima kako odrediti neke međe.
Na predavanjima ste pokazali da ako je niz konvergentan, onda je ograničen. U a) očito je da je 0 donja, a 1 gornja međa. Ako baš želiš infimum i supremum, treba otkriti raste li ili pada taj niz.
Za b), označimo 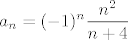 . Vidimo da je . Vidimo da je 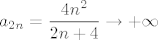 i i 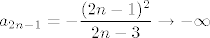 . Nije teško pokazati da taj niz nema ni donju ni gornju među. Dokažimo, npr. da nema donju. Pretpostavimo suprotno, tj. da postoji . Nije teško pokazati da taj niz nema ni donju ni gornju među. Dokažimo, npr. da nema donju. Pretpostavimo suprotno, tj. da postoji 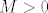 td. td. 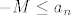 , za svaki , za svaki  . Kako . Kako 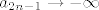 , po definiciji slijedi da postoji neki , po definiciji slijedi da postoji neki  td. td. 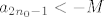 (zapravo, u definiciji divergencije u (zapravo, u definiciji divergencije u 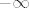 se zahtjeva više, ali ovo nam je dovoljno). Kontradikcija! se zahtjeva više, ali ovo nam je dovoljno). Kontradikcija!
U c) niz divergira u  , pa se slično kao gore može pokazati da onda nema gornju među. Nije teško za vidjeti da je 0 jedna donja međa. , pa se slično kao gore može pokazati da onda nema gornju među. Nije teško za vidjeti da je 0 jedna donja međa.
|
|
| [Vrh] |
|
|






