|
@A-tom
Eto, to sto je Ivanaa rekla :)
znaci samo izlucujes i grupiras u produkt... a 2 iz nazivnika se pokrati s 2 uz kosinuse, vjerojatno te to buni.
Samo da se zna, ja jesam koristio adicijske formule, ovo da se predje iz sume kosinusa u produkt je za mene voodoo magija :D:D
lijepo je vidjeti studente koji to znaju koristiti :D
@rimidalv1991
evo 2. grupe...
bas da znam sluzbeni postupak, ne znam... ali nekakvo rjesenje imam:
infimum dobijemo jeftino, fiksiramo ili m ili n i ovog drugog pustimo u beskonacnost pa dobijemo 0... skup ocito sadrzi nenegativne elemente pa je taj infimum "dobar" :)
e sad supremum je malo tezi za pronaci... barem ja neznam neku opcu metodu bez nekog petljanja...
[latex]S = \left\{ \displaystyle\frac{1}{\frac{m}{n} + 4\cdot\frac{n}{m}+3 } : m,n\in\mathbb{N}\right\}[/latex]
Sad je ocito da zelimo da nam nazivnik bude sto manji pa bi htjeli naci infimum tog skupa. Buduci da ako pustimo ili m ili n u beskonacnost dobit cemo da nam izraz tezi u beskonacnost pa se ocito infimum postize za konkretne m i n, odnosno infimum je minimum.
Sad dolazimo do gadnijeg dijela... neka je C nas minimum, vrijedi:
[latex]\displaystyle\frac{4n}{m} + \displaystyle\frac{m}{n} + 3 \geq C \Leftrightarrow \displaystyle\frac{4}{m} n^2 + (3 - C)n + m \geq 0[/latex]
Opravdanje za mnozenje s n bi bilo da je rijec o prirodnom broju, pa nam nece "uzbuniti" nejednakost :D. Buduci da zelimo da nam je nejednakost "dobra" za proizvoljne m i n, diskriminanta kvadratne jednadzbe po n bi nam trebala biti jednaka 0. Naime, za diskriminantu vecu od 0 bi imali m, n takve da je pocetni izraz manji od C, a za diskriminantu manju od 0 izraz nikad ne bi postigao vrijednost C. Dakle,
[latex](3 - C)^2 - 4\cdot\frac{4}{m}\cdot m = 0 \implies (3 - C)^2 = 16[/latex]
Dobivamo [latex]C_1 = -1, C_2 = 7[/latex]. Ocito da [latex]C_1[/latex] ne dolazi u obzir jer je izraz strogo pozitivan, rjesenje je [latex]C = 7[/latex], pa bi supremum skupa trebao biti [latex]\frac{1}{7}[/latex]. Provjerimo:
[latex]\displaystyle\frac{mn}{m^2+4n^2+3mn} \leq \displaystyle\frac{1}{7}[/latex]
[latex]\Leftrightarrow m^2 + 4n^2 + 3mn \geq 7mn[/latex]
[latex]\Leftrightarrow m^2 - 4mn + 4n^2 \geq 0[/latex]
[latex]\Leftrightarrow (m-2n)^2 \geq 0[/latex]
Sto ocito vrijedi za sve m, n. Iz ovoga vidimo i kad se supremum postize: [latex]m = 2n[/latex].
Dakle, dobili smo sto smo htjeli: [latex]\boxed{\sup S = \frac{1}{7}, \quad\inf S = 0}[/latex]
PS vjerojatno je to vec netko negdje rjesio na "prijatniji" nacin :D:D
EDIT:
@zbunjena
upravu si, mozes izracunati infimum i supremum toga pa onda uzeti najvece cijelo... s tim da to moras opravdati cinjenicom da je najvece cijelo rastuca funkcija :)
@A-tom
Eto, to sto je Ivanaa rekla 
znaci samo izlucujes i grupiras u produkt... a 2 iz nazivnika se pokrati s 2 uz kosinuse, vjerojatno te to buni.
Samo da se zna, ja jesam koristio adicijske formule, ovo da se predje iz sume kosinusa u produkt je za mene voodoo magija  
lijepo je vidjeti studente koji to znaju koristiti 
@rimidalv1991
evo 2. grupe...
bas da znam sluzbeni postupak, ne znam... ali nekakvo rjesenje imam:
infimum dobijemo jeftino, fiksiramo ili m ili n i ovog drugog pustimo u beskonacnost pa dobijemo 0... skup ocito sadrzi nenegativne elemente pa je taj infimum "dobar" 
e sad supremum je malo tezi za pronaci... barem ja neznam neku opcu metodu bez nekog petljanja...
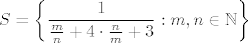
Sad je ocito da zelimo da nam nazivnik bude sto manji pa bi htjeli naci infimum tog skupa. Buduci da ako pustimo ili m ili n u beskonacnost dobit cemo da nam izraz tezi u beskonacnost pa se ocito infimum postize za konkretne m i n, odnosno infimum je minimum.
Sad dolazimo do gadnijeg dijela... neka je C nas minimum, vrijedi:
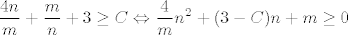
Opravdanje za mnozenje s n bi bilo da je rijec o prirodnom broju, pa nam nece "uzbuniti" nejednakost  . Buduci da zelimo da nam je nejednakost "dobra" za proizvoljne m i n, diskriminanta kvadratne jednadzbe po n bi nam trebala biti jednaka 0. Naime, za diskriminantu vecu od 0 bi imali m, n takve da je pocetni izraz manji od C, a za diskriminantu manju od 0 izraz nikad ne bi postigao vrijednost C. Dakle, . Buduci da zelimo da nam je nejednakost "dobra" za proizvoljne m i n, diskriminanta kvadratne jednadzbe po n bi nam trebala biti jednaka 0. Naime, za diskriminantu vecu od 0 bi imali m, n takve da je pocetni izraz manji od C, a za diskriminantu manju od 0 izraz nikad ne bi postigao vrijednost C. Dakle,
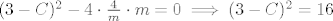
Dobivamo 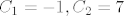 . Ocito da . Ocito da 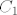 ne dolazi u obzir jer je izraz strogo pozitivan, rjesenje je ne dolazi u obzir jer je izraz strogo pozitivan, rjesenje je 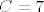 , pa bi supremum skupa trebao biti , pa bi supremum skupa trebao biti 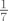 . Provjerimo: . Provjerimo:
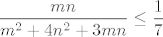

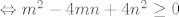
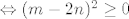
Sto ocito vrijedi za sve m, n. Iz ovoga vidimo i kad se supremum postize: 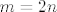 . .
Dakle, dobili smo sto smo htjeli: 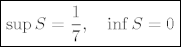
PS vjerojatno je to vec netko negdje rjesio na "prijatniji" nacin  
EDIT:
@zbunjena
upravu si, mozes izracunati infimum i supremum toga pa onda uzeti najvece cijelo... s tim da to moras opravdati cinjenicom da je najvece cijelo rastuca funkcija 
|







