| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
smajl
Forumaš(ica)

Pridružen/a: 02. 01. 2010. (12:59:23)
Postovi: (EB)16
Spol: 
Lokacija: Zagreb
|
|
| [Vrh] |
|
kikyca
Forumaš(ica)

Pridružen/a: 13. 10. 2009. (18:45:07)
Postovi: (32)16
Spol: 
|
|
| [Vrh] |
|
eve
Forumaš(ica)

Pridružen/a: 13. 07. 2009. (23:07:06)
Postovi: (192)16
Spol: 
|
|
| [Vrh] |
|
kikyca
Forumaš(ica)

Pridružen/a: 13. 10. 2009. (18:45:07)
Postovi: (32)16
Spol: 
|
|
| [Vrh] |
|
eve
Forumaš(ica)

Pridružen/a: 13. 07. 2009. (23:07:06)
Postovi: (192)16
Spol: 
|
|
| [Vrh] |
|
Lafiel
Forumaš(ica)


Pridružen/a: 26. 09. 2007. (09:56:59)
Postovi: (153)16
Spol: 
|
|
| [Vrh] |
|
ananas
Forumaš(ica)

Pridružen/a: 28. 10. 2009. (17:56:24)
Postovi: (34)16
|
|
| [Vrh] |
|
Lepi91
Forumaš(ica)


Pridružen/a: 15. 09. 2010. (15:22:23)
Postovi: (C8)16
Spol: 
|
|
| [Vrh] |
|
kikzmyster
Forumaš(ica)

Pridružen/a: 14. 10. 2010. (13:35:08)
Postovi: (72)16
Spol: 
|
 Postano: 20:15 pon, 23. 1. 2012 Naslov: Postano: 20:15 pon, 23. 1. 2012 Naslov: |
    |
|
|
5. zad.
izmnozi ovaj izraz u brojniku, znaci imamo [latex]\displaystyle 1 - 6x^2 + 12 x^4 - 8x^6[/latex] u brojniku. sad promatramo 4 razlomka, svaki razvijamo u red, i onda dobivene redove zbrojimo. npr, za razviti [latex]\displaystyle \frac{1}{(1-x)^5}[/latex] moramo derivirat [latex]\displaystyle \frac{1}{1-x
}[/latex] cetiri puta, i jos podijelit sa 24. [latex]\displaystyle \frac{1}{1-x} = \sum_{n=0}^{\infty}x^n[/latex] pa je [latex]\displaystyle \frac{1}{(1-x)^5} = \frac{1}{24}\sum_{n=4}^{\infty}n(n-1)(n-2)(n-3)x^{n-4} = \sum_{n=0}^{\infty}(n+1)(n+2)(n+3)(n+4)x^n [/latex]. sad i ostala tri razlomka razvijemo u red pomocu ovoga, npr. [latex]\displaystyle \frac{6x^2}{(1-x)^5} [/latex] je ovo gore puta 6x^2. tako dobijemo 4 reda i samo ih zbrojimo, i onda citamo kako izgleda koeficijent uz x^n, to je [latex]\displaystyle a_n [/latex]
[size=9][color=#999999]Added after 1 minutes:[/color][/size]
tek sad vidio da je ovo bilo pitano prosle godine... nema veze, nece nikome skodit :D
5. zad.
izmnozi ovaj izraz u brojniku, znaci imamo 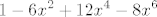 u brojniku. sad promatramo 4 razlomka, svaki razvijamo u red, i onda dobivene redove zbrojimo. npr, za razviti u brojniku. sad promatramo 4 razlomka, svaki razvijamo u red, i onda dobivene redove zbrojimo. npr, za razviti 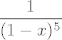 moramo derivirat moramo derivirat 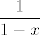 cetiri puta, i jos podijelit sa 24. cetiri puta, i jos podijelit sa 24. 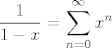 pa je pa je 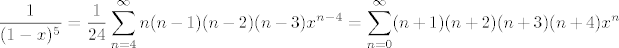 . sad i ostala tri razlomka razvijemo u red pomocu ovoga, npr. . sad i ostala tri razlomka razvijemo u red pomocu ovoga, npr. 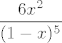 je ovo gore puta 6x^2. tako dobijemo 4 reda i samo ih zbrojimo, i onda citamo kako izgleda koeficijent uz x^n, to je je ovo gore puta 6x^2. tako dobijemo 4 reda i samo ih zbrojimo, i onda citamo kako izgleda koeficijent uz x^n, to je 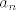
Added after 1 minutes:
tek sad vidio da je ovo bilo pitano prosle godine... nema veze, nece nikome skodit 
|
|
| [Vrh] |
|
Lepi91
Forumaš(ica)


Pridružen/a: 15. 09. 2010. (15:22:23)
Postovi: (C8)16
Spol: 
|
|
| [Vrh] |
|
marsupial
Forumaš(ica)

Pridružen/a: 09. 01. 2012. (22:46:33)
Postovi: (63)16
Spol: 
|
|
| [Vrh] |
|
krcko
Forumaš nagrađen za životno djelo


Pridružen/a: 07. 10. 2002. (15:57:59)
Postovi: (18B3)16
|
|
| [Vrh] |
|
Lepi91
Forumaš(ica)


Pridružen/a: 15. 09. 2010. (15:22:23)
Postovi: (C8)16
Spol: 
|
|
| [Vrh] |
|
markos
Forumaš(ica)
Pridružen/a: 20. 10. 2010. (20:09:26)
Postovi: (B)16
|
|
| [Vrh] |
|
ceps
Forumaš(ica)

Pridružen/a: 08. 10. 2010. (13:03:07)
Postovi: (13A)16
|
 Postano: 9:38 pet, 27. 1. 2012 Naslov: Postano: 9:38 pet, 27. 1. 2012 Naslov: |
    |
|
|
@markos
Nadam se da se sjećaš definicije particije, ako ne: http://en.wikipedia.org/wiki/Partition_of_a_set podsjeti se :D
=> smjer
Neka je f:A -> B surjekcija.
[latex]f^{-1}(y) [/latex] je neprazan skup za svaki [latex]y \in B[/latex] - trivijalno, slijedi iz definicije same fje.
[latex]f^{-1}(y) \cap f^{-1}(z) = \emptyset, \forall y, z \in B, y \neq z[/latex] opet slijedi iz svojstva funkcije:
pretpostavi suprotno, onda bi slijedilo da postoji [latex]x \in A[/latex] t.d. je f(x) = y i f(x) = z, što je kontradikcija se def. funkcije
[latex]\bigcup_{y \in B} f^{-1}(y) = A[/latex] - to slijedi iz toga što je funkcija surjekcija, opet, ako bi pretpostavio suprotno ispalo bi da postoji y iz B za kojeg ne postoji x iz A t.d. je f(x) = y što je kontradikcija s činjenicom da je f surjekcija
<=
Ide veoma slično, iz svojstava particije zaključuješ da je f surjekcija, obrni smjer u argumentima gore i doći ćeš do toga.
Mislim, ovaj dokaz je na razini EM1 i gotovo je trivijalan - proizlazi čisto iz razumijevanja što je to particija skupa, što znači da je fja surjekcija i iz definicija ta dva pojma.
Probaj si nacrtati par sličica, možda ti pomogne da shvatiš. :)
I reci ako je što ostalo nejasno.
@markos
Nadam se da se sjećaš definicije particije, ako ne: http://en.wikipedia.org/wiki/Partition_of_a_set podsjeti se 
⇒ smjer
Neka je f:A → B surjekcija.
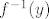 je neprazan skup za svaki je neprazan skup za svaki 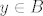 - trivijalno, slijedi iz definicije same fje. - trivijalno, slijedi iz definicije same fje.
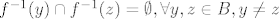 opet slijedi iz svojstva funkcije: opet slijedi iz svojstva funkcije:
pretpostavi suprotno, onda bi slijedilo da postoji 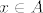 t.d. je f(x) = y i f(x) = z, što je kontradikcija se def. funkcije t.d. je f(x) = y i f(x) = z, što je kontradikcija se def. funkcije
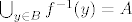 - to slijedi iz toga što je funkcija surjekcija, opet, ako bi pretpostavio suprotno ispalo bi da postoji y iz B za kojeg ne postoji x iz A t.d. je f(x) = y što je kontradikcija s činjenicom da je f surjekcija - to slijedi iz toga što je funkcija surjekcija, opet, ako bi pretpostavio suprotno ispalo bi da postoji y iz B za kojeg ne postoji x iz A t.d. je f(x) = y što je kontradikcija s činjenicom da je f surjekcija
⇐
Ide veoma slično, iz svojstava particije zaključuješ da je f surjekcija, obrni smjer u argumentima gore i doći ćeš do toga.
Mislim, ovaj dokaz je na razini EM1 i gotovo je trivijalan - proizlazi čisto iz razumijevanja što je to particija skupa, što znači da je fja surjekcija i iz definicija ta dva pojma.
Probaj si nacrtati par sličica, možda ti pomogne da shvatiš. 
I reci ako je što ostalo nejasno.
|
|
| [Vrh] |
|
Phoenix
Forumaš(ica)


Pridružen/a: 15. 05. 2010. (18:46:07)
Postovi: (164)16
Sarma: -
|
 Postano: 9:40 pet, 27. 1. 2012 Naslov: Postano: 9:40 pet, 27. 1. 2012 Naslov: |
    |
|
|
[tex]\Rightarrow[/tex] Neka je [tex]f[/tex] surjekcija. Tada [tex](\forall y \in B)(\exists x \in A)x=f^{-1}(y)[/tex] (to je po definiciji surjekcije). To zapravo znači da je skup [tex]f^{-1}(y)[/tex] neprazan za svaki [tex]y[/tex].
Nadalje, za [tex]y_1 \neq y_2[/tex]vrijedi [tex]f^{-1}(y_1) \cap f^{-1}(y_2) = \emptyset[/tex]. U protivnom, postojao bi [tex]x \in A[/tex] koji bi se preslikavao i u [tex]y_1[/tex] i u [tex]y_2[/tex], a to nema smisla jer je [tex]f[/tex] funkcija.
Konačno, [tex]\bigcup_{y \in B}f^{-1}(y)=A[/tex] jer radimo uniju po svim elementima u koje se [tex]x[/tex] iz [tex]A[/tex] može preslikati.
Dakle, skup [tex]\left\{ f^{-1}(y) : y \in B \right\}[/tex] je zaista particija skupa [tex]A[/tex].
[tex]\Leftarrow[/tex] Neka je [tex]\left\{ f^{-1}(y) : y \in B \right\}[/tex] particija od [tex]A[/tex]. Tada je za svaki [tex]y[/tex] iz [tex]B[/tex] skup [tex]f^{-1}(y)[/tex] neprazan, odnosno postoji [tex]x[/tex] iz [tex]A[/tex] takav da vrijedi [tex]f(x)=y[/tex]. Stoga je [tex]f[/tex] surjekcija.
Nadam se da je jasno. :)
[tex]\Rightarrow[/tex] Neka je [tex]f[/tex] surjekcija. Tada [tex](\forall y \in B)(\exists x \in A)x=f^{-1}(y)[/tex] (to je po definiciji surjekcije). To zapravo znači da je skup [tex]f^{-1}(y)[/tex] neprazan za svaki [tex]y[/tex].
Nadalje, za [tex]y_1 \neq y_2[/tex]vrijedi [tex]f^{-1}(y_1) \cap f^{-1}(y_2) = \emptyset[/tex]. U protivnom, postojao bi [tex]x \in A[/tex] koji bi se preslikavao i u [tex]y_1[/tex] i u [tex]y_2[/tex], a to nema smisla jer je [tex]f[/tex] funkcija.
Konačno, [tex]\bigcup_{y \in B}f^{-1}(y)=A[/tex] jer radimo uniju po svim elementima u koje se [tex]x[/tex] iz [tex]A[/tex] može preslikati.
Dakle, skup [tex]\left\{ f^{-1}(y) : y \in B \right\}[/tex] je zaista particija skupa [tex]A[/tex].
[tex]\Leftarrow[/tex] Neka je [tex]\left\{ f^{-1}(y) : y \in B \right\}[/tex] particija od [tex]A[/tex]. Tada je za svaki [tex]y[/tex] iz [tex]B[/tex] skup [tex]f^{-1}(y)[/tex] neprazan, odnosno postoji [tex]x[/tex] iz [tex]A[/tex] takav da vrijedi [tex]f(x)=y[/tex]. Stoga je [tex]f[/tex] surjekcija.
Nadam se da je jasno. 
|
|
| [Vrh] |
|
markos
Forumaš(ica)
Pridružen/a: 20. 10. 2010. (20:09:26)
Postovi: (B)16
|
|
| [Vrh] |
|
|















