| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
kikzmyster
Forumaš(ica)

Pridružen/a: 14. 10. 2010. (13:35:08)
Postovi: (72)16
Spol: 
|
|
| [Vrh] |
|
piccola
Forumaš(ica)

Pridružen/a: 30. 11. 2009. (15:39:50)
Postovi: (D7)16
|
|
| [Vrh] |
|
mornik
Forumaš(ica)

Pridružen/a: 26. 09. 2009. (06:25:44)
Postovi: (128)16
|
 Postano: 21:18 pet, 18. 3. 2011 Naslov: Postano: 21:18 pet, 18. 3. 2011 Naslov: |
    |
|
|
Mislim da je to zadatak koji mori studentsku populaciju već godinama. :D Sad sam ga opet malo raspisivao i imam neke poluopservacije, ali ništa pametno nili, veeoma široko uzimajući pojam ljepote izraza, dovoljno lijepo da bih dobio ikakvu želju dovesti to do kraja na papiru, ako bi uopće išlo... možda netko ima neko lijepo rješenje, znam da ga ja nikad nisam čuo. :oops:
Mislim da je to zadatak koji mori studentsku populaciju već godinama.  Sad sam ga opet malo raspisivao i imam neke poluopservacije, ali ništa pametno nili, veeoma široko uzimajući pojam ljepote izraza, dovoljno lijepo da bih dobio ikakvu želju dovesti to do kraja na papiru, ako bi uopće išlo... možda netko ima neko lijepo rješenje, znam da ga ja nikad nisam čuo. Sad sam ga opet malo raspisivao i imam neke poluopservacije, ali ništa pametno nili, veeoma široko uzimajući pojam ljepote izraza, dovoljno lijepo da bih dobio ikakvu želju dovesti to do kraja na papiru, ako bi uopće išlo... možda netko ima neko lijepo rješenje, znam da ga ja nikad nisam čuo. 
|
|
| [Vrh] |
|
pmli
Forumaš(ica)

Pridružen/a: 09. 11. 2009. (12:03:05)
Postovi: (2C8)16
Spol: 
|
|
| [Vrh] |
|
Togepi
Forumaš(ica)
Pridružen/a: 21. 11. 2010. (14:31:41)
Postovi: (2B)16
|
|
| [Vrh] |
|
pbakic
Forumaš(ica)

Pridružen/a: 05. 10. 2009. (17:48:30)
Postovi: (143)16
Spol: 
|
|
| [Vrh] |
|
piccola
Forumaš(ica)

Pridružen/a: 30. 11. 2009. (15:39:50)
Postovi: (D7)16
|
|
| [Vrh] |
|
kikzmyster
Forumaš(ica)

Pridružen/a: 14. 10. 2010. (13:35:08)
Postovi: (72)16
Spol: 
|
|
| [Vrh] |
|
pbakic
Forumaš(ica)

Pridružen/a: 05. 10. 2009. (17:48:30)
Postovi: (143)16
Spol: 
|
 Postano: 1:32 pon, 21. 3. 2011 Naslov: Postano: 1:32 pon, 21. 3. 2011 Naslov: |
    |
|
|
Definiramo f(x)=tg(x)-x-x^3/3.
Ocito f(0)=0.
Sada deriviramo funkciju i vidimo da raste na intervalu <0,pi/2>:
(zelimo pokazati da je derivacija veca od 0)
[latex]f'(x)= \frac{1}{cos^2(x)} -1 - x^2 = tg^2x - x^2[/latex]
Sad jos treba dokazati tgx > x na zadanom intervalu, a to mozemo jednako kao i gore, derivacijom:
g(x)=tgx-x; g(0)=0.
[latex]g'(x)=\frac{1}{cos^2(x)} -1 \geq 0[/latex], pa imamo da g raste na tom intervalu => veca je od 0. Sada istim zakljuckom (iz f'(0)>=0) dobivamo da f raste, pa je veca od 0 na zadanom intervalu, iz cega zakljucujemo da nasa nejednakost vrijedi.
Definiramo f(x)=tg(x)-x-x^3/3.
Ocito f(0)=0.
Sada deriviramo funkciju i vidimo da raste na intervalu <0,pi/2>:
(zelimo pokazati da je derivacija veca od 0)
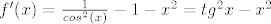
Sad jos treba dokazati tgx > x na zadanom intervalu, a to mozemo jednako kao i gore, derivacijom:
g(x)=tgx-x; g(0)=0.
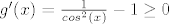 , pa imamo da g raste na tom intervalu ⇒ veca je od 0. Sada istim zakljuckom (iz f'(0)>=0) dobivamo da f raste, pa je veca od 0 na zadanom intervalu, iz cega zakljucujemo da nasa nejednakost vrijedi. , pa imamo da g raste na tom intervalu ⇒ veca je od 0. Sada istim zakljuckom (iz f'(0)>=0) dobivamo da f raste, pa je veca od 0 na zadanom intervalu, iz cega zakljucujemo da nasa nejednakost vrijedi.
|
|
| [Vrh] |
|
kikzmyster
Forumaš(ica)

Pridružen/a: 14. 10. 2010. (13:35:08)
Postovi: (72)16
Spol: 
|
|
| [Vrh] |
|
piccola
Forumaš(ica)

Pridružen/a: 30. 11. 2009. (15:39:50)
Postovi: (D7)16
|
|
| [Vrh] |
|
mornik
Forumaš(ica)

Pridružen/a: 26. 09. 2009. (06:25:44)
Postovi: (128)16
|
 Postano: 7:27 uto, 29. 3. 2011 Naslov: Postano: 7:27 uto, 29. 3. 2011 Naslov: |
    |
|
|
Evo, samo ukratko - ne čini mi se ovo baš kao težak zadatak, tako da bi vjerojatno imalo smisla da kažeš dokle si došla... :)
Neprekidnost, diferencijabilnost i neprekidna diferencijabilnost očito stoje za [latex]x\neq 0[/latex], tako da tu nemamo (imamo? :D) problema. Treba, dakle, još provjeriti kako stvari stoje s nulom.
Pa dobro - prvo gledamo neprekidnost. Specifično, zanima nas postoji li [latex]\displaystyle \lim_{x\to 0}\frac{\sqrt{x+1}-1}{x}[/latex] i iznosi li to [latex]1/2[/latex]. Uistinu, po L'Hôpitalovom pravilu ispada da nas zanima [latex]\displaystyle\frac{1}{2\sqrt{x+1}}[/latex], a to, naravno, ide u [latex]1/2[/latex]. Dakle, neprekidnost imamo, pa ima smisla i tražiti diferencijabilnost.
Zanima nas, stoga, postoji li [latex]\displaystyle \lim_{x\to 0}\frac{\frac{\sqrt{x+1}-1}{x}-\frac{1}{2}}{x}[/latex]. To opet napadnemo L'Hôpitalom i dobivamo da nas zanima limes od [latex]\displaystyle(\frac{\sqrt{x+1}-1}{x})'[/latex], ako on postoji. To je limes od, zapravo, [latex]\displaystyle\frac{2\sqrt{x+1}-2-x}{2x^2}[/latex], a to opet idemo napadati s dva L'Hôpitala i dobivamo [latex]-1/8[/latex] (otprilike, ne jamčim ništa :D). Dakle, pokazali smo da taj limes postoji, pa je funkcija diferencijabilna.
Na kraju bi nas još trebala zanimati neprekidna diferencijabilnost. Zanima nas, dakle, je li [latex]f'(x)=\displaystyle(\frac{\sqrt{x+1}-1}{x})'\to -1/8=f'(0)[/latex]. No, primijeti da smo to upravo pokazali u prethodnom odlomku. Dakle, i to stoji: [latex]f[/latex] je neprekidno diferencijabilna u [latex]0[/latex]. Gotovi! :)
Eto, čini mi se sve razumno, WolframAlpha se čini da se slaže, a ti pitaj ako što nije jasno. :)
Evo, samo ukratko - ne čini mi se ovo baš kao težak zadatak, tako da bi vjerojatno imalo smisla da kažeš dokle si došla... 
Neprekidnost, diferencijabilnost i neprekidna diferencijabilnost očito stoje za 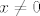 , tako da tu nemamo (imamo? , tako da tu nemamo (imamo?  ) problema. Treba, dakle, još provjeriti kako stvari stoje s nulom. ) problema. Treba, dakle, još provjeriti kako stvari stoje s nulom.
Pa dobro - prvo gledamo neprekidnost. Specifično, zanima nas postoji li 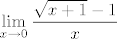 i iznosi li to i iznosi li to 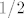 . Uistinu, po L'Hôpitalovom pravilu ispada da nas zanima . Uistinu, po L'Hôpitalovom pravilu ispada da nas zanima 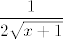 , a to, naravno, ide u , a to, naravno, ide u 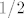 . Dakle, neprekidnost imamo, pa ima smisla i tražiti diferencijabilnost. . Dakle, neprekidnost imamo, pa ima smisla i tražiti diferencijabilnost.
Zanima nas, stoga, postoji li  . To opet napadnemo L'Hôpitalom i dobivamo da nas zanima limes od . To opet napadnemo L'Hôpitalom i dobivamo da nas zanima limes od 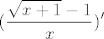 , ako on postoji. To je limes od, zapravo, , ako on postoji. To je limes od, zapravo, 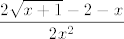 , a to opet idemo napadati s dva L'Hôpitala i dobivamo , a to opet idemo napadati s dva L'Hôpitala i dobivamo 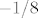 (otprilike, ne jamčim ništa (otprilike, ne jamčim ništa  ). Dakle, pokazali smo da taj limes postoji, pa je funkcija diferencijabilna. ). Dakle, pokazali smo da taj limes postoji, pa je funkcija diferencijabilna.
Na kraju bi nas još trebala zanimati neprekidna diferencijabilnost. Zanima nas, dakle, je li 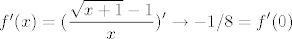 . No, primijeti da smo to upravo pokazali u prethodnom odlomku. Dakle, i to stoji: . No, primijeti da smo to upravo pokazali u prethodnom odlomku. Dakle, i to stoji:  je neprekidno diferencijabilna u je neprekidno diferencijabilna u  . Gotovi! . Gotovi! 
Eto, čini mi se sve razumno, WolframAlpha se čini da se slaže, a ti pitaj ako što nije jasno. 
|
|
| [Vrh] |
|
piccola
Forumaš(ica)

Pridružen/a: 30. 11. 2009. (15:39:50)
Postovi: (D7)16
|
|
| [Vrh] |
|
meda
Forumaš(ica)

Pridružen/a: 09. 01. 2010. (09:29:23)
Postovi: (A0)16
|
|
| [Vrh] |
|
moni_poni
Forumaš(ica)

Pridružen/a: 25. 01. 2010. (19:48:19)
Postovi: (49)16
|
 Postano: 13:02 sri, 30. 3. 2011 Naslov: Postano: 13:02 sri, 30. 3. 2011 Naslov: |
    |
|
|
Zanimaju me zadaci 1.123.b,e,g, 1.126., 1.135., 1.136.
Zanimaju me zadaci 1.123.b,e,g, 1.126., 1.135., 1.136.
|
|
| [Vrh] |
|
meda
Forumaš(ica)

Pridružen/a: 09. 01. 2010. (09:29:23)
Postovi: (A0)16
|
|
| [Vrh] |
|
meda
Forumaš(ica)

Pridružen/a: 09. 01. 2010. (09:29:23)
Postovi: (A0)16
|
|
| [Vrh] |
|
mornik
Forumaš(ica)

Pridružen/a: 26. 09. 2009. (06:25:44)
Postovi: (128)16
|
 Postano: 22:17 sri, 30. 3. 2011 Naslov: Postano: 22:17 sri, 30. 3. 2011 Naslov: |
    |
|
|
[quote="moni_poni"]Zanimaju me zadaci 1.123.b,e,g, 1.126., 1.135., 1.136.[/quote]
Možda da kažeš što te zanima u vezi tih zadataka? :P Provjera rješenja, hintovi, adresa autora, da mu se "zahvališ"? :P Evo čisto nešto što ne bih ni nazvao hintovljem: u 1.136. rekao bih da je stvar prilično straightforward, zar ne: zapravo, čini mi se da postoji samo jedan takav (ovisno o tome što smatramo "upisanim" u kocku, ali i ako uzmemo nešto širu definiciju, i dalje su svi "centrirani" - jasno je ako nacrtaš).
U 1.135. vjerojatno ima smisla da gledaš duljinu tog isječka, pa preko nje napišeš volumen stošca - probao sam sad, mislim da ide, pa reci ako ima problema.
Pretpostavljam da je u 1.123. u svim dijelovima ideja da se pokaže da tvrdnja vrijedi u 0, a da je dalje derivacija razlike lijeve i desne strane pozitivna - u b) se stvar dobiva dosta očito, čini mi se (fizički deriviraš i stvar ti se pokrati), tako da reci koji je problem. U e) je isto tako, pokratiš ono što se može, kvadriraš, i to bi trebalo imati smisla (ja na kraju dobivam [latex]2x^2+2x+1>0[/latex]), a u g) nam zapravo možda bolje ide bez odmah derivacija na početku. Po [url=http://en.wikipedia.org/wiki/Generalized_mean]općenitoj nejednakosti sredina[/url] dovoljno pokazati da je [latex]\sin x + 1/\sin x+\cos x+1/\cos x\geq 3\sqrt{2}[/latex]. To stoji i možeš dobiti relativno ne-teško deriviranjem, pa pitaj ako bude problema (kolega je dobio taj zadatak direktnije, tako da postoji više načina).
U priči s trapezom, stvar je slična kao za stožac - izrazi duljinu druge osnovice i visine kao funkcije u ovisnosti o alfa, a onda bi dalje trebalo ići. :) Evo, nadam se da pomaže, ubio sam se s ovim sada. :D
@Meda: Da, ako dobiješ da su neka rješenja kompleksna, na MA2 se u načelu to tretira isto kao "rješenja nema". :)
| moni_poni (napisa): | | Zanimaju me zadaci 1.123.b,e,g, 1.126., 1.135., 1.136. |
Možda da kažeš što te zanima u vezi tih zadataka?  Provjera rješenja, hintovi, adresa autora, da mu se "zahvališ"? Provjera rješenja, hintovi, adresa autora, da mu se "zahvališ"?  Evo čisto nešto što ne bih ni nazvao hintovljem: u 1.136. rekao bih da je stvar prilično straightforward, zar ne: zapravo, čini mi se da postoji samo jedan takav (ovisno o tome što smatramo "upisanim" u kocku, ali i ako uzmemo nešto širu definiciju, i dalje su svi "centrirani" - jasno je ako nacrtaš). Evo čisto nešto što ne bih ni nazvao hintovljem: u 1.136. rekao bih da je stvar prilično straightforward, zar ne: zapravo, čini mi se da postoji samo jedan takav (ovisno o tome što smatramo "upisanim" u kocku, ali i ako uzmemo nešto širu definiciju, i dalje su svi "centrirani" - jasno je ako nacrtaš).
U 1.135. vjerojatno ima smisla da gledaš duljinu tog isječka, pa preko nje napišeš volumen stošca - probao sam sad, mislim da ide, pa reci ako ima problema.
Pretpostavljam da je u 1.123. u svim dijelovima ideja da se pokaže da tvrdnja vrijedi u 0, a da je dalje derivacija razlike lijeve i desne strane pozitivna - u b) se stvar dobiva dosta očito, čini mi se (fizički deriviraš i stvar ti se pokrati), tako da reci koji je problem. U e) je isto tako, pokratiš ono što se može, kvadriraš, i to bi trebalo imati smisla (ja na kraju dobivam 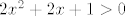 ), a u g) nam zapravo možda bolje ide bez odmah derivacija na početku. Po općenitoj nejednakosti sredina dovoljno pokazati da je ), a u g) nam zapravo možda bolje ide bez odmah derivacija na početku. Po općenitoj nejednakosti sredina dovoljno pokazati da je 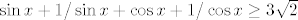 . To stoji i možeš dobiti relativno ne-teško deriviranjem, pa pitaj ako bude problema (kolega je dobio taj zadatak direktnije, tako da postoji više načina). . To stoji i možeš dobiti relativno ne-teško deriviranjem, pa pitaj ako bude problema (kolega je dobio taj zadatak direktnije, tako da postoji više načina).
U priči s trapezom, stvar je slična kao za stožac - izrazi duljinu druge osnovice i visine kao funkcije u ovisnosti o alfa, a onda bi dalje trebalo ići.  Evo, nadam se da pomaže, ubio sam se s ovim sada. Evo, nadam se da pomaže, ubio sam se s ovim sada. 
@Meda: Da, ako dobiješ da su neka rješenja kompleksna, na MA2 se u načelu to tretira isto kao "rješenja nema". 
|
|
| [Vrh] |
|
matijaB
Forumaš(ica)

Pridružen/a: 19. 08. 2010. (09:11:43)
Postovi: (4D)16
|
|
| [Vrh] |
|
Lepi91
Forumaš(ica)


Pridružen/a: 15. 09. 2010. (15:22:23)
Postovi: (C8)16
Spol: 
|
|
| [Vrh] |
|
|











