| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
moni_poni
Forumaš(ica)

Pridružen/a: 25. 01. 2010. (19:48:19)
Postovi: (49)16
|
|
| [Vrh] |
|
meda
Forumaš(ica)

Pridružen/a: 09. 01. 2010. (09:29:23)
Postovi: (A0)16
|
|
| [Vrh] |
|
mornik
Forumaš(ica)

Pridružen/a: 26. 09. 2009. (06:25:44)
Postovi: (128)16
|
|
| [Vrh] |
|
moni_poni
Forumaš(ica)

Pridružen/a: 25. 01. 2010. (19:48:19)
Postovi: (49)16
|
|
| [Vrh] |
|
mornik
Forumaš(ica)

Pridružen/a: 26. 09. 2009. (06:25:44)
Postovi: (128)16
|
 Postano: 8:15 pet, 1. 4. 2011 Naslov: Postano: 8:15 pet, 1. 4. 2011 Naslov: |
    |
|
|
Ajde da vidimo: prvo ćemo napisati [latex]y[/latex] u prihvatljivijem obliku: [latex]y=2+\frac{1}{x-1}[/latex]. To nam sad nije problem derivirati: [latex]y'=-\frac{1}{(x-1)^2}[/latex]. E, i to je manje-više to: jednadžba tangente u točki [latex]x_0[/latex] je dakle [latex]y=-\frac{1}{(x_0-1)^2}x+\frac{x_0}{(x_0-1)^2}+2+\frac{1}{x_0-1}[/latex], ako sam ja to dobro izračunao. To se, dakako, da i puno ljepše napisati, bez daljnjega. :)
E, a sad razmisli što ti je zapravo taj pravokutni trokut o kojem se priča. Nacrtaj si sliku! :) (Funkcija je tako zadana da zbilja lako nacrtamo sliku, a može ti dosta pomoći.) E, a mi sad želimo minimizirati umnožak odsječka na [latex]x[/latex]-osi i odsječka na [latex]y[/latex]-osi (to je baš dvostruka površina tog trokuta). Pa dobro, izrazimo duljine tih odsječaka: iznose, ako se ne varam,[latex]x_0+2(x_0-1)^2+(x_0-1)=2x_0^2-2x_0+1[/latex] i [latex]\displaystyle\frac{2x_0^2-2x_0+1}{(x_0-1)^2}[/latex], zar ne? Mislim, ja sam se tu vjerojatno zeznuo, ali ljudi smo. :) Sve u svemu, dakle, želiš minimizirati funkciju [latex]f(x)=\displaystyle\frac{(2x^2-2x+1)^2}{(x-1)^2}[/latex]. No, primijeti da su nam sve ove zagrade tu pozitivne, pa možemo i tražiti minimum od [latex]g(x)=\displaystyle\frac{2x^2-2x+1}{x-1}[/latex]. Dobro, to sad deriviraj i potraži nultočke: to su kandidati za minimum (osim toga, kandidati su i [latex]x\to 1[/latex] i [latex]x\to +\infty[/latex], ali u njima taj umnožak ide u [latex]+\infty[/latex], tako da ništa od toga). U ovom slučaju, taj je samo jedan, čini se (per WolframAlpha), a to bi trebao biti [latex]1+\sqrt{2}/2[/latex], ako ja nisam nešto krivo računao. Vrijednost površine je onda [latex]\displaystyle \frac{f(1+\sqrt{2}/2)}{2}[/latex], a to je neki broj. :P
EDIT: Ispravio jednu relativno veliku računsku grešku. Moje isprike. Nadam se da je sad sve u redu, ali mislim da šanse za to i dalje nisu baš ogromne. :D
Ajde da vidimo: prvo ćemo napisati  u prihvatljivijem obliku: u prihvatljivijem obliku: 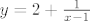 . To nam sad nije problem derivirati: . To nam sad nije problem derivirati: 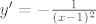 . E, i to je manje-više to: jednadžba tangente u točki . E, i to je manje-više to: jednadžba tangente u točki  je dakle je dakle 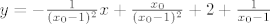 , ako sam ja to dobro izračunao. To se, dakako, da i puno ljepše napisati, bez daljnjega. , ako sam ja to dobro izračunao. To se, dakako, da i puno ljepše napisati, bez daljnjega. 
E, a sad razmisli što ti je zapravo taj pravokutni trokut o kojem se priča. Nacrtaj si sliku!  (Funkcija je tako zadana da zbilja lako nacrtamo sliku, a može ti dosta pomoći.) E, a mi sad želimo minimizirati umnožak odsječka na (Funkcija je tako zadana da zbilja lako nacrtamo sliku, a može ti dosta pomoći.) E, a mi sad želimo minimizirati umnožak odsječka na  -osi i odsječka na -osi i odsječka na  -osi (to je baš dvostruka površina tog trokuta). Pa dobro, izrazimo duljine tih odsječaka: iznose, ako se ne varam, -osi (to je baš dvostruka površina tog trokuta). Pa dobro, izrazimo duljine tih odsječaka: iznose, ako se ne varam,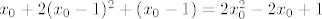 i i 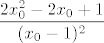 , zar ne? Mislim, ja sam se tu vjerojatno zeznuo, ali ljudi smo. , zar ne? Mislim, ja sam se tu vjerojatno zeznuo, ali ljudi smo.  Sve u svemu, dakle, želiš minimizirati funkciju Sve u svemu, dakle, želiš minimizirati funkciju 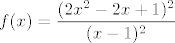 . No, primijeti da su nam sve ove zagrade tu pozitivne, pa možemo i tražiti minimum od . No, primijeti da su nam sve ove zagrade tu pozitivne, pa možemo i tražiti minimum od 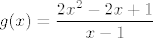 . Dobro, to sad deriviraj i potraži nultočke: to su kandidati za minimum (osim toga, kandidati su i . Dobro, to sad deriviraj i potraži nultočke: to su kandidati za minimum (osim toga, kandidati su i 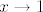 i i 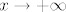 , ali u njima taj umnožak ide u , ali u njima taj umnožak ide u  , tako da ništa od toga). U ovom slučaju, taj je samo jedan, čini se (per WolframAlpha), a to bi trebao biti , tako da ništa od toga). U ovom slučaju, taj je samo jedan, čini se (per WolframAlpha), a to bi trebao biti 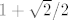 , ako ja nisam nešto krivo računao. Vrijednost površine je onda , ako ja nisam nešto krivo računao. Vrijednost površine je onda 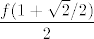 , a to je neki broj. , a to je neki broj. 
EDIT: Ispravio jednu relativno veliku računsku grešku. Moje isprike. Nadam se da je sad sve u redu, ali mislim da šanse za to i dalje nisu baš ogromne. 
Zadnja promjena: mornik; 20:38 pet, 1. 4. 2011; ukupno mijenjano 2 put/a.
|
|
| [Vrh] |
|
moni_poni
Forumaš(ica)

Pridružen/a: 25. 01. 2010. (19:48:19)
Postovi: (49)16
|
|
| [Vrh] |
|
Darija.x
Forumaš(ica)
Pridružen/a: 10. 07. 2008. (18:31:47)
Postovi: (34)16
Lokacija: Velika Gorica
|
|
| [Vrh] |
|
Bruno^_^
Forumaš(ica)

Pridružen/a: 09. 10. 2010. (20:22:27)
Postovi: (1D)16
|
|
| [Vrh] |
|
Darija.x
Forumaš(ica)
Pridružen/a: 10. 07. 2008. (18:31:47)
Postovi: (34)16
Lokacija: Velika Gorica
|
|
| [Vrh] |
|
matijaB
Forumaš(ica)

Pridružen/a: 19. 08. 2010. (09:11:43)
Postovi: (4D)16
|
|
| [Vrh] |
|
mornik
Forumaš(ica)

Pridružen/a: 26. 09. 2009. (06:25:44)
Postovi: (128)16
|
 Postano: 21:51 pet, 1. 4. 2011 Naslov: Postano: 21:51 pet, 1. 4. 2011 Naslov: |
    |
|
|
Hint, jel?
Pa dobro, primijeti (to je i u a) i u b) dijelu) da su nam zapravo jedine sumnjive točke one u kojima [latex]\lfloor x^2\rfloor[/latex] "skače". Naravno, to treba možda malo preciznije argumentirati, ali je intuitivno dosta jasno - van tih točaka, funkcija je dosta bezveze: konstanta pomnožena s nekakvim kvadratom sinusa.
Što se tiče [latex]1.8[/latex], ima smisla, dakle, pronaći najbližu točku prije tog broja u kojem će gornja funkcija "skočiti" i pronaći istu takvu najbližu točku poslije tog broja. To je zapravo to. Bar se nadam. :)
Hint, jel?
Pa dobro, primijeti (to je i u a) i u b) dijelu) da su nam zapravo jedine sumnjive točke one u kojima 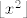 "skače". Naravno, to treba možda malo preciznije argumentirati, ali je intuitivno dosta jasno - van tih točaka, funkcija je dosta bezveze: konstanta pomnožena s nekakvim kvadratom sinusa. "skače". Naravno, to treba možda malo preciznije argumentirati, ali je intuitivno dosta jasno - van tih točaka, funkcija je dosta bezveze: konstanta pomnožena s nekakvim kvadratom sinusa.
Što se tiče 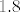 , ima smisla, dakle, pronaći najbližu točku prije tog broja u kojem će gornja funkcija "skočiti" i pronaći istu takvu najbližu točku poslije tog broja. To je zapravo to. Bar se nadam. , ima smisla, dakle, pronaći najbližu točku prije tog broja u kojem će gornja funkcija "skočiti" i pronaći istu takvu najbližu točku poslije tog broja. To je zapravo to. Bar se nadam. 
|
|
| [Vrh] |
|
matijaB
Forumaš(ica)

Pridružen/a: 19. 08. 2010. (09:11:43)
Postovi: (4D)16
|
|
| [Vrh] |
|
Lepi91
Forumaš(ica)


Pridružen/a: 15. 09. 2010. (15:22:23)
Postovi: (C8)16
Spol: 
|
 Postano: 9:57 sub, 2. 4. 2011 Naslov: Postano: 9:57 sub, 2. 4. 2011 Naslov: |
    |
|
|
nisam zao pod koju temu bi ovo stavio,pa evo ovdje:
jel mi može netko reći koja svojstva vrijeda za parne i neparne derivacije parnih i neparnih funkcija;
znači imamo f-parna funkcija,g-neparna funkcija, i sad mene zanima
parna derivacija od f u nuli,neparna derivacija od f u nuli,parna derivacija od g u nuli,neparna derivacija od g u nuli.
nisam zao pod koju temu bi ovo stavio,pa evo ovdje:
jel mi može netko reći koja svojstva vrijeda za parne i neparne derivacije parnih i neparnih funkcija;
znači imamo f-parna funkcija,g-neparna funkcija, i sad mene zanima
parna derivacija od f u nuli,neparna derivacija od f u nuli,parna derivacija od g u nuli,neparna derivacija od g u nuli.
_________________
tko rano rani,malo spava
|
|
| [Vrh] |
|
Bruno^_^
Forumaš(ica)

Pridružen/a: 09. 10. 2010. (20:22:27)
Postovi: (1D)16
|
|
| [Vrh] |
|
piccola
Forumaš(ica)

Pridružen/a: 30. 11. 2009. (15:39:50)
Postovi: (D7)16
|
|
| [Vrh] |
|
Lepi91
Forumaš(ica)


Pridružen/a: 15. 09. 2010. (15:22:23)
Postovi: (C8)16
Spol: 
|
|
| [Vrh] |
|
kikzmyster
Forumaš(ica)

Pridružen/a: 14. 10. 2010. (13:35:08)
Postovi: (72)16
Spol: 
|
|
| [Vrh] |
|
Lepi91
Forumaš(ica)


Pridružen/a: 15. 09. 2010. (15:22:23)
Postovi: (C8)16
Spol: 
|
|
| [Vrh] |
|
rain
Forumaš(ica)

Pridružen/a: 02. 04. 2011. (13:58:42)
Postovi: (13)16
|
|
| [Vrh] |
|
Phoenix
Forumaš(ica)


Pridružen/a: 15. 05. 2010. (18:46:07)
Postovi: (164)16
Sarma: -
|
|
| [Vrh] |
|
|








