| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
anamarie
Forumaš(ica)

Pridružen/a: 07. 09. 2011. (10:59:19)
Postovi: (87)16
Spol: 
|
|
| [Vrh] |
|
jejo
Forumaš(ica)

Pridružen/a: 28. 11. 2006. (19:25:36)
Postovi: (102)16
Spol: 
|
|
| [Vrh] |
|
anamarie
Forumaš(ica)

Pridružen/a: 07. 09. 2011. (10:59:19)
Postovi: (87)16
Spol: 
|
|
| [Vrh] |
|
27re
Forumaš(ica)


Pridružen/a: 06. 10. 2010. (16:07:02)
Postovi: (17)16
|
|
| [Vrh] |
|
mew_17
Forumaš(ica)


Pridružen/a: 12. 07. 2011. (16:38:05)
Postovi: (29)16
Spol: 
|
|
| [Vrh] |
|
slonic~tonic
Forumaš(ica)

Pridružen/a: 26. 10. 2011. (14:16:34)
Postovi: (84)16
Spol: 
|
|
| [Vrh] |
|
Vishykc
Forumaš(ica)


Pridružen/a: 23. 10. 2010. (14:38:08)
Postovi: (6A)16
Spol: 
Lokacija: Zagreb
|
|
| [Vrh] |
|
Zenon
Forumaš(ica)


Pridružen/a: 09. 09. 2011. (19:14:43)
Postovi: (2B1)16
Sarma: -
Lokacija: [tex]\pm\infty[/tex]
|
|
| [Vrh] |
|
anamarie
Forumaš(ica)

Pridružen/a: 07. 09. 2011. (10:59:19)
Postovi: (87)16
Spol: 
|
 Postano: 21:43 sri, 4. 1. 2012 Naslov: Postano: 21:43 sri, 4. 1. 2012 Naslov: |
    |
|
|
[quote="Vishykc"]Ja sam pital prof. i ne znam jel sam dobro skužil, veli isto kad se isprave kolokviji, a usmeni MOŽDA počinju već u petak, 13.1.[/quote]
haha..petak,13..nekima će baš biti zabavno..haha
[size=9][color=#999999]Added after 4 minutes:[/color][/size]
[quote="Zenon"][quote="Vishykc"]a usmeni MOŽDA počinju već u petak, 13.1.[/quote]
Ovo mi je nekako less likely jer to znači da bi onda svi kolokviji koje ćemo mi pisati 9.1. za ta tri-četiri dana trebali biti ispravljeni plus 4. i 5. zadaća koju predajemo na kolokviju. A profesor treba imati ako ništa drugo rezultate drugog kolokvija da zaključi ocjenu :P
Ne kažem da nije moguće, nego mi je baš zvuči nekako kao da je mala vjerojatnost da to bude. Iskreno, nadam se da neće :P[/quote]
analizu inače jako brzo ispravljaju..pa je nažalost moguće..
| Vishykc (napisa): | | Ja sam pital prof. i ne znam jel sam dobro skužil, veli isto kad se isprave kolokviji, a usmeni MOŽDA počinju već u petak, 13.1. |
haha..petak,13..nekima će baš biti zabavno..haha
Added after 4 minutes:
| Zenon (napisa): | | Vishykc (napisa): | | a usmeni MOŽDA počinju već u petak, 13.1. |
Ovo mi je nekako less likely jer to znači da bi onda svi kolokviji koje ćemo mi pisati 9.1. za ta tri-četiri dana trebali biti ispravljeni plus 4. i 5. zadaća koju predajemo na kolokviju. A profesor treba imati ako ništa drugo rezultate drugog kolokvija da zaključi ocjenu 
Ne kažem da nije moguće, nego mi je baš zvuči nekako kao da je mala vjerojatnost da to bude. Iskreno, nadam se da neće  |
analizu inače jako brzo ispravljaju..pa je nažalost moguće..
|
|
| [Vrh] |
|
kiara
Forumaš(ica)

Pridružen/a: 15. 11. 2011. (23:22:57)
Postovi: (55)16
|
|
| [Vrh] |
|
Hubert Cumberdale
Forumaš(ica)


Pridružen/a: 10. 11. 2011. (11:43:04)
Postovi: (24)16
Spol: 
|
|
| [Vrh] |
|
satja
Forumaš(ica)

Pridružen/a: 16. 05. 2010. (10:44:17)
Postovi: (F1)16
|
|
| [Vrh] |
|
Hubert Cumberdale
Forumaš(ica)


Pridružen/a: 10. 11. 2011. (11:43:04)
Postovi: (24)16
Spol: 
|
 Postano: 13:19 čet, 5. 1. 2012 Naslov: Postano: 13:19 čet, 5. 1. 2012 Naslov: |
    |
|
|
[quote="satja"][quote="Hubert Cumberdale"]Hej, imam pitanje. Učim za usmeni i prof nam je zadao za dz dokazati da je f(x)=x^n strogo rastuća, s napomenom da dakle treba pokazati da za x1<x2 slijedi x2^n - x1^n > 0. Uz to je i rekao da je to često pitanje na usmenom pa zato gnjavim :D[/quote]
[tex]f(x)=x^2[/tex] nije strogo rastuća na [tex]\mathbb{R}[/tex]. Vjerojatno si zaboravio neki uvjet: možda se gleda na [tex]\mathbb{R}^+[/tex] ili je [tex]n[/tex] neparan.[/quote]
Ma naravno, da, zaboravila sam napisati, traži se dokaz za n neparan. Sry.
E i još jedno, treba dokazati ln(a^x)=x*ln a, piše da je dokaz sličan ovome dokazu:
e^x=a, e^y=b, e^(x+y)=a*b
=> ln(a*b) = f^(-1) (a*b) = x+y = f^(-1) (a) + f^(-1) (b) = lna + lnb
Hvala što će se (ako će se) nekome dati gnjaviti s ovime :D
| satja (napisa): | | Hubert Cumberdale (napisa): | Hej, imam pitanje. Učim za usmeni i prof nam je zadao za dz dokazati da je f(x)=x^n strogo rastuća, s napomenom da dakle treba pokazati da za x1<x2 slijedi x2^n - x1^n > 0. Uz to je i rekao da je to često pitanje na usmenom pa zato gnjavim  |
[tex]f(x)=x^2[/tex] nije strogo rastuća na [tex]\mathbb{R}[/tex]. Vjerojatno si zaboravio neki uvjet: možda se gleda na [tex]\mathbb{R}^+[/tex] ili je [tex]n[/tex] neparan. |
Ma naravno, da, zaboravila sam napisati, traži se dokaz za n neparan. Sry.
E i još jedno, treba dokazati ln(a^x)=x*ln a, piše da je dokaz sličan ovome dokazu:
e^x=a, e^y=b, e^(x+y)=a*b
⇒ ln(a*b) = f^(-1) (a*b) = x+y = f^(-1) (a) + f^(-1) (b) = lna + lnb
Hvala što će se (ako će se) nekome dati gnjaviti s ovime 
|
|
| [Vrh] |
|
satja
Forumaš(ica)

Pridružen/a: 16. 05. 2010. (10:44:17)
Postovi: (F1)16
|
 Postano: 13:28 čet, 5. 1. 2012 Naslov: Postano: 13:28 čet, 5. 1. 2012 Naslov: |
    |
|
|
[quote="Hubert Cumberdale"][quote="satja"][quote="Hubert Cumberdale"]Hej, imam pitanje. Učim za usmeni i prof nam je zadao za dz dokazati da je f(x)=x^n strogo rastuća, s napomenom da dakle treba pokazati da za x1<x2 slijedi x2^n - x1^n > 0. Uz to je i rekao da je to često pitanje na usmenom pa zato gnjavim :D[/quote]
[tex]f(x)=x^2[/tex] nije strogo rastuća na [tex]\mathbb{R}[/tex]. Vjerojatno si zaboravio neki uvjet: možda se gleda na [tex]\mathbb{R}^+[/tex] ili je [tex]n[/tex] neparan.[/quote]
Ma naravno, da, zaboravila sam napisati, traži se dokaz za n neparan. Sry.[/quote]
Eksponent je neparan, pa iskoristi formulu [dtex]a^{2k+1}-b^{2k+1}=(a-b)(a^{2k}+a^{2k-1}b+a^{2k-2}b^2+\ldots+ab^{2k-1}+b^{2k}).[/dtex] Za [tex]a>b[/tex], prva zagrada je očito pozitivna. Ako su [tex]a, b[/tex] istog predznaka, onda je i druga zagrada pozitivna jer su svi pribrojnici pozitivni. Ako su [tex]a, b[/tex] različitog predznaka, onda je tvrdnja jasna jer je tada [tex]a^{2n+1}[/tex] pozitivan dok je [tex]b^{2n+1}[/tex] negativan.
| Hubert Cumberdale (napisa): | | satja (napisa): | | Hubert Cumberdale (napisa): | Hej, imam pitanje. Učim za usmeni i prof nam je zadao za dz dokazati da je f(x)=x^n strogo rastuća, s napomenom da dakle treba pokazati da za x1<x2 slijedi x2^n - x1^n > 0. Uz to je i rekao da je to često pitanje na usmenom pa zato gnjavim  |
[tex]f(x)=x^2[/tex] nije strogo rastuća na [tex]\mathbb{R}[/tex]. Vjerojatno si zaboravio neki uvjet: možda se gleda na [tex]\mathbb{R}^+[/tex] ili je [tex]n[/tex] neparan. |
Ma naravno, da, zaboravila sam napisati, traži se dokaz za n neparan. Sry. |
Eksponent je neparan, pa iskoristi formulu [dtex]a^{2k+1}-b^{2k+1}=(a-b)(a^{2k}+a^{2k-1}b+a^{2k-2}b^2+\ldots+ab^{2k-1}+b^{2k}).[/dtex] Za [tex]a>b[/tex], prva zagrada je očito pozitivna. Ako su [tex]a, b[/tex] istog predznaka, onda je i druga zagrada pozitivna jer su svi pribrojnici pozitivni. Ako su [tex]a, b[/tex] različitog predznaka, onda je tvrdnja jasna jer je tada [tex]a^{2n+1}[/tex] pozitivan dok je [tex]b^{2n+1}[/tex] negativan.
|
|
| [Vrh] |
|
bloo
Forumaš(ica)

Pridružen/a: 06. 11. 2011. (12:43:21)
Postovi: (2)16
|
|
| [Vrh] |
|
student_92
Forumaš(ica)

Pridružen/a: 17. 09. 2011. (16:31:46)
Postovi: (B9)16
|
|
| [Vrh] |
|
Orah
Forumaš(ica)

Pridružen/a: 21. 01. 2012. (13:04:59)
Postovi: (A)16
|
|
| [Vrh] |
|
anamarie
Forumaš(ica)

Pridružen/a: 07. 09. 2011. (10:59:19)
Postovi: (87)16
Spol: 
|
|
| [Vrh] |
|
weeh
Forumaš(ica)
Pridružen/a: 29. 10. 2008. (00:00:53)
Postovi: (32)16
Spol: 
Lokacija: Zagreb
|
 Postano: 20:49 pon, 30. 1. 2012 Naslov: Postano: 20:49 pon, 30. 1. 2012 Naslov: |
    |
|
|
[quote="Hubert Cumberdale"][quote="satja"][quote="Hubert Cumberdale"]Hej, imam pitanje. Učim za usmeni i prof nam je zadao za dz dokazati da je f(x)=x^n strogo rastuća, s napomenom da dakle treba pokazati da za x1<x2 slijedi x2^n - x1^n > 0. Uz to je i rekao da je to često pitanje na usmenom pa zato gnjavim :D[/quote]
[tex]f(x)=x^2[/tex] nije strogo rastuća na [tex]\mathbb{R}[/tex]. Vjerojatno si zaboravio neki uvjet: možda se gleda na [tex]\mathbb{R}^+[/tex] ili je [tex]n[/tex] neparan.[/quote]
Ma naravno, da, zaboravila sam napisati, traži se dokaz za n neparan. Sry.
E i još jedno, treba dokazati ln(a^x)=x*ln a, piše da je dokaz sličan ovome dokazu:
e^x=a, e^y=b, e^(x+y)=a*b
=> ln(a*b) = f^(-1) (a*b) = x+y = f^(-1) (a) + f^(-1) (b) = lna + lnb
Hvala što će se (ako će se) nekome dati gnjaviti s ovime :D[/quote]
Ne znam koliko ste došli s usmenima i dal će vam još koristiti, ali eto:
[latex]\ln(a^b)=b\ln(a)[/latex]napadnemo sa[latex]x \mapsto e^x[/latex] dobivamo [latex]a^b=e^{b\ln(a))=(e^{ln(a)})^b=a^b[/latex], pa to vrijedi za sve a i b dobro definirane.
| Hubert Cumberdale (napisa): | | satja (napisa): | | Hubert Cumberdale (napisa): | Hej, imam pitanje. Učim za usmeni i prof nam je zadao za dz dokazati da je f(x)=x^n strogo rastuća, s napomenom da dakle treba pokazati da za x1<x2 slijedi x2^n - x1^n > 0. Uz to je i rekao da je to često pitanje na usmenom pa zato gnjavim  |
[tex]f(x)=x^2[/tex] nije strogo rastuća na [tex]\mathbb{R}[/tex]. Vjerojatno si zaboravio neki uvjet: možda se gleda na [tex]\mathbb{R}^+[/tex] ili je [tex]n[/tex] neparan. |
Ma naravno, da, zaboravila sam napisati, traži se dokaz za n neparan. Sry.
E i još jedno, treba dokazati ln(a^x)=x*ln a, piše da je dokaz sličan ovome dokazu:
e^x=a, e^y=b, e^(x+y)=a*b
⇒ ln(a*b) = f^(-1) (a*b) = x+y = f^(-1) (a) + f^(-1) (b) = lna + lnb
Hvala što će se (ako će se) nekome dati gnjaviti s ovime  |
Ne znam koliko ste došli s usmenima i dal će vam još koristiti, ali eto:
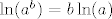 napadnemo sa napadnemo sa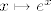 dobivamo dobivamo 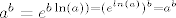 , pa to vrijedi za sve a i b dobro definirane. , pa to vrijedi za sve a i b dobro definirane.
|
|
| [Vrh] |
|
Orah
Forumaš(ica)

Pridružen/a: 21. 01. 2012. (13:04:59)
Postovi: (A)16
|
 Postano: 0:27 uto, 31. 1. 2012 Naslov: Postano: 0:27 uto, 31. 1. 2012 Naslov: |
    |
|
|
[quote="anamarie"][quote="Orah"]Kad će onda biti zadnji rokovi za usmeni kod prof. Šikića (usmeni popravnog i popravni usmenog)? Jel možda pišu negdje na faksu? Zna li se barem okvirno kad će biti?[/quote]
znam da su popravni usmenog danas počeli,profesor je njima odmah rekao kad će odgovarati,a za vas sa popravnog ne znam[/quote]
Ako bi netko od kolega slučajno saznao te termine, bio bih im neizmjerno zahvalan ako bi ih ovdje postali. Znam da smo najmanje samo dvoje s popravnoga, ali i mi zaslužujemo znati, ne? :P
| anamarie (napisa): | | Orah (napisa): | | Kad će onda biti zadnji rokovi za usmeni kod prof. Šikića (usmeni popravnog i popravni usmenog)? Jel možda pišu negdje na faksu? Zna li se barem okvirno kad će biti? |
znam da su popravni usmenog danas počeli,profesor je njima odmah rekao kad će odgovarati,a za vas sa popravnog ne znam |
Ako bi netko od kolega slučajno saznao te termine, bio bih im neizmjerno zahvalan ako bi ih ovdje postali. Znam da smo najmanje samo dvoje s popravnoga, ali i mi zaslužujemo znati, ne? 
|
|
| [Vrh] |
|
|















