| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
aso2
Forumaš(ica)

Pridružen/a: 08. 01. 2010. (17:53:36)
Postovi: (9)16
|
|
| [Vrh] |
|
vsego
Site Admin


Pridružen/a: 06. 10. 2002. (22:07:09)
Postovi: (3562)16
Spol: 
Lokacija: /sbin/init
|
 Postano: 21:55 sri, 8. 2. 2012 Naslov: Postano: 21:55 sri, 8. 2. 2012 Naslov: |
    |
|
|
Nacrtaj kruznicu, trokut i spojnice srediste kruznice [i]T[/i] s vrhovima trokuta. Dobit ces tri jednakokracna trokuta s krakovima [i]r[/i] i bazama [i]a[/i], [i]b[/i], odnosno [i]c[/i] (njega trazis). Upetljas [url=http://matematika-gradim1.blogspot.com/2010/01/sinusov-i-kosinusov-poucak.html]poucak o kosinusima[/url] i nadjes kuteve uz [i]T[/i] u dva trokuta. Onda znas i treci kut, pa opet upotrijebis isti poucak i nadjes trecu stranicu trokuta. Za ostale kuteve je lako (isti poucak, samo gledas pocetni trokut umjesto ova tri "mala").
Nacrtaj kruznicu, trokut i spojnice srediste kruznice T s vrhovima trokuta. Dobit ces tri jednakokracna trokuta s krakovima r i bazama a, b, odnosno c (njega trazis). Upetljas poucak o kosinusima i nadjes kuteve uz T u dva trokuta. Onda znas i treci kut, pa opet upotrijebis isti poucak i nadjes trecu stranicu trokuta. Za ostale kuteve je lako (isti poucak, samo gledas pocetni trokut umjesto ova tri "mala").
_________________ U pravilu ignoriram pitanja u krivim topicima i kodove koji nisu u [code]...[/code] blokovima.
Takodjer, OBJASNITE sto vas muci! "Sto mi je krivo?", bez opisa u cemu je problem, rijetko ce zadobiti moju paznju.  |
|
| [Vrh] |
|
kikzmyster
Forumaš(ica)

Pridružen/a: 14. 10. 2010. (13:35:08)
Postovi: (72)16
Spol: 
|
 Postano: 21:59 sri, 8. 2. 2012 Naslov: Postano: 21:59 sri, 8. 2. 2012 Naslov: |
    |
|
|
Oznacimo sa a,b,c stranice trokuta, a= 5 cm, b = 5.8 cm, i sa [latex]\alpha , \beta, \gamma[/latex] odgovarajuce kuteve. Oznacimo R = 3.6 cm.
Znamo da je polumjer kruznice opisana trokutu [latex]R=\frac{abc}{4P}[/latex], gdje je P povrsina trokuta. Povrsinu racunamo pomocu Heronove formule, [latex] P = \sqrt{s(s-a)(s-b)(s-c)} [/latex], gdje je [latex] s= \frac{a+b+c}{2} [/latex].
Dakle imamo sve skupa [latex]R=\frac{abc}{4\sqrt{s(s-a)(s-b)(s-c)}}[/latex]. Uvrstimo sto znamo, i dobit cemo jednadzbu za c. Bit ce jednadzba 4-tog stupnja, ali oblika Ac^4 + Bc^2 + C = 0. pa rjesavas za c^2. Tako znamo a,b,c, pa kuteve odredujemo pomocu sinusovog poucka. [latex] \frac{a}{sin \alpha } = \frac{b}{sin \beta } = \frac{c}{sin \gamma } = 2R [/latex]
EDIT: sad vidio da nisam prvi. ovo gore je puno jednostavnije..
Oznacimo sa a,b,c stranice trokuta, a= 5 cm, b = 5.8 cm, i sa 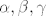 odgovarajuce kuteve. Oznacimo R = 3.6 cm. odgovarajuce kuteve. Oznacimo R = 3.6 cm.
Znamo da je polumjer kruznice opisana trokutu 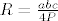 , gdje je P povrsina trokuta. Povrsinu racunamo pomocu Heronove formule, , gdje je P povrsina trokuta. Povrsinu racunamo pomocu Heronove formule, 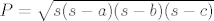 , gdje je , gdje je 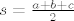 . .
Dakle imamo sve skupa 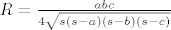 . Uvrstimo sto znamo, i dobit cemo jednadzbu za c. Bit ce jednadzba 4-tog stupnja, ali oblika Ac^4 + Bc^2 + C = 0. pa rjesavas za c^2. Tako znamo a,b,c, pa kuteve odredujemo pomocu sinusovog poucka. . Uvrstimo sto znamo, i dobit cemo jednadzbu za c. Bit ce jednadzba 4-tog stupnja, ali oblika Ac^4 + Bc^2 + C = 0. pa rjesavas za c^2. Tako znamo a,b,c, pa kuteve odredujemo pomocu sinusovog poucka. 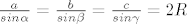
EDIT: sad vidio da nisam prvi. ovo gore je puno jednostavnije..
|
|
| [Vrh] |
|
krki
Forumaš(ica)

Pridružen/a: 06. 07. 2011. (20:30:12)
Postovi: (2E)16
|
|
| [Vrh] |
|
aso2
Forumaš(ica)

Pridružen/a: 08. 01. 2010. (17:53:36)
Postovi: (9)16
|
|
| [Vrh] |
|
|





