| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
goranm
Forumaš(ica)


Pridružen/a: 12. 11. 2002. (20:09:12)
Postovi: (906)16
Spol: 
|
 Postano: 17:13 sri, 18. 4. 2012 Naslov: Postano: 17:13 sri, 18. 4. 2012 Naslov: |
    |
|
|
[quote="ceps"]Zato jer je podgrupa od G (koja je Abelova).[/quote]
Grupa G ne mora biti abelova. Treba iskoristiti da je G/G1 abelova i da je G1<H1. Dakle, [tex]xyH_1=yxH_1 (\iff xyx^{-1}y^{-1}\in H_1)[/tex] vrijedi za sve x,y iz H jer vrijedi [tex]xyG_1=yxG_1[/tex], odnosno [tex]xyx^{-1}y^{-1}\in G_1<H_1[/tex] za sve x,y iz G, pa onda posebno i za sve x,y iz H.
| ceps (napisa): | | Zato jer je podgrupa od G (koja je Abelova). |
Grupa G ne mora biti abelova. Treba iskoristiti da je G/G1 abelova i da je G1<H1. Dakle, [tex]xyH_1=yxH_1 (\iff xyx^{-1}y^{-1}\in H_1)[/tex] vrijedi za sve x,y iz H jer vrijedi [tex]xyG_1=yxG_1[/tex], odnosno [tex]xyx^{-1}y^{-1}\in G_1<H_1[/tex] za sve x,y iz G, pa onda posebno i za sve x,y iz H.
_________________
The Dude Abides
Zadnja promjena: goranm; 17:35 sri, 18. 4. 2012; ukupno mijenjano 2 put/a.
|
|
| [Vrh] |
|
ceps
Forumaš(ica)

Pridružen/a: 08. 10. 2010. (13:03:07)
Postovi: (13A)16
|
|
| [Vrh] |
|
kkarlo
Forumaš(ica)

Pridružen/a: 19. 05. 2010. (08:43:59)
Postovi: (1B2)16
Spol: 
|
 Postano: 17:56 sri, 18. 4. 2012 Naslov: Postano: 17:56 sri, 18. 4. 2012 Naslov: |
    |
|
|
Evo nečega što se čini jednostavno ali opet...
Kako se određuje Int(Z9)?
Znam da je to kao skup svih Ig-ova gdje je Ig(x)=gxg^(-1) za svaki g iz Z9, pri cemu je x isto iz Z9...valjda?
I sad posto su u Z9={0,1,2,3,4,5,6,7,8},
koji bi bili Ig-ovi?
jel ih onda imamo 9?
:?
Evo nečega što se čini jednostavno ali opet...
Kako se određuje Int(Z9)?
Znam da je to kao skup svih Ig-ova gdje je Ig(x)=gxg^(-1) za svaki g iz Z9, pri cemu je x isto iz Z9...valjda?
I sad posto su u Z9={0,1,2,3,4,5,6,7,8},
koji bi bili Ig-ovi?
jel ih onda imamo 9?

|
|
| [Vrh] |
|
ceps
Forumaš(ica)

Pridružen/a: 08. 10. 2010. (13:03:07)
Postovi: (13A)16
|
|
| [Vrh] |
|
kkarlo
Forumaš(ica)

Pridružen/a: 19. 05. 2010. (08:43:59)
Postovi: (1B2)16
Spol: 
|
 Postano: 18:14 sri, 18. 4. 2012 Naslov: Postano: 18:14 sri, 18. 4. 2012 Naslov: |
    |
|
|
[quote="ceps"][latex]\mathbb{Z}_9[/latex] je komutativna grupa, zar ne?
Općenito, ako je G komutativna grupa:
[latex]I_g(x) = gxg^{-1} = gg^{-1}x = x, \hspace{3mm} \forall g,x \in G[/latex]
Što onda možeš reći o [latex]I_g[/latex]-ovima?
Ili probaj neki konkretan primjer ako ti je ovo preapstraktno, uzmi recimo [latex]I_3[/latex]. Kako on djeluje na elemente [latex]\mathbb{Z}_9[/latex]?[/quote]
Da, pošto je Z9 komutativna onda to je tak kak si napisao... Ali ovo pitanje koje si ti meni postavio to je ono što me ustvari muči...
Pretpostavljam da pošto je riječ o Z da se gleda operacija zbrajanja, gdje je neutralni element 0. pa bi onda inverz od 3 bio 6, ako sam dobro shvatio...
I jasno je meni sad da je 3+x+6=x, ali ak možeš neki drugi primjer rješit di to nije tako jednostavno, zapravo samo da pokažeš na nekomutativnoj grupi...
I naravno da me ispraviš ako je ovo gore krivo, jer nisam siguran ni u to...
EDIT:
Baš gledam uvijek se koristi kod Z-a, tako da je uvijek komutativna...Ali opet što je onda I3 u tom primjeru koji smo naveli gore(Z9) jel to onda cijeli Z9, tj za bilo koji g, Ig je identiteta?
| ceps (napisa): |  je komutativna grupa, zar ne? je komutativna grupa, zar ne?
Općenito, ako je G komutativna grupa:
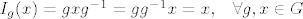
Što onda možeš reći o 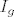 -ovima? -ovima?
Ili probaj neki konkretan primjer ako ti je ovo preapstraktno, uzmi recimo 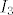 . Kako on djeluje na elemente . Kako on djeluje na elemente  ? ? |
Da, pošto je Z9 komutativna onda to je tak kak si napisao... Ali ovo pitanje koje si ti meni postavio to je ono što me ustvari muči...
Pretpostavljam da pošto je riječ o Z da se gleda operacija zbrajanja, gdje je neutralni element 0. pa bi onda inverz od 3 bio 6, ako sam dobro shvatio...
I jasno je meni sad da je 3+x+6=x, ali ak možeš neki drugi primjer rješit di to nije tako jednostavno, zapravo samo da pokažeš na nekomutativnoj grupi...
I naravno da me ispraviš ako je ovo gore krivo, jer nisam siguran ni u to...
EDIT:
Baš gledam uvijek se koristi kod Z-a, tako da je uvijek komutativna...Ali opet što je onda I3 u tom primjeru koji smo naveli gore(Z9) jel to onda cijeli Z9, tj za bilo koji g, Ig je identiteta?
|
|
| [Vrh] |
|
kikzmyster
Forumaš(ica)

Pridružen/a: 14. 10. 2010. (13:35:08)
Postovi: (72)16
Spol: 
|
 Postano: 18:22 sri, 18. 4. 2012 Naslov: Postano: 18:22 sri, 18. 4. 2012 Naslov: |
    |
|
|
pa, jer je Z9 komutativna, slijedi da je identiteta jedina funkcija u Int(Z9), kako je ceps dao naslutit. Kad promatramo Int od neke nekomutativne grupe, to je druga prica
EDIT: [tex] Int(A)[/tex] je skup svih [tex]I_g[/tex]-ova, dakle skup svih unutrasnjih automorfizama neke grupe. Jer je Z9 komutativna dobijemo da je [tex]I_i = id, \ \forall i \in \{0,1,2,\ldots,8\}[/tex], dakle [tex]Int(\mathbb{Z}_9) = \{id\} [/tex]
pa, jer je Z9 komutativna, slijedi da je identiteta jedina funkcija u Int(Z9), kako je ceps dao naslutit. Kad promatramo Int od neke nekomutativne grupe, to je druga prica
EDIT: [tex] Int(A)[/tex] je skup svih [tex]I_g[/tex]-ova, dakle skup svih unutrasnjih automorfizama neke grupe. Jer je Z9 komutativna dobijemo da je [tex]I_i = id, \ \forall i \in \{0,1,2,\ldots,8\}[/tex], dakle [tex]Int(\mathbb{Z}_9) = \{id\} [/tex]
Zadnja promjena: kikzmyster; 18:26 sri, 18. 4. 2012; ukupno mijenjano 1 put.
|
|
| [Vrh] |
|
ceps
Forumaš(ica)

Pridružen/a: 08. 10. 2010. (13:03:07)
Postovi: (13A)16
|
|
| [Vrh] |
|
kkarlo
Forumaš(ica)

Pridružen/a: 19. 05. 2010. (08:43:59)
Postovi: (1B2)16
Spol: 
|
 Postano: 18:37 sri, 18. 4. 2012 Naslov: Postano: 18:37 sri, 18. 4. 2012 Naslov: |
    |
|
|
[quote="ceps"]Ovdje bi se trebalo zaključiti da je [latex]Int(\mathbb{Z}_9) = \{id\}[/latex], samo da to bude jasno.
A ne znam kakav bi ti primjer želio...
[b]Ako ti nešto nije jasno, slobodno pitaj.[/b] :)[/quote]
Jasno mi je...ili barem jasnije nego li mi je prije bilo...
a sad dalje:
http://web.math.pmf.unizg.hr/nastava/alg/2008-09/kolokvij200409.pdf
To je 3 zadatak pod a)
Za Aut(Z9) mi je jasno, i znam ih odredit, i onda bi valjda odgovor bio da to jesu cikličke grupe pošto za svaki Aut(Z9) postoji generator kojim se može generirati cijeli Z9, a i kod Int(Z9) imamo opet Z9 koji je ciklička grupa...Pa onda jesu.
Ali pod b.) mi nije jasan. Zapravo, da bi bolje objasnio svoje neznanje, nije mi jasna upotreba direktne sume produkta.
Što bi to bilo Z(direktna suma produkta)Z?
Kada bih to znao možda bi znao i odredit Int i Aut od toga...
I odmah da kažem hvala na pomoći...(a sad onda želim pitat sve što mi nije jasno-ali samo iz algebarskih :lol: )
:D
| ceps (napisa): | Ovdje bi se trebalo zaključiti da je 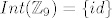 , samo da to bude jasno. , samo da to bude jasno.
A ne znam kakav bi ti primjer želio...
Ako ti nešto nije jasno, slobodno pitaj.  |
Jasno mi je...ili barem jasnije nego li mi je prije bilo...
a sad dalje:
http://web.math.pmf.unizg.hr/nastava/alg/2008-09/kolokvij200409.pdf
To je 3 zadatak pod a)
Za Aut(Z9) mi je jasno, i znam ih odredit, i onda bi valjda odgovor bio da to jesu cikličke grupe pošto za svaki Aut(Z9) postoji generator kojim se može generirati cijeli Z9, a i kod Int(Z9) imamo opet Z9 koji je ciklička grupa...Pa onda jesu.
Ali pod b.) mi nije jasan. Zapravo, da bi bolje objasnio svoje neznanje, nije mi jasna upotreba direktne sume produkta.
Što bi to bilo Z(direktna suma produkta)Z?
Kada bih to znao možda bi znao i odredit Int i Aut od toga...
I odmah da kažem hvala na pomoći...(a sad onda želim pitat sve što mi nije jasno-ali samo iz algebarskih  ) )

|
|
| [Vrh] |
|
goranm
Forumaš(ica)


Pridružen/a: 12. 11. 2002. (20:09:12)
Postovi: (906)16
Spol: 
|
 Postano: 19:14 sri, 18. 4. 2012 Naslov: Postano: 19:14 sri, 18. 4. 2012 Naslov: |
    |
|
|
[quote="kkarlo"]Pretpostavljam da pošto je riječ o Z da se gleda operacija zbrajanja, gdje je neutralni element 0. pa bi onda inverz od 3 bio 6, ako sam dobro shvatio...[/quote]
Mala napomena: nije riječ o Z, riječ je o Z9, tj. o kvocijentnoj grupi Z/9Z. Iako grupe Z i Z9 imaju mnoge sličnosti, ne preporučam razmišljati o Z9 kao o podskupu od Z.
[quote]ali ak možeš neki drugi primjer rješit di to nije tako jednostavno, zapravo samo da pokažeš na nekomutativnoj grupi...[/quote]
Neka je G grupa i neka je [tex]\varphi\colon G\to \text{Inn}(G)[/tex] funkcija definirana s [tex]\varphi(g)=I_g[/tex], gdje je [tex]I_g\colon G\to G[/tex] unutrašnji automorfizam grupe G određen elementom g, tj. [tex]I_g(x)=gxg^{-1}[/tex].
Koristeći elementarne činjenice o kompoziciji bijekcija pokazuje se da je [tex]\varphi[/tex] homomorfizam grupa. Štoviše, [tex]\varphi[/tex] je i epimorfizam pa prema 1. teoremu o izomorfizmu vrijedi [tex]G/\ker{\varphi}\cong \text{Inn}(G).[/tex]
Koristeći da je [tex]I_e\colon G\to G, I_e(x)=exe^{-1}=x[/tex] identiteta u grupi Inn(G), pokazuje se da je [tex]a\in\ker\varphi\iff a\in Z(G)[/tex], pri čemu je Z(G) centar grupe G.
Prema tome, vrijedi [tex]\text{Inn}(G)\cong G/Z(G)[/tex].
To vrijedi za sve grupe, bile one konačne, beskonačne, abelove ili neabelove. U slučaju abelovih grupa (kao što je npr. Z9) uvijek vrijedi Z(G)=G pa je Inn(G) izomorfno s G/Z(G) što je jednako G/G, a to je izomorfno s trivijalnom grupom <0> pa u slučaju abelovih grupa vrijedi [tex]\text{Inn}(G)\cong\left\langle 0 \right\rangle[/tex] kao što su kolege i pokazali ranije direktnim računom.
[size=9][color=#999999]Added after 27 minutes:[/color][/size]
[quote="kkarlo"]Za Aut(Z9) mi je jasno, i znam ih odredit, i onda bi valjda odgovor bio da to jesu cikličke grupe pošto za svaki Aut(Z9) postoji generator kojim se može generirati cijeli Z9, a i kod Int(Z9) imamo opet Z9 koji je ciklička grupa...Pa onda jesu.[/quote]
Nisu zbog toga cikličke. Grupa Aut(Z9) će biti ciklička ako potoji element u Aut(Z9) koji generira čitav Aut(Z9), a ne Z9. Koji su sve izomorfizmi u toj grupi? Možeš li s nekim izomorfizmom generirati čitav Aut(Z9)?
Što se tiče cikličnosti od Inn(Z9), može se reći da je ona ciklička jer je Z9 ciklička, [b]ali samo ako to argumentiraš rezultatom koji sam napisao u prethodnom postu[/b], tj. da je [tex]\mathbb{Z}_9/Z(\mathbb{Z}_9)\cong\text{Inn}(\mathbb{Z}_9) [/tex], jer svaka ciklička grupa G je abelova pa joj je centar jednak čitavoj grupi G pa je onda Inn(G) trivijalna grupa koja je ciklička jer ju generira identiteta.
Možeš koristiti i jednostavniji argument. ceps i kikzmyster su s nešto manje mašinerije pokazali da je Inn(Z9) zapravo trivijalna grupa, pa je zbog toga ta grupa ciklička.
[quote]Ali pod b.) mi nije jasan. Zapravo, da bi bolje objasnio svoje neznanje, nije mi jasna upotreba direktne sume produkta.
Što bi to bilo Z(direktna suma produkta)Z?[/quote]
Termin direktna suma produkta nije dobar, kaže se samo direktna suma. Ne trebaš previše razbijati glavu oko toga - kada je konačno mnogo sumanada, onda je direktna suma ekvivalentna direktnom produktu, a koristimo oznaku [latex]\oplus[/latex] umjesto X jer radimo s abelovim grupama.
[quote]Kada bih to znao možda bi znao i odredit Int i Aut od toga...
I odmah da kažem hvala na pomoći...(a sad onda želim pitat sve što mi nije jasno-ali samo iz algebarskih :lol: )
:D[/quote]
Dakle, [tex]\mathbb{Z}\oplus \mathbb{Z}=\left\{(a,b)|a\in\mathbb{Z},b\in\mathbb{Z}\right\}[/tex] i to je grupa s obzirom na operaciju zbrajanja po koordinatama, tj. (a,b)+(c,d)=(a+c,b+d). Neutralni element je (0,0), a inverz od (a,b) je (-a,-b).
| kkarlo (napisa): | | Pretpostavljam da pošto je riječ o Z da se gleda operacija zbrajanja, gdje je neutralni element 0. pa bi onda inverz od 3 bio 6, ako sam dobro shvatio... |
Mala napomena: nije riječ o Z, riječ je o Z9, tj. o kvocijentnoj grupi Z/9Z. Iako grupe Z i Z9 imaju mnoge sličnosti, ne preporučam razmišljati o Z9 kao o podskupu od Z.
| Citat: | | ali ak možeš neki drugi primjer rješit di to nije tako jednostavno, zapravo samo da pokažeš na nekomutativnoj grupi... |
Neka je G grupa i neka je [tex]\varphi\colon G\to \text{Inn}(G)[/tex] funkcija definirana s [tex]\varphi(g)=I_g[/tex], gdje je [tex]I_g\colon G\to G[/tex] unutrašnji automorfizam grupe G određen elementom g, tj. [tex]I_g(x)=gxg^{-1}[/tex].
Koristeći elementarne činjenice o kompoziciji bijekcija pokazuje se da je [tex]\varphi[/tex] homomorfizam grupa. Štoviše, [tex]\varphi[/tex] je i epimorfizam pa prema 1. teoremu o izomorfizmu vrijedi [tex]G/\ker{\varphi}\cong \text{Inn}(G).[/tex]
Koristeći da je [tex]I_e\colon G\to G, I_e(x)=exe^{-1}=x[/tex] identiteta u grupi Inn(G), pokazuje se da je [tex]a\in\ker\varphi\iff a\in Z(G)[/tex], pri čemu je Z(G) centar grupe G.
Prema tome, vrijedi [tex]\text{Inn}(G)\cong G/Z(G)[/tex].
To vrijedi za sve grupe, bile one konačne, beskonačne, abelove ili neabelove. U slučaju abelovih grupa (kao što je npr. Z9) uvijek vrijedi Z(G)=G pa je Inn(G) izomorfno s G/Z(G) što je jednako G/G, a to je izomorfno s trivijalnom grupom <0> pa u slučaju abelovih grupa vrijedi [tex]\text{Inn}(G)\cong\left\langle 0 \right\rangle[/tex] kao što su kolege i pokazali ranije direktnim računom.
Added after 27 minutes:
| kkarlo (napisa): | | Za Aut(Z9) mi je jasno, i znam ih odredit, i onda bi valjda odgovor bio da to jesu cikličke grupe pošto za svaki Aut(Z9) postoji generator kojim se može generirati cijeli Z9, a i kod Int(Z9) imamo opet Z9 koji je ciklička grupa...Pa onda jesu. |
Nisu zbog toga cikličke. Grupa Aut(Z9) će biti ciklička ako potoji element u Aut(Z9) koji generira čitav Aut(Z9), a ne Z9. Koji su sve izomorfizmi u toj grupi? Možeš li s nekim izomorfizmom generirati čitav Aut(Z9)?
Što se tiče cikličnosti od Inn(Z9), može se reći da je ona ciklička jer je Z9 ciklička, ali samo ako to argumentiraš rezultatom koji sam napisao u prethodnom postu, tj. da je [tex]\mathbb{Z}_9/Z(\mathbb{Z}_9)\cong\text{Inn}(\mathbb{Z}_9) [/tex], jer svaka ciklička grupa G je abelova pa joj je centar jednak čitavoj grupi G pa je onda Inn(G) trivijalna grupa koja je ciklička jer ju generira identiteta.
Možeš koristiti i jednostavniji argument. ceps i kikzmyster su s nešto manje mašinerije pokazali da je Inn(Z9) zapravo trivijalna grupa, pa je zbog toga ta grupa ciklička.
| Citat: | Ali pod b.) mi nije jasan. Zapravo, da bi bolje objasnio svoje neznanje, nije mi jasna upotreba direktne sume produkta.
Što bi to bilo Z(direktna suma produkta)Z? |
Termin direktna suma produkta nije dobar, kaže se samo direktna suma. Ne trebaš previše razbijati glavu oko toga - kada je konačno mnogo sumanada, onda je direktna suma ekvivalentna direktnom produktu, a koristimo oznaku  umjesto X jer radimo s abelovim grupama. umjesto X jer radimo s abelovim grupama.
| Citat: | Kada bih to znao možda bi znao i odredit Int i Aut od toga...
I odmah da kažem hvala na pomoći...(a sad onda želim pitat sve što mi nije jasno-ali samo iz algebarskih  ) )
 |
Dakle, [tex]\mathbb{Z}\oplus \mathbb{Z}=\left\{(a,b)|a\in\mathbb{Z},b\in\mathbb{Z}\right\}[/tex] i to je grupa s obzirom na operaciju zbrajanja po koordinatama, tj. (a,b)+(c,d)=(a+c,b+d). Neutralni element je (0,0), a inverz od (a,b) je (-a,-b).
_________________
The Dude Abides
Zadnja promjena: goranm; 19:18 sri, 18. 4. 2012; ukupno mijenjano 1 put.
|
|
| [Vrh] |
|
ceps
Forumaš(ica)

Pridružen/a: 08. 10. 2010. (13:03:07)
Postovi: (13A)16
|
 Postano: 19:16 sri, 18. 4. 2012 Naslov: Postano: 19:16 sri, 18. 4. 2012 Naslov: |
    |
|
|
[quote="kkarlo"][quote="ceps"]Ovdje bi se trebalo zaključiti da je [latex]Int(\mathbb{Z}_9) = \{id\}[/latex], samo da to bude jasno.
A ne znam kakav bi ti primjer želio...
[b]Ako ti nešto nije jasno, slobodno pitaj.[/b] :)[/quote]
Jasno mi je...ili barem jasnije nego li mi je prije bilo...
a sad dalje:
http://web.math.pmf.unizg.hr/nastava/alg/2008-09/kolokvij200409.pdf
To je 3 zadatak pod a)
Za Aut(Z9) mi je jasno, i znam ih odredit, i onda bi valjda odgovor bio da to jesu cikličke grupe pošto za svaki Aut(Z9) postoji generator kojim se može generirati cijeli Z9, a i kod Int(Z9) imamo opet Z9 koji je ciklička grupa...Pa onda jesu.
Ali pod b.) mi nije jasan. Zapravo, da bi bolje objasnio svoje neznanje, nije mi jasna upotreba direktne sume produkta.
Što bi to bilo Z(direktna suma produkta)Z?
Kada bih to znao možda bi znao i odredit Int i Aut od toga...
I odmah da kažem hvala na pomoći...(a sad onda želim pitat sve što mi nije jasno-ali samo iz algebarskih :lol: )
:D[/quote]
Prvo ću pod b)
Pa evo, jedan konkretan primjer da bolje ''osjetiš'' tu direktnu sumu, dva elementa i njihov zbroj:
[latex](1, 2) + (3, 5) = (1 + 3, 2 + 5) = (4, 7)[/latex]
Sad malo jasnije o čemu se tu radi? :)
Za a) mi i nije baš jasna tvoja argumentacija, pogotovo kad kažeš da za svaki [latex]Aut(\mathbb{Z}_9)[/latex] postoji generator kojim se može generirati cijeli [latex]\mathbb{Z}_9[/latex]?
Što si tu mislio?
[latex]Aut(\mathbb{Z}_9)[/latex] je skup svih izomorfizama koji idu sa [latex]\mathbb{Z}_9[/latex] u [latex]\mathbb{Z}_9[/latex].
Znači, u [latex]Aut(\mathbb{Z}_9)[/latex], grubo rečeno, ''žive'' funkcije.
Operacija definirana na [latex]Aut(\mathbb{Z}_9)[/latex] je operacija komponiranja.
Ako sam ispravno skužio što si mislio reći gore, ti poistovjećuješ elemente iz [latex]\mathbb{Z}_9[/latex] sa funkcijama, što nikako nije dobro.
Kad te se pita da li je [latex]Aut(\mathbb{Z}_9)[/latex] ciklička, ustvari te se pita postoji li izomorfizam sa [latex]\mathbb{Z}_9[/latex] u [latex]\mathbb{Z}_9[/latex] koji generira sve izomorfizme koji idu sa [latex]\mathbb{Z}_9[/latex] u [latex]\mathbb{Z}_9[/latex] (uz operaciju komponiranja).
| kkarlo (napisa): | | ceps (napisa): | Ovdje bi se trebalo zaključiti da je 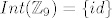 , samo da to bude jasno. , samo da to bude jasno.
A ne znam kakav bi ti primjer želio...
Ako ti nešto nije jasno, slobodno pitaj.  |
Jasno mi je...ili barem jasnije nego li mi je prije bilo...
a sad dalje:
http://web.math.pmf.unizg.hr/nastava/alg/2008-09/kolokvij200409.pdf
To je 3 zadatak pod a)
Za Aut(Z9) mi je jasno, i znam ih odredit, i onda bi valjda odgovor bio da to jesu cikličke grupe pošto za svaki Aut(Z9) postoji generator kojim se može generirati cijeli Z9, a i kod Int(Z9) imamo opet Z9 koji je ciklička grupa...Pa onda jesu.
Ali pod b.) mi nije jasan. Zapravo, da bi bolje objasnio svoje neznanje, nije mi jasna upotreba direktne sume produkta.
Što bi to bilo Z(direktna suma produkta)Z?
Kada bih to znao možda bi znao i odredit Int i Aut od toga...
I odmah da kažem hvala na pomoći...(a sad onda želim pitat sve što mi nije jasno-ali samo iz algebarskih  ) )
 |
Prvo ću pod b)
Pa evo, jedan konkretan primjer da bolje ''osjetiš'' tu direktnu sumu, dva elementa i njihov zbroj:
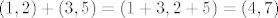
Sad malo jasnije o čemu se tu radi? 
Za a) mi i nije baš jasna tvoja argumentacija, pogotovo kad kažeš da za svaki  postoji generator kojim se može generirati cijeli postoji generator kojim se može generirati cijeli  ? ?
Što si tu mislio?
 je skup svih izomorfizama koji idu sa je skup svih izomorfizama koji idu sa  u u  . .
Znači, u  , grubo rečeno, ''žive'' funkcije. , grubo rečeno, ''žive'' funkcije.
Operacija definirana na  je operacija komponiranja. je operacija komponiranja.
Ako sam ispravno skužio što si mislio reći gore, ti poistovjećuješ elemente iz  sa funkcijama, što nikako nije dobro. sa funkcijama, što nikako nije dobro.
Kad te se pita da li je  ciklička, ustvari te se pita postoji li izomorfizam sa ciklička, ustvari te se pita postoji li izomorfizam sa  u u  koji generira sve izomorfizme koji idu sa koji generira sve izomorfizme koji idu sa  u u  (uz operaciju komponiranja). (uz operaciju komponiranja).
|
|
| [Vrh] |
|
kkarlo
Forumaš(ica)

Pridružen/a: 19. 05. 2010. (08:43:59)
Postovi: (1B2)16
Spol: 
|
 Postano: 22:04 sri, 18. 4. 2012 Naslov: Postano: 22:04 sri, 18. 4. 2012 Naslov: |
    |
|
|
[quote="ceps"][quote="kkarlo"][quote="ceps"]Ovdje bi se trebalo zaključiti da je [latex]Int(\mathbb{Z}_9) = \{id\}[/latex], samo da to bude jasno.
A ne znam kakav bi ti primjer želio...
[b]Ako ti nešto nije jasno, slobodno pitaj.[/b] :)[/quote]
Jasno mi je...ili barem jasnije nego li mi je prije bilo...
a sad dalje:
http://web.math.pmf.unizg.hr/nastava/alg/2008-09/kolokvij200409.pdf
To je 3 zadatak pod a)
Za Aut(Z9) mi je jasno, i znam ih odredit, i onda bi valjda odgovor bio da to jesu cikličke grupe pošto za svaki Aut(Z9) postoji generator kojim se može generirati cijeli Z9, a i kod Int(Z9) imamo opet Z9 koji je ciklička grupa...Pa onda jesu.
Ali pod b.) mi nije jasan. Zapravo, da bi bolje objasnio svoje neznanje, nije mi jasna upotreba direktne sume produkta.
Što bi to bilo Z(direktna suma produkta)Z?
Kada bih to znao možda bi znao i odredit Int i Aut od toga...
I odmah da kažem hvala na pomoći...(a sad onda želim pitat sve što mi nije jasno-ali samo iz algebarskih :lol: )
:D[/quote]
Prvo ću pod b)
Pa evo, jedan konkretan primjer da bolje ''osjetiš'' tu direktnu sumu, dva elementa i njihov zbroj:
[latex](1, 2) + (3, 5) = (1 + 3, 2 + 5) = (4, 7)[/latex]
Sad malo jasnije o čemu se tu radi? :)
Za a) mi i nije baš jasna tvoja argumentacija, pogotovo kad kažeš da za svaki [latex]Aut(\mathbb{Z}_9)[/latex] postoji generator kojim se može generirati cijeli [latex]\mathbb{Z}_9[/latex]?
Što si tu mislio?
[latex]Aut(\mathbb{Z}_9)[/latex] je skup svih izomorfizama koji idu sa [latex]\mathbb{Z}_9[/latex] u [latex]\mathbb{Z}_9[/latex].
Znači, u [latex]Aut(\mathbb{Z}_9)[/latex], grubo rečeno, ''žive'' funkcije.
Operacija definirana na [latex]Aut(\mathbb{Z}_9)[/latex] je operacija komponiranja.
Ako sam ispravno skužio što si mislio reći gore, ti poistovjećuješ elemente iz [latex]\mathbb{Z}_9[/latex] sa funkcijama, što nikako nije dobro.
Kad te se pita da li je [latex]Aut(\mathbb{Z}_9)[/latex] ciklička, ustvari te se pita postoji li izomorfizam sa [latex]\mathbb{Z}_9[/latex] u [latex]\mathbb{Z}_9[/latex] koji generira sve izomorfizme koji idu sa [latex]\mathbb{Z}_9[/latex] u [latex]\mathbb{Z}_9[/latex] (uz operaciju komponiranja).[/quote]
Ma ni sam neznam što sam mislio gore...
Ali sve je ok, uz tvoju pomoć i pomoć goranm-a sam shvatio neke stvari... Zapravo, sve što me je mučilo...zasad.
Sutra je novi dan, pa vjerojatno i nova pitanja.
Još jednom, hvala na pomoći!
| ceps (napisa): | | kkarlo (napisa): | | ceps (napisa): | Ovdje bi se trebalo zaključiti da je 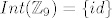 , samo da to bude jasno. , samo da to bude jasno.
A ne znam kakav bi ti primjer želio...
Ako ti nešto nije jasno, slobodno pitaj.  |
Jasno mi je...ili barem jasnije nego li mi je prije bilo...
a sad dalje:
http://web.math.pmf.unizg.hr/nastava/alg/2008-09/kolokvij200409.pdf
To je 3 zadatak pod a)
Za Aut(Z9) mi je jasno, i znam ih odredit, i onda bi valjda odgovor bio da to jesu cikličke grupe pošto za svaki Aut(Z9) postoji generator kojim se može generirati cijeli Z9, a i kod Int(Z9) imamo opet Z9 koji je ciklička grupa...Pa onda jesu.
Ali pod b.) mi nije jasan. Zapravo, da bi bolje objasnio svoje neznanje, nije mi jasna upotreba direktne sume produkta.
Što bi to bilo Z(direktna suma produkta)Z?
Kada bih to znao možda bi znao i odredit Int i Aut od toga...
I odmah da kažem hvala na pomoći...(a sad onda želim pitat sve što mi nije jasno-ali samo iz algebarskih  ) )
 |
Prvo ću pod b)
Pa evo, jedan konkretan primjer da bolje ''osjetiš'' tu direktnu sumu, dva elementa i njihov zbroj:
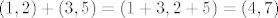
Sad malo jasnije o čemu se tu radi? 
Za a) mi i nije baš jasna tvoja argumentacija, pogotovo kad kažeš da za svaki  postoji generator kojim se može generirati cijeli postoji generator kojim se može generirati cijeli  ? ?
Što si tu mislio?
 je skup svih izomorfizama koji idu sa je skup svih izomorfizama koji idu sa  u u  . .
Znači, u  , grubo rečeno, ''žive'' funkcije. , grubo rečeno, ''žive'' funkcije.
Operacija definirana na  je operacija komponiranja. je operacija komponiranja.
Ako sam ispravno skužio što si mislio reći gore, ti poistovjećuješ elemente iz  sa funkcijama, što nikako nije dobro. sa funkcijama, što nikako nije dobro.
Kad te se pita da li je  ciklička, ustvari te se pita postoji li izomorfizam sa ciklička, ustvari te se pita postoji li izomorfizam sa  u u  koji generira sve izomorfizme koji idu sa koji generira sve izomorfizme koji idu sa  u u  (uz operaciju komponiranja). (uz operaciju komponiranja). |
Ma ni sam neznam što sam mislio gore...
Ali sve je ok, uz tvoju pomoć i pomoć goranm-a sam shvatio neke stvari... Zapravo, sve što me je mučilo...zasad.
Sutra je novi dan, pa vjerojatno i nova pitanja.
Još jednom, hvala na pomoći!
|
|
| [Vrh] |
|
kkarlo
Forumaš(ica)

Pridružen/a: 19. 05. 2010. (08:43:59)
Postovi: (1B2)16
Spol: 
|
 Postano: 9:58 čet, 19. 4. 2012 Naslov: Postano: 9:58 čet, 19. 4. 2012 Naslov: |
    |
|
|
Evo novog pitanja, sa nastavničkog kolokvija:
Postoji li konačna grupa G koja ima nekomutativnu normalnu podgrupu N takvu da je indeks od N u G jednak 2?
E sad, sa tim indeksima....
Jasno mi je da |N| da je to broj elemenata u podgrupi N, i da je |G| broj elemenata u grupi G, i sada definiramo |G/N| kao broj elemenata u toj grupi, i to označavamo sa (G:N).
E sada kada se kaže da je indeks od N u G jednak 2, da li se onda misli na (G:N)=2?*
I onda imam zapisano da je (G:N) broj klasa...i sad me to muči da li je to broj klasa ili broj elemenata?
I ako netko može rješiti ovo gore to bi bilo super...
:)
EDIT:
Evo još jedan sličan, mislim isto sa tim indeksima:
Postoji li konačna grupa G takva da je indeks centra Z(G) u G jednak 2; tj. tako da je (G:Z(G))=2.
Sad sam dobio odgovor na *.
Evo novog pitanja, sa nastavničkog kolokvija:
Postoji li konačna grupa G koja ima nekomutativnu normalnu podgrupu N takvu da je indeks od N u G jednak 2?
E sad, sa tim indeksima....
Jasno mi je da |N| da je to broj elemenata u podgrupi N, i da je |G| broj elemenata u grupi G, i sada definiramo |G/N| kao broj elemenata u toj grupi, i to označavamo sa (G:N).
E sada kada se kaže da je indeks od N u G jednak 2, da li se onda misli na (G:N)=2?*
I onda imam zapisano da je (G:N) broj klasa...i sad me to muči da li je to broj klasa ili broj elemenata?
I ako netko može rješiti ovo gore to bi bilo super...

EDIT:
Evo još jedan sličan, mislim isto sa tim indeksima:
Postoji li konačna grupa G takva da je indeks centra Z(G) u G jednak 2; tj. tako da je (G:Z(G))=2.
Sad sam dobio odgovor na *.
|
|
| [Vrh] |
|
niveus
Forumaš(ica)

Pridružen/a: 26. 10. 2009. (16:12:58)
Postovi: (5E)16
|
|
| [Vrh] |
|
kkarlo
Forumaš(ica)

Pridružen/a: 19. 05. 2010. (08:43:59)
Postovi: (1B2)16
Spol: 
|
 Postano: 11:16 čet, 19. 4. 2012 Naslov: Postano: 11:16 čet, 19. 4. 2012 Naslov: |
    |
|
|
[quote="niveus"]jel može netko objasniti kako se odrežuje Aut(Z10)
hvala :)[/quote]
Mogu ja probat, posto mislim da bi trebalo bit tocno...(ispravite me ako nije)
Znaci prvo odredis generatore od Z10 a to su (1,3,7,9), kako sam saznao, to su svi relativno prosti sa 10, pa ih tako jednostavno odredis!
Sad kad ih imas onda definiras slijedeca preslikavanja
f1(x)=x,f3(x)=3x,f7(x)=7x i f9(x)=9x.
Zasto bas tako, zato sto 0 mora ic u 0 jer je to neutralni element, pa se mora preslikati u neutralni, a posto je 1 generator onda se on mora preslikati u drugi generator, jer inace ne bio izomorfizam, sto Aut je. Posto je Aut(Z10) skup preslikavanja onda smo valjda gotovi, ali evo jos kako bi to izgledalo:
recimo za f3(x)=3x,
(1 ide u 3,3 ide u 9, 9 ide u 7, 7 ide u 1)(2 ide u 6, 6 ide u 8, 8 ide u 4, 4 ide u 2)
i tako mozes za sve ove f-ove koje sam napisao gore napravit...
| niveus (napisa): | jel može netko objasniti kako se odrežuje Aut(Z10)
hvala  |
Mogu ja probat, posto mislim da bi trebalo bit tocno...(ispravite me ako nije)
Znaci prvo odredis generatore od Z10 a to su (1,3,7,9), kako sam saznao, to su svi relativno prosti sa 10, pa ih tako jednostavno odredis!
Sad kad ih imas onda definiras slijedeca preslikavanja
f1(x)=x,f3(x)=3x,f7(x)=7x i f9(x)=9x.
Zasto bas tako, zato sto 0 mora ic u 0 jer je to neutralni element, pa se mora preslikati u neutralni, a posto je 1 generator onda se on mora preslikati u drugi generator, jer inace ne bio izomorfizam, sto Aut je. Posto je Aut(Z10) skup preslikavanja onda smo valjda gotovi, ali evo jos kako bi to izgledalo:
recimo za f3(x)=3x,
(1 ide u 3,3 ide u 9, 9 ide u 7, 7 ide u 1)(2 ide u 6, 6 ide u 8, 8 ide u 4, 4 ide u 2)
i tako mozes za sve ove f-ove koje sam napisao gore napravit...
|
|
| [Vrh] |
|
homoviator
Forumaš(ica)
Pridružen/a: 31. 01. 2011. (18:42:32)
Postovi: (3A)16
|
|
| [Vrh] |
|
niveus
Forumaš(ica)

Pridružen/a: 26. 10. 2009. (16:12:58)
Postovi: (5E)16
|
|
| [Vrh] |
|
kkarlo
Forumaš(ica)

Pridružen/a: 19. 05. 2010. (08:43:59)
Postovi: (1B2)16
Spol: 
|
 Postano: 13:27 čet, 19. 4. 2012 Naslov: Postano: 13:27 čet, 19. 4. 2012 Naslov: |
    |
|
|
[quote="niveus"]hvala kkarlo :D
kako da provjerim ako je Aut(Z10) ciklička ?[/quote]
Opet nisam siguran da li je slijedeća informacija točna ali evo što sam zaključio čitajući goranm-ov post...
Znači goranm kaže ovako:
"Grupa Aut(Z9) će biti ciklička ako potoji element u Aut(Z9) koji generira čitav Aut(Z9), a ne Z9. Koji su sve izomorfizmi u toj grupi? Možeš li s nekim izomorfizmom generirati čitav Aut(Z9)?"
Pa sad ako su ono nabrojani gore svi izomorfizmi oni (f1,f3,f7,f9) onda sigurno možeš generirat f3 preko f1, f3=f1+f1+f1, i tako i f7 i f9, pa je zbog toga ciklička jer postoji jedan element(u ovom slučaju to je funkcija, al nema veze) kojim se može generirati cijeli Aut(Z10)
Tj. to bi bilo ovako: Aut(Z10)=<f1>
opet ću reći, nisam siguran da je to dobro...al valjda je!
:P
EDIT:
Bojim se da sam bio u krivu, ali da me nitko nije ispravio...
Pošto se na Aut(Z9) gleda operacija komponiranja, onda nemožemo gledati f3=f1+f1+f1, nego možemo gledati da se pomoću f3 mogu generirati sve ostale jer ako uzmemo (f3)o(f3)=f9, (f3)o(f3)of(3)=f7 i (f3)o(f3)o(f3)o(f3)=f1...
Pa je Aut(Z10)=<f3>, pa je ciklička.
Valjda, ali mi sad to ipak ima više smisla.
valjda tako.
| niveus (napisa): | hvala kkarlo 
kako da provjerim ako je Aut(Z10) ciklička ? |
Opet nisam siguran da li je slijedeća informacija točna ali evo što sam zaključio čitajući goranm-ov post...
Znači goranm kaže ovako:
"Grupa Aut(Z9) će biti ciklička ako potoji element u Aut(Z9) koji generira čitav Aut(Z9), a ne Z9. Koji su sve izomorfizmi u toj grupi? Možeš li s nekim izomorfizmom generirati čitav Aut(Z9)?"
Pa sad ako su ono nabrojani gore svi izomorfizmi oni (f1,f3,f7,f9) onda sigurno možeš generirat f3 preko f1, f3=f1+f1+f1, i tako i f7 i f9, pa je zbog toga ciklička jer postoji jedan element(u ovom slučaju to je funkcija, al nema veze) kojim se može generirati cijeli Aut(Z10)
Tj. to bi bilo ovako: Aut(Z10)=<f1>
opet ću reći, nisam siguran da je to dobro...al valjda je!

EDIT:
Bojim se da sam bio u krivu, ali da me nitko nije ispravio...
Pošto se na Aut(Z9) gleda operacija komponiranja, onda nemožemo gledati f3=f1+f1+f1, nego možemo gledati da se pomoću f3 mogu generirati sve ostale jer ako uzmemo (f3)o(f3)=f9, (f3)o(f3)of(3)=f7 i (f3)o(f3)o(f3)o(f3)=f1...
Pa je Aut(Z10)=<f3>, pa je ciklička.
Valjda, ali mi sad to ipak ima više smisla.
valjda tako.
|
|
| [Vrh] |
|
goranm
Forumaš(ica)


Pridružen/a: 12. 11. 2002. (20:09:12)
Postovi: (906)16
Spol: 
|
 Postano: 7:21 pet, 20. 4. 2012 Naslov: Postano: 7:21 pet, 20. 4. 2012 Naslov: |
    |
|
|
[quote="kkarlo"]Postoji li konačna grupa G koja ima nekomutativnu normalnu podgrupu N takvu da je indeks od N u G jednak 2?[/quote]
Postoji, i to beskonačno mnogo njih. Za svaki [tex]n\in\mathbb{N}[/tex], alternirajuća grupa [tex]A_n[/tex] reda n normalna je u simetričnoj grupi [tex]S_n[/tex] reda n i vrijedi [tex][S_n:A_n]=2[/tex]. Za n > 3 alternirajuće grupe reda n su nekomutativne pa je jedan primjer [tex]G=S_4[/tex] i [tex]N=A_4[/tex].
[quote]E sad, sa tim indeksima....
Jasno mi je da |N| da je to broj elemenata u podgrupi N, i da je |G| broj elemenata u grupi G, i sada definiramo |G/N| kao broj elemenata u toj grupi, i to označavamo sa (G:N).
E sada kada se kaže da je indeks od N u G jednak 2, da li se onda misli na (G:N)=2?*
I onda imam zapisano da je (G:N) broj klasa...i sad me to muči da li je to broj klasa ili broj elemenata?
I ako netko može rješiti ovo gore to bi bilo super...
:)[/quote]
Dobro si pohvatao. Po definiciji skup G/H je skup svih lijevih klasa od H u G. Kardinalni broj tog skupa označavamo s |G/H|. Isto tako, po definicij je skup H/G skup svih desnih klasa od H u G. Kardinalni broj tog skupa označavamo s |H/G|. Zato što lijevih klasa ima isto koliko i desnih (samo su kardinalni brojevi jednaki! Elementi u tim klasama se podudaraju ako i samo ako je H normalna u G), onda broj lijevih ili desnih klasa od H u G označavamo s (G:H).
[quote]EDIT:
Evo još jedan sličan, mislim isto sa tim indeksima:
Postoji li konačna grupa G takva da je indeks centra Z(G) u G jednak 2; tj. tako da je (G:Z(G))=2.
Sad sam dobio odgovor na *.[/quote]
EDIT: Ovo što je pod spoiler je moje pogrešno zaključivanje. Gost u sljedećem postu daje ispravan odgovor da takva grupa ne može postojati.
[spoiler]
Slično kao i ranije, neka je [tex]G=S_3[/tex]. Znamo da je [tex]A_3[/tex] komutativna i da je [tex][S_3:A_3]=2[/tex]. Trebamo još samo pokazati da je centar od [tex]S_3[/tex] upravo [tex]A_3[/tex].
Znamo da [tex]S_3[/tex] nije komutativna i da je [tex]|S_3|=3!=6[/tex] pa centar od [tex]S_3[/tex] mora imati manje od 6 elemenata (jer inače bi [tex]S_3[/tex] bila komutativna). Dakle, centar od [tex]S_3[/tex] je prava podgrupa od [tex]S_3[/tex] pa red centra može biti 1, 2 ili 3.
Ali, znamo da je [tex]A_3[/tex] komutativna i da je [tex]|A_3|=3!/2=3[/tex] pa onda centar od [tex]S_3[/tex] mora sadržavati sve elemente od [tex]A_3[/tex], tj. mora biti reda barem 3. Dakle, centar od [tex]S_3[/tex] može s jedne strane biti reda 1, 2 ili 3, a s druge strane reda barem 3 pa prema tome centar od [tex]S_3[/tex] mora biti reda točno 3.
Dakle, zasad smo pokazali samo da centar [tex]Z(S_3)[/tex] od [tex]S_3[/tex] ima jednako mnogo elemenata koliko i [tex]A_3[/tex], ali nismo još pokazali da je [tex]Z(S_3)\cong A_3[/tex].
Ali, to je jednostavno: kako su [tex]Z(S_3)[/tex] i [tex]A_3[/tex] grupe reda 3, a jedina grupa reda 3 je [tex]\mathbb{Z}_3[/tex], onda mora biti [tex]Z(S_3)\cong \mathbb{Z}_3\cong A_3[/tex] pa je [tex]Z(S_3)\cong A_3[/tex].[/spoiler]
[size=9][color=#999999]Added after 5 minutes:[/color][/size]
[quote="kkarlo"]Posto je Aut(Z10) skup preslikavanja onda smo valjda gotovi[/quote]
Nismo još gotovi. Treba odrediti koja je to grupa (tj. kojoj od poznatih grupa je izomorfna), a ne samo koji je skup. Kasnije si pokazao da se Aut(Z10) može generirati automorfizmom f3, tj. Aut(Z10) je ciklička i reda je 4, a jedina ciklička grupa reda 4 je [tex]\mathbb{Z}_4[/tex]. Prema tome, [tex]\text{Aut}(\mathbb{Z}_{10})\cong \mathbb{Z}_4[/tex].
[size=9][color=#999999]Added after 48 minutes:[/color][/size]
[quote="homoviator"]Neka n ϵ N i ( G, •) grupa reda 2n+1. Dokažite da tada svaki elem iz G ima jedinstveni drugi korijen , tj.
Za svaki a ϵ G Ǝ!b ϵ G t.d. b2 =a.
Treba li napraviti neki automorfizam od G ili preko svojstava grupe i reda grupe?[/quote]
Teško da ćeš uspjeti napravit koristan automorfizam jer jedina očita funkcija koja bi pomogla je f:G->G, f(g)=g^2, a ona ne mora biti niti homomorfizam kada G nije abelova.
Ono što ti može pomoći je činjenica da red svakog elementa mora dijeliti red grupe pa onda red svakog a iz G mora biti neparan, tj. postoji [tex]m \in \mathbb{N},m\leq n[/tex] td. je [tex]a^{2m+1}=e[/tex].
| kkarlo (napisa): | | Postoji li konačna grupa G koja ima nekomutativnu normalnu podgrupu N takvu da je indeks od N u G jednak 2? |
Postoji, i to beskonačno mnogo njih. Za svaki [tex]n\in\mathbb{N}[/tex], alternirajuća grupa [tex]A_n[/tex] reda n normalna je u simetričnoj grupi [tex]S_n[/tex] reda n i vrijedi [tex][S_n:A_n]=2[/tex]. Za n > 3 alternirajuće grupe reda n su nekomutativne pa je jedan primjer [tex]G=S_4[/tex] i [tex]N=A_4[/tex].
| Citat: | E sad, sa tim indeksima....
Jasno mi je da |N| da je to broj elemenata u podgrupi N, i da je |G| broj elemenata u grupi G, i sada definiramo |G/N| kao broj elemenata u toj grupi, i to označavamo sa (G:N).
E sada kada se kaže da je indeks od N u G jednak 2, da li se onda misli na (G:N)=2?*
I onda imam zapisano da je (G:N) broj klasa...i sad me to muči da li je to broj klasa ili broj elemenata?
I ako netko može rješiti ovo gore to bi bilo super...
 |
Dobro si pohvatao. Po definiciji skup G/H je skup svih lijevih klasa od H u G. Kardinalni broj tog skupa označavamo s |G/H|. Isto tako, po definicij je skup H/G skup svih desnih klasa od H u G. Kardinalni broj tog skupa označavamo s |H/G|. Zato što lijevih klasa ima isto koliko i desnih (samo su kardinalni brojevi jednaki! Elementi u tim klasama se podudaraju ako i samo ako je H normalna u G), onda broj lijevih ili desnih klasa od H u G označavamo s (G:H).
| Citat: | EDIT:
Evo još jedan sličan, mislim isto sa tim indeksima:
Postoji li konačna grupa G takva da je indeks centra Z(G) u G jednak 2; tj. tako da je (G:Z(G))=2.
Sad sam dobio odgovor na *. |
EDIT: Ovo što je pod spoiler je moje pogrešno zaključivanje. Gost u sljedećem postu daje ispravan odgovor da takva grupa ne može postojati.
| Spoiler [hidden; click to show]: |
Slično kao i ranije, neka je [tex]G=S_3[/tex]. Znamo da je [tex]A_3[/tex] komutativna i da je [tex][S_3:A_3]=2[/tex]. Trebamo još samo pokazati da je centar od [tex]S_3[/tex] upravo [tex]A_3[/tex].
Znamo da [tex]S_3[/tex] nije komutativna i da je [tex]|S_3|=3!=6[/tex] pa centar od [tex]S_3[/tex] mora imati manje od 6 elemenata (jer inače bi [tex]S_3[/tex] bila komutativna). Dakle, centar od [tex]S_3[/tex] je prava podgrupa od [tex]S_3[/tex] pa red centra može biti 1, 2 ili 3.
Ali, znamo da je [tex]A_3[/tex] komutativna i da je [tex]|A_3|=3!/2=3[/tex] pa onda centar od [tex]S_3[/tex] mora sadržavati sve elemente od [tex]A_3[/tex], tj. mora biti reda barem 3. Dakle, centar od [tex]S_3[/tex] može s jedne strane biti reda 1, 2 ili 3, a s druge strane reda barem 3 pa prema tome centar od [tex]S_3[/tex] mora biti reda točno 3.
Dakle, zasad smo pokazali samo da centar [tex]Z(S_3)[/tex] od [tex]S_3[/tex] ima jednako mnogo elemenata koliko i [tex]A_3[/tex], ali nismo još pokazali da je [tex]Z(S_3)\cong A_3[/tex].
Ali, to je jednostavno: kako su [tex]Z(S_3)[/tex] i [tex]A_3[/tex] grupe reda 3, a jedina grupa reda 3 je [tex]\mathbb{Z}_3[/tex], onda mora biti [tex]Z(S_3)\cong \mathbb{Z}_3\cong A_3[/tex] pa je [tex]Z(S_3)\cong A_3[/tex]. |
Added after 5 minutes:
| kkarlo (napisa): | | Posto je Aut(Z10) skup preslikavanja onda smo valjda gotovi |
Nismo još gotovi. Treba odrediti koja je to grupa (tj. kojoj od poznatih grupa je izomorfna), a ne samo koji je skup. Kasnije si pokazao da se Aut(Z10) može generirati automorfizmom f3, tj. Aut(Z10) je ciklička i reda je 4, a jedina ciklička grupa reda 4 je [tex]\mathbb{Z}_4[/tex]. Prema tome, [tex]\text{Aut}(\mathbb{Z}_{10})\cong \mathbb{Z}_4[/tex].
Added after 48 minutes:
| homoviator (napisa): | Neka n ϵ N i ( G, •) grupa reda 2n+1. Dokažite da tada svaki elem iz G ima jedinstveni drugi korijen , tj.
Za svaki a ϵ G Ǝ!b ϵ G t.d. b2 =a.
Treba li napraviti neki automorfizam od G ili preko svojstava grupe i reda grupe? |
Teško da ćeš uspjeti napravit koristan automorfizam jer jedina očita funkcija koja bi pomogla je f:G→G, f(g)=g^2, a ona ne mora biti niti homomorfizam kada G nije abelova.
Ono što ti može pomoći je činjenica da red svakog elementa mora dijeliti red grupe pa onda red svakog a iz G mora biti neparan, tj. postoji [tex]m \in \mathbb{N},m\leq n[/tex] td. je [tex]a^{2m+1}=e[/tex].
_________________
The Dude Abides
Zadnja promjena: goranm; 15:16 pet, 20. 4. 2012; ukupno mijenjano 2 put/a.
|
|
| [Vrh] |
|
Gost
|
 Postano: 14:47 pet, 20. 4. 2012 Naslov: Postano: 14:47 pet, 20. 4. 2012 Naslov: |
    |
|
|
Ako se ne varam, centar nije jednak alternirajućoj grupi jer:
(1 2 3)(1 2) = (1 3) != (2 3) = (1 2) (1 2 3)
Čini mi se da je pogrešno zaključiti da ako postoji komutativna podgrupa reda k, da centar mora imati barem k elemenata.
Pretpostavimo da je (G : Z) = 2, gdje je Z centar groupe G.
Tada postoji neki element x iz G\Z takav da vrijedi:
G = Z U xZ (disjunktna unija)
Neka je sada g iz G\Z proizvoljan. Tada je g iz xZ, pa postoji z iz Z tako da
g = xz = ( z iz centra ) = zx
=> z = x^(-1) g = g x^(-1)
=> gx = xg ( tj. x komutira sa svaki elementom iz G\Z )
Kako x komutira također i sa svakim iz Z, onda je x iz Z,
a to je kontradikcija.
Ako se ne varam, centar nije jednak alternirajućoj grupi jer:
(1 2 3)(1 2) = (1 3) != (2 3) = (1 2) (1 2 3)
Čini mi se da je pogrešno zaključiti da ako postoji komutativna podgrupa reda k, da centar mora imati barem k elemenata.
Pretpostavimo da je (G : Z) = 2, gdje je Z centar groupe G.
Tada postoji neki element x iz G\Z takav da vrijedi:
G = Z U xZ (disjunktna unija)
Neka je sada g iz G\Z proizvoljan. Tada je g iz xZ, pa postoji z iz Z tako da
g = xz = ( z iz centra ) = zx
=> z = x^(-1) g = g x^(-1)
=> gx = xg ( tj. x komutira sa svaki elementom iz G\Z )
Kako x komutira također i sa svakim iz Z, onda je x iz Z,
a to je kontradikcija.
|
|
| [Vrh] |
|
goranm
Forumaš(ica)


Pridružen/a: 12. 11. 2002. (20:09:12)
Postovi: (906)16
Spol: 
|
|
| [Vrh] |
|
|
















