| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
satja
Forumaš(ica)

Pridružen/a: 16. 05. 2010. (10:44:17)
Postovi: (F1)16
|
 Postano: 9:01 uto, 5. 6. 2012 Naslov: Postano: 9:01 uto, 5. 6. 2012 Naslov: |
    |
|
|
[quote="jabuka"]moze pomoc? 7.a
http://web.math.pmf.unizg.hr/nastava/difraf/int/2007-08/IFVVkol2_2008.pdf[/quote]
Dotična karta je [tex]F(x,y) = (x, y, f(x,y))[/tex], i sad računaš po formuli koja piše u zadatku (ili po "kraćoj verziji" te formule s vježbi koja determinantu pod korijenom računa pomoću skalarnih produkata).
Dotična karta je [tex]F(x,y) = (x, y, f(x,y))[/tex], i sad računaš po formuli koja piše u zadatku (ili po "kraćoj verziji" te formule s vježbi koja determinantu pod korijenom računa pomoću skalarnih produkata).
|
|
| [Vrh] |
|
jabuka
Forumaš(ica)
Pridružen/a: 21. 11. 2009. (15:53:14)
Postovi: (7C)16
|
|
| [Vrh] |
|
maksuti
Forumaš(ica)

Pridružen/a: 31. 05. 2012. (14:44:57)
Postovi: (3)16
|
|
| [Vrh] |
|
pupi
Forumaš(ica)

Pridružen/a: 20. 12. 2009. (11:03:15)
Postovi: (92)16
Spol: 
|
|
| [Vrh] |
|
KG
Forumaš(ica)
Pridružen/a: 26. 01. 2011. (15:50:24)
Postovi: (30)16
Spol: 
|
 Postano: 13:05 uto, 5. 6. 2012 Naslov: Postano: 13:05 uto, 5. 6. 2012 Naslov: |
    |
|
|
[quote="maksuti"]može pomoć oko 2.b) zadatka, http://web.math.pmf.unizg.hr/nastava/difraf/int/2009-10/kolokvij2.pdf
Hvala :)[/quote]
Prvo primjeti da je to paraboloid, ali zakrenut tako da mu je "tjeme" u (0,1,0) i odrezan ravninom y=0. Sada taj skup treba parametrizirati: f(r,fi)=(r*cosfi, 1-r^2, r*sinfi). Tu parametrizaciju uvrstiš u formulu za površinu plohe i to je to
[size=9][color=#999999]Added after 16 minutes:[/color][/size]
[quote="pupi"]http://web.math.pmf.unizg.hr/nastava/difraf/int/2010-11/kolokvij2.pdf
Koje je rjesenje u drugom ? Tnx :)[/quote]
Ja sam koristio Greena i dobio -2
Prvo primjeti da je to paraboloid, ali zakrenut tako da mu je "tjeme" u (0,1,0) i odrezan ravninom y=0. Sada taj skup treba parametrizirati: f(r,fi)=(r*cosfi, 1-r^2, r*sinfi). Tu parametrizaciju uvrstiš u formulu za površinu plohe i to je to
Added after 16 minutes:
| pupi (napisa): | http://web.math.pmf.unizg.hr/nastava/difraf/int/2010-11/kolokvij2.pdf
Koje je rjesenje u drugom ? Tnx  |
Ja sam koristio Greena i dobio -2
|
|
| [Vrh] |
|
maksuti
Forumaš(ica)

Pridružen/a: 31. 05. 2012. (14:44:57)
Postovi: (3)16
|
|
| [Vrh] |
|
pupi
Forumaš(ica)

Pridružen/a: 20. 12. 2009. (11:03:15)
Postovi: (92)16
Spol: 
|
|
| [Vrh] |
|
KG
Forumaš(ica)

Pridružen/a: 26. 01. 2011. (15:50:24)
Postovi: (30)16
Spol: 
|
|
| [Vrh] |
|
hstojanovic
Forumaš(ica)
Pridružen/a: 16. 10. 2010. (18:00:01)
Postovi: (30)16
Spol: 
|
|
| [Vrh] |
|
pmli
Forumaš(ica)

Pridružen/a: 09. 11. 2009. (12:03:05)
Postovi: (2C8)16
Spol: 
|
|
| [Vrh] |
|
hstojanovic
Forumaš(ica)
Pridružen/a: 16. 10. 2010. (18:00:01)
Postovi: (30)16
Spol: 
|
|
| [Vrh] |
|
jabuka
Forumaš(ica)
Pridružen/a: 21. 11. 2009. (15:53:14)
Postovi: (7C)16
|
 Postano: 16:46 uto, 5. 6. 2012 Naslov: Postano: 16:46 uto, 5. 6. 2012 Naslov: |
    |
|
|
[quote="KG"][quote="maksuti"]može pomoć oko 2.b) zadatka, http://web.math.pmf.unizg.hr/nastava/difraf/int/2009-10/kolokvij2.pdf
Hvala :)[/quote]
Prvo primjeti da je to paraboloid, ali zakrenut tako da mu je "tjeme" u (0,1,0) i odrezan ravninom y=0. Sada taj skup treba parametrizirati: f(r,fi)=(r*cosfi, 1-r^2, r*sinfi). Tu parametrizaciju uvrstiš u formulu za površinu plohe i to je to
[size=9][color=#999999]Added after 16 minutes:[/color][/size]
[quote="pupi"]http://web.math.pmf.unizg.hr/nastava/difraf/int/2010-11/kolokvij2.pdf
Koje je rjesenje u drugom ? Tnx :)[/quote]
Ja sam koristio Greena i dobio -2[/quote]
ovaj 2.iz 2011.
jel mozes molim te objasnit kako preko greena racunamo kad nam fali duzina CA da bi imali trokut pa da je onda integral po rubu od omega=integral po "unutrasnjosti" trokutu od dw
hvala
| KG (napisa): |
Prvo primjeti da je to paraboloid, ali zakrenut tako da mu je "tjeme" u (0,1,0) i odrezan ravninom y=0. Sada taj skup treba parametrizirati: f(r,fi)=(r*cosfi, 1-r^2, r*sinfi). Tu parametrizaciju uvrstiš u formulu za površinu plohe i to je to
Added after 16 minutes:
| pupi (napisa): | http://web.math.pmf.unizg.hr/nastava/difraf/int/2010-11/kolokvij2.pdf
Koje je rjesenje u drugom ? Tnx  |
Ja sam koristio Greena i dobio -2 |
ovaj 2.iz 2011.
jel mozes molim te objasnit kako preko greena racunamo kad nam fali duzina CA da bi imali trokut pa da je onda integral po rubu od omega=integral po "unutrasnjosti" trokutu od dw
hvala
|
|
| [Vrh] |
|
KG
Forumaš(ica)

Pridružen/a: 26. 01. 2011. (15:50:24)
Postovi: (30)16
Spol: 
|
 Postano: 17:46 uto, 5. 6. 2012 Naslov: Postano: 17:46 uto, 5. 6. 2012 Naslov: |
    |
|
|
Nadoštukamo rub sa dužinom CA t.d. dobijemo trokut i onda primjenimo greena. Znači označiš sa P i Q ono uz dx i dy. Tada je traženi integral od P dx + Q dy po orijentiranim dužinama od A do B pa od B do C jednak integralu po trokutu ABC od parcijalnih derivacija P i Q minus integral od P dx + Q dy po rubu CA. Znači moraš samo parametrizirat stranicu CA npr sa g(t)=(0, -t) , t od -1 do 1 i to uvrstit pod integral....dobije se (P(0,-t),Q(0,-t)) skalarno sa (0, -1) dt....znači ostane ti samo -Q(0,-t) dt. Izračunaš taj integral i onaj po trokutu i oduzmeš ih.
Nadoštukamo rub sa dužinom CA t.d. dobijemo trokut i onda primjenimo greena. Znači označiš sa P i Q ono uz dx i dy. Tada je traženi integral od P dx + Q dy po orijentiranim dužinama od A do B pa od B do C jednak integralu po trokutu ABC od parcijalnih derivacija P i Q minus integral od P dx + Q dy po rubu CA. Znači moraš samo parametrizirat stranicu CA npr sa g(t)=(0, -t) , t od -1 do 1 i to uvrstit pod integral....dobije se (P(0,-t),Q(0,-t)) skalarno sa (0, -1) dt....znači ostane ti samo -Q(0,-t) dt. Izračunaš taj integral i onaj po trokutu i oduzmeš ih.
|
|
| [Vrh] |
|
kosani
Forumaš(ica)
Pridružen/a: 14. 11. 2010. (21:22:58)
Postovi: (26)16
|
|
| [Vrh] |
|
pmli
Forumaš(ica)

Pridružen/a: 09. 11. 2009. (12:03:05)
Postovi: (2C8)16
Spol: 
|
 Postano: 22:40 uto, 5. 6. 2012 Naslov: Postano: 22:40 uto, 5. 6. 2012 Naslov: |
    |
|
|
[quote="kosani"]http://web.math.pmf.unizg.hr/nastava/difraf/int/zadaca4.pdf
Može li itko riješiti 2.?[/quote]
Iz teorema 20.9 lako slijedi da je [latex]d(\beta \wedge \gamma) = \alpha \wedge \gamma[/latex]. Da se to "okrene", koristiš zadatak 20.4 i linearnost (preciznije, homogenost) od d. Uglavnom, [latex]\gamma \wedge \alpha = d(\pm \beta \wedge \gamma)[/latex], pa je [latex]\gamma \wedge \alpha[/latex] egzaktna.
[quote="kosani"]I može pomoć, kako riješiti 3. Tj. kako integrirati ovo di je dA[/quote]
[latex]dA[/latex] je neka diferencijalna forma (koja ovisi o plohi). Definicija počinje pri dnu 60. stranice (poglavlje 20).
| kosani (napisa): | http://web.math.pmf.unizg.hr/nastava/difraf/int/zadaca4.pdf
Može li itko riješiti 2.? |
Iz teorema 20.9 lako slijedi da je 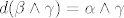 . Da se to "okrene", koristiš zadatak 20.4 i linearnost (preciznije, homogenost) od d. Uglavnom, . Da se to "okrene", koristiš zadatak 20.4 i linearnost (preciznije, homogenost) od d. Uglavnom, 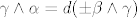 , pa je , pa je 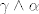 egzaktna. egzaktna.
| kosani (napisa): | | I može pomoć, kako riješiti 3. Tj. kako integrirati ovo di je dA |
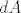 je neka diferencijalna forma (koja ovisi o plohi). Definicija počinje pri dnu 60. stranice (poglavlje 20). je neka diferencijalna forma (koja ovisi o plohi). Definicija počinje pri dnu 60. stranice (poglavlje 20).
|
|
| [Vrh] |
|
satja
Forumaš(ica)

Pridružen/a: 16. 05. 2010. (10:44:17)
Postovi: (F1)16
|
|
| [Vrh] |
|
pmli
Forumaš(ica)

Pridružen/a: 09. 11. 2009. (12:03:05)
Postovi: (2C8)16
Spol: 
|
|
| [Vrh] |
|
|














