| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
angelika
Forumaš(ica)

Pridružen/a: 08. 02. 2011. (17:26:51)
Postovi: (5F)16
|
|
| [Vrh] |
|
sasha.f
Forumaš(ica)

Pridružen/a: 25. 10. 2011. (20:04:19)
Postovi: (3D)16
|
|
| [Vrh] |
|
shimija
Forumaš(ica)


Pridružen/a: 22. 01. 2007. (18:33:54)
Postovi: (138)16
Spol: 
Lokacija: Spljit
|
 Postano: 15:59 uto, 8. 1. 2013 Naslov: Postano: 15:59 uto, 8. 1. 2013 Naslov: |
    |
|
|
Možda bi ovako išlo:
definirajmo
[dtex]A=\{a_1,\dots,a_m\} \ , \ B=\{b_1,\dots,b_n\} \;.[/dtex]
Desna strana je broj k-članih podskupova skupa A.
Lijeva strana je isto, ali preko FUI-a tako da tražimo
broj k-članih podskupova skupa [tex]A\cup B[/tex] koji ne sadrže
niti jedan element iz B.
Definirajmo
[dtex]S_i:=\{C\subseteq A\cup B \ | \ b_i\not\in C \} \;.[/dtex]
Nas zanima [tex]|S_1\cup\dots\cup S_n|[/tex]
Možda bi ovako išlo:
definirajmo
[dtex]A=\{a_1,\dots,a_m\} \ , \ B=\{b_1,\dots,b_n\} \;.[/dtex]
Desna strana je broj k-članih podskupova skupa A.
Lijeva strana je isto, ali preko FUI-a tako da tražimo
broj k-članih podskupova skupa [tex]A\cup B[/tex] koji ne sadrže
niti jedan element iz B.
Definirajmo
[dtex]S_i:=\{C\subseteq A\cup B \ | \ b_i\not\in C \} \;.[/dtex]
Nas zanima [tex]|S_1\cup\dots\cup S_n|[/tex]
|
|
| [Vrh] |
|
PermutiranoPrase
Forumaš(ica)


Pridružen/a: 10. 09. 2011. (16:08:19)
Postovi: (F4)16
Spol: 
|
|
| [Vrh] |
|
Loo
Forumaš(ica)


Pridružen/a: 11. 06. 2012. (16:02:07)
Postovi: (D0)16
Spol: 
|
|
| [Vrh] |
|
PermutiranoPrase
Forumaš(ica)


Pridružen/a: 10. 09. 2011. (16:08:19)
Postovi: (F4)16
Spol: 
|
 Postano: 16:53 sri, 9. 1. 2013 Naslov: Postano: 16:53 sri, 9. 1. 2013 Naslov: |
    |
|
|
Hvala!
Zna li tko riješiti [url=http://web.math.pmf.unizg.hr/nastava/komb/pdf/2008-09/08kol2.pdf]1. i 2. u drugoj grupi[/url], te [url=http://web.math.pmf.unizg.hr/nastava/komb/pdf/2007-08/DM2007kol2.pdf]2.B[/url]?
Problemi su mi redom:
1) Bračne parove rješavam preko FUI, ali ne znam baš kako presjeke odrediti (ispadalo mi je nešto jako komplicirano već za presjek 2 skupa, da sam nastavila bi bio užas, pa nekako mislim da je krivo :) )
2) Je l ovo treba preko EFI? Ako da, radim li, i ako da, kako to prebaciti u red?
[latex]f(x) = (1+x+\frac {x^2}{2}+...+\frac {x^7}{7!})^4[/latex]?
3) Nemam blage kako uopće ovo prikazati preko FUI. :?
Hvala!
Zna li tko riješiti 1. i 2. u drugoj grupi, te 2.B?
Problemi su mi redom:
1) Bračne parove rješavam preko FUI, ali ne znam baš kako presjeke odrediti (ispadalo mi je nešto jako komplicirano već za presjek 2 skupa, da sam nastavila bi bio užas, pa nekako mislim da je krivo  ) )
2) Je l ovo treba preko EFI? Ako da, radim li, i ako da, kako to prebaciti u red?
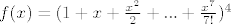 ? ?
3) Nemam blage kako uopće ovo prikazati preko FUI. 
|
|
| [Vrh] |
|
quark
Forumaš(ica)


Pridružen/a: 22. 10. 2011. (16:47:39)
Postovi: (DA)16
Spol: 
|
 Postano: 19:01 sri, 9. 1. 2013 Naslov: Postano: 19:01 sri, 9. 1. 2013 Naslov: |
    |
|
|
[quote="PermutiranoPrase"]Hvala!
Zna li tko riješiti [url=http://web.math.pmf.unizg.hr/nastava/komb/pdf/2008-09/08kol2.pdf]1. i 2. u drugoj grupi[/url], te [url=http://web.math.pmf.unizg.hr/nastava/komb/pdf/2007-08/DM2007kol2.pdf]2.B[/url]?
Problemi su mi redom:
1) Bračne parove rješavam preko FUI, ali ne znam baš kako presjeke odrediti (ispadalo mi je nešto jako komplicirano već za presjek 2 skupa, da sam nastavila bi bio užas, pa nekako mislim da je krivo :) )
2) Je l ovo treba preko EFI? Ako da, radim li, i ako da, kako to prebaciti u red?
[latex]f(x) = (1+x+\frac {x^2}{2}+...+\frac {x^7}{7!})^4[/latex]?
3) Nemam blage kako uopće ovo prikazati preko FUI. :?[/quote]
1.) Hint: deranžmani
2.) Neka je [tex]|A_i|[/tex] broj odabira takav da [tex]x_i[/tex] zadovoljava traženo svojstvo; u zadatku se traži [tex]| \bigcap A_i|[/tex], a to izračunaš preko FUI.
Probaj s time, ali mislim da bi se moglo i preko EFI-ja :D
3.) Neka je [tex]|A_i|[/tex] broj brojeva koji dijeli [tex]i[/tex]-ti zadani broj; tebe zanima [tex]| \bigcup A_i |[/tex]
| PermutiranoPrase (napisa): | Hvala!
Zna li tko riješiti 1. i 2. u drugoj grupi, te 2.B?
Problemi su mi redom:
1) Bračne parove rješavam preko FUI, ali ne znam baš kako presjeke odrediti (ispadalo mi je nešto jako komplicirano već za presjek 2 skupa, da sam nastavila bi bio užas, pa nekako mislim da je krivo  ) )
2) Je l ovo treba preko EFI? Ako da, radim li, i ako da, kako to prebaciti u red?
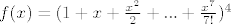 ? ?
3) Nemam blage kako uopće ovo prikazati preko FUI.  |
1.) Hint: deranžmani
2.) Neka je [tex]|A_i|[/tex] broj odabira takav da [tex]x_i[/tex] zadovoljava traženo svojstvo; u zadatku se traži [tex]| \bigcap A_i|[/tex], a to izračunaš preko FUI.
Probaj s time, ali mislim da bi se moglo i preko EFI-ja 
3.) Neka je [tex]|A_i|[/tex] broj brojeva koji dijeli [tex]i[/tex]-ti zadani broj; tebe zanima [tex]| \bigcup A_i |[/tex]
|
|
| [Vrh] |
|
PermutiranoPrase
Forumaš(ica)


Pridružen/a: 10. 09. 2011. (16:08:19)
Postovi: (F4)16
Spol: 
|
|
| [Vrh] |
|
quark
Forumaš(ica)


Pridružen/a: 22. 10. 2011. (16:47:39)
Postovi: (DA)16
Spol: 
|
|
| [Vrh] |
|
27re
Forumaš(ica)


Pridružen/a: 06. 10. 2010. (16:07:02)
Postovi: (17)16
|
|
| [Vrh] |
|
quark
Forumaš(ica)


Pridružen/a: 22. 10. 2011. (16:47:39)
Postovi: (DA)16
Spol: 
|
|
| [Vrh] |
|
homoviator
Forumaš(ica)
Pridružen/a: 31. 01. 2011. (18:42:32)
Postovi: (3A)16
|
|
| [Vrh] |
|
an5
Forumaš(ica)
Pridružen/a: 13. 09. 2012. (20:48:55)
Postovi: (9)16
|
|
| [Vrh] |
|
homoviator
Forumaš(ica)
Pridružen/a: 31. 01. 2011. (18:42:32)
Postovi: (3A)16
|
|
| [Vrh] |
|
Pavlek
Forumaš(ica)

Pridružen/a: 30. 11. 2011. (21:05:53)
Postovi: (E)16
Spol: 
|
|
| [Vrh] |
|
krki
Forumaš(ica)

Pridružen/a: 06. 07. 2011. (20:30:12)
Postovi: (2E)16
|
|
| [Vrh] |
|
Pavlek
Forumaš(ica)

Pridružen/a: 30. 11. 2011. (21:05:53)
Postovi: (E)16
Spol: 
|
 Postano: 15:37 čet, 10. 1. 2013 Naslov: Postano: 15:37 čet, 10. 1. 2013 Naslov: |
    |
|
|
Oprosti, ali zamolio bih, da ako nije problem, da malčice konkretnije objasniš kako dokazati da je K,3,3 podgraf od ovog grafa, jer u K3.3, ako imaš vremena! I hvala na ideji, razmislit ću!
Oprosti, ali zamolio bih, da ako nije problem, da malčice konkretnije objasniš kako dokazati da je K,3,3 podgraf od ovog grafa, jer u K3.3, ako imaš vremena! I hvala na ideji, razmislit ću!
|
|
| [Vrh] |
|
Phoenix
Forumaš(ica)


Pridružen/a: 15. 05. 2010. (18:46:07)
Postovi: (164)16
Sarma: -
|
 Postano: 15:52 čet, 10. 1. 2013 Naslov: Postano: 15:52 čet, 10. 1. 2013 Naslov: |
    |
|
|
@Pavlek: Pretpostavimo da tvrdnja zadatka vrijedi. Neka je [tex]n[/tex] broj vrhova u grafu, a [tex]q[/tex] broj bridova.
Pretpostavimo sada da je graf povezan. (*) Po zadatku [tex]9.16[/tex] s vježbi slijedi da je [tex]q \leq 2n-4[/tex].
Nadalje, u grafu vrijedi da je suma stupnjeva svih vrhova jednaka dvostrukom broju bridova (naime, svaki brid prebrojiš dvaput, za svaki od dva vrha koja povezuje). Zbog pretpostavke iz zadatka, slijedi [tex]2q \geq 4n[/tex], odnosno [tex]q \geq 2n[/tex].
Ukupno, dobili smo [tex]2n \leq q \leq 2n-4[/tex], što je kontradikcija.
Još bih trebao prokomentirati pretpostavku (*), odnosno reći što ako graf nije povezan. Tada graf promatramo kao kolekciju više grafova obzirom na komponente povezanosti (poslije zadatka [tex]3.3[/tex] s predavanja). Za svaki od tih grafova, označimo ih s [tex]G_1,G_2,...,G_k[/tex], pri čemu je [tex]k[/tex] broj "podgrafova", vrijede iste pretpostavke kao i u zadatku, uz dodatnu pretpostavku da je svaki od tih grafova povezan. Sada dalje dobivamo slično rješenje: [tex]2n_i \leq q_i \leq 2n_i-4[/tex], pri čemu su [tex]n_i, q_i[/tex], respektivno, broj vrhova i bridova u [tex]i[/tex]-tom podgrafu.
Zbrojimo li tih [tex]k[/tex] nejednakosti po [tex]i[/tex], dobivamo prijašnji, željeni rezultat: [tex]2n \leq q \leq 2n-4[/tex].
(Vjerojatno sam neprecizno i olako koristio neke pojmove, na čemu se ispričavam, ali ipak pišem ovo rješenje "na brzinu". :P)
Zapravo, na kraju drugog paragrafa nisam trebao ni sumirati po "podgrafovima" kada je kontradikcija dobivena već u jednom od njih, pa je i tu zadatak gotov. No, to sam raspisao jer mi se čini kao zgodna ideja za rješavanje nekih drugih zadataka koji su se znali pojavljivati za vježbu ili u kolokviju (najčešće, kada nemaš pretpostavku o povezanosti grafa, a trebaš je da bi iskoristio željene rezultate s predavanja ili vježbi).
Nadam se da nisam nešto pobrkao. :)
@Pavlek: Pretpostavimo da tvrdnja zadatka vrijedi. Neka je [tex]n[/tex] broj vrhova u grafu, a [tex]q[/tex] broj bridova.
Pretpostavimo sada da je graf povezan. (*) Po zadatku [tex]9.16[/tex] s vježbi slijedi da je [tex]q \leq 2n-4[/tex].
Nadalje, u grafu vrijedi da je suma stupnjeva svih vrhova jednaka dvostrukom broju bridova (naime, svaki brid prebrojiš dvaput, za svaki od dva vrha koja povezuje). Zbog pretpostavke iz zadatka, slijedi [tex]2q \geq 4n[/tex], odnosno [tex]q \geq 2n[/tex].
Ukupno, dobili smo [tex]2n \leq q \leq 2n-4[/tex], što je kontradikcija.
Još bih trebao prokomentirati pretpostavku (*), odnosno reći što ako graf nije povezan. Tada graf promatramo kao kolekciju više grafova obzirom na komponente povezanosti (poslije zadatka [tex]3.3[/tex] s predavanja). Za svaki od tih grafova, označimo ih s [tex]G_1,G_2,...,G_k[/tex], pri čemu je [tex]k[/tex] broj "podgrafova", vrijede iste pretpostavke kao i u zadatku, uz dodatnu pretpostavku da je svaki od tih grafova povezan. Sada dalje dobivamo slično rješenje: [tex]2n_i \leq q_i \leq 2n_i-4[/tex], pri čemu su [tex]n_i, q_i[/tex], respektivno, broj vrhova i bridova u [tex]i[/tex]-tom podgrafu.
Zbrojimo li tih [tex]k[/tex] nejednakosti po [tex]i[/tex], dobivamo prijašnji, željeni rezultat: [tex]2n \leq q \leq 2n-4[/tex].
(Vjerojatno sam neprecizno i olako koristio neke pojmove, na čemu se ispričavam, ali ipak pišem ovo rješenje "na brzinu".  ) )
Zapravo, na kraju drugog paragrafa nisam trebao ni sumirati po "podgrafovima" kada je kontradikcija dobivena već u jednom od njih, pa je i tu zadatak gotov. No, to sam raspisao jer mi se čini kao zgodna ideja za rješavanje nekih drugih zadataka koji su se znali pojavljivati za vježbu ili u kolokviju (najčešće, kada nemaš pretpostavku o povezanosti grafa, a trebaš je da bi iskoristio željene rezultate s predavanja ili vježbi).
Nadam se da nisam nešto pobrkao. 
|
|
| [Vrh] |
|
student_92
Forumaš(ica)

Pridružen/a: 17. 09. 2011. (16:31:46)
Postovi: (B9)16
|
|
| [Vrh] |
|
krki
Forumaš(ica)

Pridružen/a: 06. 07. 2011. (20:30:12)
Postovi: (2E)16
|
 Postano: 16:02 čet, 10. 1. 2013 Naslov: Postano: 16:02 čet, 10. 1. 2013 Naslov: |
    |
|
|
[quote="Pavlek"]Oprosti, ali zamolio bih, da ako nije problem, da malčice konkretnije objasniš kako dokazati da je K,3,3 podgraf od ovog grafa, jer u K3.3, ako imaš vremena! I hvala na ideji, razmislit ću![/quote]
EDIT: nije mi dobra ideja, našao sam si grešku :oops:
| Pavlek (napisa): | | Oprosti, ali zamolio bih, da ako nije problem, da malčice konkretnije objasniš kako dokazati da je K,3,3 podgraf od ovog grafa, jer u K3.3, ako imaš vremena! I hvala na ideji, razmislit ću! |
EDIT: nije mi dobra ideja, našao sam si grešku 
|
|
| [Vrh] |
|
|














