| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
Megy Poe
Forumaš(ica)

Pridružen/a: 05. 11. 2009. (23:14:52)
Postovi: (122)16
|
 Postano: 22:01 sri, 23. 1. 2013 Naslov: Postano: 22:01 sri, 23. 1. 2013 Naslov: |
    |
|
|
Ja imam pitanje s 2. kolokvija 2011. koji kaže da je podskup U totalno uređenog skupa (A,<)otvoren ako za svaki x iz U postoje a,b iz A takvi da je <a,b> iz U i a<x<b. Dokažite da je svojstvo postoji neprazan otvoren skup čiji je komplement ne prazan i otvoren invarijnta sličnosti, te dajte primjer jednog skupa s tim svojstvom.
Ja ne znam nijedan primjer takvog skupa pa ne znam ni ovo dokazati..ima netko primjer?
[size=9][color=#999999]Added after 19 minutes:[/color][/size]
[quote="Megy Poe"]Ja imam pitanje s 2. kolokvija 2011. koji kaže da je podskup U totalno uređenog skupa (A,<)otvoren ako za svaki x iz U postoje a,b iz A takvi da je <a,b> iz U i a<x<b. Dokažite da je svojstvo postoji neprazan otvoren skup čiji je komplement ne prazan i otvoren invarijnta sličnosti, te dajte primjer jednog skupa s tim svojstvom.
Ja ne znam nijedan primjer takvog skupa pa ne znam ni ovo dokazati..ima netko primjer?[/quote]
wuhu sjetih se nakon 1 h pa da si sama odgovorim kad se već ne mogu brisat postovi XD
skup ...<-2,0>U<-1,0>...<2,0>U<3,0> i sad npr podskup <1,0> je otvoren a njegov komplemnt je unija otvorenih skupova pa je također otvoren.
Ja imam pitanje s 2. kolokvija 2011. koji kaže da je podskup U totalno uređenog skupa (A,<)otvoren ako za svaki x iz U postoje a,b iz A takvi da je <a,b> iz U i a<x<b. Dokažite da je svojstvo postoji neprazan otvoren skup čiji je komplement ne prazan i otvoren invarijnta sličnosti, te dajte primjer jednog skupa s tim svojstvom.
Ja ne znam nijedan primjer takvog skupa pa ne znam ni ovo dokazati..ima netko primjer?
Added after 19 minutes:
| Megy Poe (napisa): | Ja imam pitanje s 2. kolokvija 2011. koji kaže da je podskup U totalno uređenog skupa (A,<)otvoren ako za svaki x iz U postoje a,b iz A takvi da je <a,b> iz U i a<x<b. Dokažite da je svojstvo postoji neprazan otvoren skup čiji je komplement ne prazan i otvoren invarijnta sličnosti, te dajte primjer jednog skupa s tim svojstvom.
Ja ne znam nijedan primjer takvog skupa pa ne znam ni ovo dokazati..ima netko primjer? |
wuhu sjetih se nakon 1 h pa da si sama odgovorim kad se već ne mogu brisat postovi XD
skup ...←2,0>U←1,0>...<2,0>U<3,0> i sad npr podskup <1,0> je otvoren a njegov komplemnt je unija otvorenih skupova pa je također otvoren.
|
|
| [Vrh] |
|
Megy Poe
Forumaš(ica)

Pridružen/a: 05. 11. 2009. (23:14:52)
Postovi: (122)16
|
 Postano: 23:45 sri, 23. 1. 2013 Naslov: Postano: 23:45 sri, 23. 1. 2013 Naslov: |
    |
|
|
Jel može pomoć oko 2 zadatka s dosadšnjih kolokvija? Neka je K skup svih konačnih podskupova od n, odredite ako postoji najmanji i najveći element, te sve maksimalne i minimalne elemente u skupovima a) K s obzirom na realciju podskup i b) K/{0} s obzirom na relaciju podskup..
Ja sam zakljucila i pod a) i b) da nema najvećih ni maksimalnih..jel ako je {0,1,2,....n} neki konačan podskup uvijek će imati nadskup npr {0,1,2...n+1} a minimalni elementi su mi svi jednočlani skupovi tj oblika {n} za n iz n pa nema najmanjeg..
al moje rješenje očito nevalja s obzirom da su pitanja pod a i b a meni odgovori isti :D
Drugi zadatak koji me muči je koji su od skupova slični a koji nisu za R/[0,1], R/<-1/2,1/2>, <0,+beskonačno>. Jel po meni nijedan nije sličan s nijednim a to baš očito nema smisla kad je pitanje koji jesu a koji nisu..
Jel može pomoć oko 2 zadatka s dosadšnjih kolokvija? Neka je K skup svih konačnih podskupova od n, odredite ako postoji najmanji i najveći element, te sve maksimalne i minimalne elemente u skupovima a) K s obzirom na realciju podskup i b) K/{0} s obzirom na relaciju podskup..
Ja sam zakljucila i pod a) i b) da nema najvećih ni maksimalnih..jel ako je {0,1,2,....n} neki konačan podskup uvijek će imati nadskup npr {0,1,2...n+1} a minimalni elementi su mi svi jednočlani skupovi tj oblika {n} za n iz n pa nema najmanjeg..
al moje rješenje očito nevalja s obzirom da su pitanja pod a i b a meni odgovori isti 
Drugi zadatak koji me muči je koji su od skupova slični a koji nisu za R/[0,1], R/←1/2,1/2>, <0,+beskonačno>. Jel po meni nijedan nije sličan s nijednim a to baš očito nema smisla kad je pitanje koji jesu a koji nisu..
|
|
| [Vrh] |
|
ceps
Forumaš(ica)

Pridružen/a: 08. 10. 2010. (13:03:07)
Postovi: (13A)16
|
 Postano: 8:02 čet, 24. 1. 2013 Naslov: Postano: 8:02 čet, 24. 1. 2013 Naslov: |
    |
|
|
[quote="Megy Poe"]Jel može pomoć oko 2 zadatka s dosadšnjih kolokvija? Neka je K skup svih konačnih podskupova od n, odredite ako postoji najmanji i najveći element, te sve maksimalne i minimalne elemente u skupovima a) K s obzirom na realciju podskup i b) K/{0} s obzirom na relaciju podskup..
Ja sam zakljucila i pod a) i b) da nema najvećih ni maksimalnih..jel ako je {0,1,2,....n} neki konačan podskup uvijek će imati nadskup npr {0,1,2...n+1} a minimalni elementi su mi svi jednočlani skupovi tj oblika {n} za n iz n pa nema najmanjeg..
al moje rješenje očito nevalja s obzirom da su pitanja pod a i b a meni odgovori isti :D
Drugi zadatak koji me muči je koji su od skupova slični a koji nisu za R/[0,1], R/<-1/2,1/2>, <0,+beskonačno>. Jel po meni nijedan nije sličan s nijednim a to baš očito nema smisla kad je pitanje koji jesu a koji nisu..[/quote]
1. Jel brojimo i [latex]\emptyset[/latex] među konačne skupove? Ako da, onda bi on trebao biti najmanji element, ke ne? Ne mogu nigdje naći taj tvoj zadatak, ali nekako mi se čini da bi ovaj tvoj K/{0} trebao biti [latex]K / \{ \emptyset \}[/latex] i onda odgovor nije baš isti...
2. Po tebi nije niti jedan sličan sa nijednim... a zašto to ne bi bio dobar odgovor? Mislim da je uvijek bolje osloniti se na znanje, nego na neku tvoju približnu ideju ''kako bi odgovor trebao izgledati''.
Ukratko, [latex]<0, \infty>[/latex] je sličan sa [latex]\mathbb{R}[/latex], zbog uređajne karakterizacije realnih brojeva.
[latex]\mathbb{R} /<\frac{-1}{2} , \frac{1}{2}>[/latex] nije sličan sa [latex]\mathbb{R}[/latex] zbog gustoće(baš između ovih ''rubnih točaka'').
[latex]\mathbb{R} /[0,1][/latex] nije sličan sa [latex]\mathbb{R}[/latex] zbog topološke zatvorenosti (uzmi neki niz koji ide u 0 ili u 1...).
I onda se vidi da baš ova svojstva koja ''odvajaju'' ova dva skupa od [latex]\mathbb{R}[/latex] , da ih odvajaju i međusobno: jedan od njih je gust, drugi nije.
| Megy Poe (napisa): | Jel može pomoć oko 2 zadatka s dosadšnjih kolokvija? Neka je K skup svih konačnih podskupova od n, odredite ako postoji najmanji i najveći element, te sve maksimalne i minimalne elemente u skupovima a) K s obzirom na realciju podskup i b) K/{0} s obzirom na relaciju podskup..
Ja sam zakljucila i pod a) i b) da nema najvećih ni maksimalnih..jel ako je {0,1,2,....n} neki konačan podskup uvijek će imati nadskup npr {0,1,2...n+1} a minimalni elementi su mi svi jednočlani skupovi tj oblika {n} za n iz n pa nema najmanjeg..
al moje rješenje očito nevalja s obzirom da su pitanja pod a i b a meni odgovori isti 
Drugi zadatak koji me muči je koji su od skupova slični a koji nisu za R/[0,1], R/←1/2,1/2>, <0,+beskonačno>. Jel po meni nijedan nije sličan s nijednim a to baš očito nema smisla kad je pitanje koji jesu a koji nisu.. |
1. Jel brojimo i  među konačne skupove? Ako da, onda bi on trebao biti najmanji element, ke ne? Ne mogu nigdje naći taj tvoj zadatak, ali nekako mi se čini da bi ovaj tvoj K/{0} trebao biti među konačne skupove? Ako da, onda bi on trebao biti najmanji element, ke ne? Ne mogu nigdje naći taj tvoj zadatak, ali nekako mi se čini da bi ovaj tvoj K/{0} trebao biti 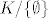 i onda odgovor nije baš isti... i onda odgovor nije baš isti...
2. Po tebi nije niti jedan sličan sa nijednim... a zašto to ne bi bio dobar odgovor? Mislim da je uvijek bolje osloniti se na znanje, nego na neku tvoju približnu ideju ''kako bi odgovor trebao izgledati''.
Ukratko, 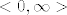 je sličan sa je sličan sa  , zbog uređajne karakterizacije realnih brojeva. , zbog uređajne karakterizacije realnih brojeva.
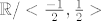 nije sličan sa nije sličan sa  zbog gustoće(baš između ovih ''rubnih točaka''). zbog gustoće(baš između ovih ''rubnih točaka'').
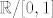 nije sličan sa nije sličan sa  zbog topološke zatvorenosti (uzmi neki niz koji ide u 0 ili u 1...). zbog topološke zatvorenosti (uzmi neki niz koji ide u 0 ili u 1...).
I onda se vidi da baš ova svojstva koja ''odvajaju'' ova dva skupa od  , da ih odvajaju i međusobno: jedan od njih je gust, drugi nije. , da ih odvajaju i međusobno: jedan od njih je gust, drugi nije.
|
|
| [Vrh] |
|
googol
Forumaš(ica)


Pridružen/a: 29. 09. 2011. (21:23:09)
Postovi: (71)16
Spol: 
|
|
| [Vrh] |
|
ceps
Forumaš(ica)

Pridružen/a: 08. 10. 2010. (13:03:07)
Postovi: (13A)16
|
|
| [Vrh] |
|
Megy Poe
Forumaš(ica)

Pridružen/a: 05. 11. 2009. (23:14:52)
Postovi: (122)16
|
 Postano: 20:12 čet, 24. 1. 2013 Naslov: Postano: 20:12 čet, 24. 1. 2013 Naslov: |
    |
|
|
[quote="ceps"][quote="Megy Poe"]Jel može pomoć oko 2 zadatka s dosadšnjih kolokvija? Neka je K skup svih konačnih podskupova od n, odredite ako postoji najmanji i najveći element, te sve maksimalne i minimalne elemente u skupovima a) K s obzirom na realciju podskup i b) K/{0} s obzirom na relaciju podskup..
Ja sam zakljucila i pod a) i b) da nema najvećih ni maksimalnih..jel ako je {0,1,2,....n} neki konačan podskup uvijek će imati nadskup npr {0,1,2...n+1} a minimalni elementi su mi svi jednočlani skupovi tj oblika {n} za n iz n pa nema najmanjeg..
al moje rješenje očito nevalja s obzirom da su pitanja pod a i b a meni odgovori isti :D
Drugi zadatak koji me muči je koji su od skupova slični a koji nisu za R/[0,1], R/<-1/2,1/2>, <0,+beskonačno>. Jel po meni nijedan nije sličan s nijednim a to baš očito nema smisla kad je pitanje koji jesu a koji nisu..[/quote]
1. Jel brojimo i [latex]\emptyset[/latex] među konačne skupove? Ako da, onda bi on trebao biti najmanji element, ke ne? Ne mogu nigdje naći taj tvoj zadatak, ali nekako mi se čini da bi ovaj tvoj K/{0} trebao biti [latex]K / \{ \emptyset \}[/latex] i onda odgovor nije baš isti...
2. Po tebi nije niti jedan sličan sa nijednim... a zašto to ne bi bio dobar odgovor? Mislim da je uvijek bolje osloniti se na znanje, nego na neku tvoju približnu ideju ''kako bi odgovor trebao izgledati''.
Ukratko, [latex]<0, \infty>[/latex] je sličan sa [latex]\mathbb{R}[/latex], zbog uređajne karakterizacije realnih brojeva.
[latex]\mathbb{R} /<\frac{-1}{2} , \frac{1}{2}>[/latex] nije sličan sa [latex]\mathbb{R}[/latex] zbog gustoće(baš između ovih ''rubnih točaka'').
[latex]\mathbb{R} /[0,1][/latex] nije sličan sa [latex]\mathbb{R}[/latex] zbog topološke zatvorenosti (uzmi neki niz koji ide u 0 ili u 1...).
I onda se vidi da baš ova svojstva koja ''odvajaju'' ova dva skupa od [latex]\mathbb{R}[/latex] , da ih odvajaju i međusobno: jedan od njih je gust, drugi nije.[/quote]
Hvala puno! Nisam se sjetila praznog skupa a očito spada jel onda odgovor je različit :D, i asistenti su mi rekli da imam problema sa samopouzdanjem u vezi ovog predmeta XD..
| ceps (napisa): | | Megy Poe (napisa): | Jel može pomoć oko 2 zadatka s dosadšnjih kolokvija? Neka je K skup svih konačnih podskupova od n, odredite ako postoji najmanji i najveći element, te sve maksimalne i minimalne elemente u skupovima a) K s obzirom na realciju podskup i b) K/{0} s obzirom na relaciju podskup..
Ja sam zakljucila i pod a) i b) da nema najvećih ni maksimalnih..jel ako je {0,1,2,....n} neki konačan podskup uvijek će imati nadskup npr {0,1,2...n+1} a minimalni elementi su mi svi jednočlani skupovi tj oblika {n} za n iz n pa nema najmanjeg..
al moje rješenje očito nevalja s obzirom da su pitanja pod a i b a meni odgovori isti 
Drugi zadatak koji me muči je koji su od skupova slični a koji nisu za R/[0,1], R/←1/2,1/2>, <0,+beskonačno>. Jel po meni nijedan nije sličan s nijednim a to baš očito nema smisla kad je pitanje koji jesu a koji nisu.. |
1. Jel brojimo i  među konačne skupove? Ako da, onda bi on trebao biti najmanji element, ke ne? Ne mogu nigdje naći taj tvoj zadatak, ali nekako mi se čini da bi ovaj tvoj K/{0} trebao biti među konačne skupove? Ako da, onda bi on trebao biti najmanji element, ke ne? Ne mogu nigdje naći taj tvoj zadatak, ali nekako mi se čini da bi ovaj tvoj K/{0} trebao biti 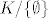 i onda odgovor nije baš isti... i onda odgovor nije baš isti...
2. Po tebi nije niti jedan sličan sa nijednim... a zašto to ne bi bio dobar odgovor? Mislim da je uvijek bolje osloniti se na znanje, nego na neku tvoju približnu ideju ''kako bi odgovor trebao izgledati''.
Ukratko, 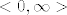 je sličan sa je sličan sa  , zbog uređajne karakterizacije realnih brojeva. , zbog uređajne karakterizacije realnih brojeva.
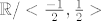 nije sličan sa nije sličan sa  zbog gustoće(baš između ovih ''rubnih točaka''). zbog gustoće(baš između ovih ''rubnih točaka'').
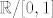 nije sličan sa nije sličan sa  zbog topološke zatvorenosti (uzmi neki niz koji ide u 0 ili u 1...). zbog topološke zatvorenosti (uzmi neki niz koji ide u 0 ili u 1...).
I onda se vidi da baš ova svojstva koja ''odvajaju'' ova dva skupa od  , da ih odvajaju i međusobno: jedan od njih je gust, drugi nije. , da ih odvajaju i međusobno: jedan od njih je gust, drugi nije. |
Hvala puno! Nisam se sjetila praznog skupa a očito spada jel onda odgovor je različit  , i asistenti su mi rekli da imam problema sa samopouzdanjem u vezi ovog predmeta XD.. , i asistenti su mi rekli da imam problema sa samopouzdanjem u vezi ovog predmeta XD..
|
|
| [Vrh] |
|
horaf
Forumaš(ica)

Pridružen/a: 25. 01. 2013. (19:36:39)
Postovi: (7)16
|
|
| [Vrh] |
|
|





