|
Zadatci s blica:
1) Ima li graf funkcije [latex]f:\mathbb{R} \to \mathbb{R}, f(x)=2x[/latex] povrsinu 0? A ima li mjeru 0?
2) Ima li trokut s vrhovima u tockama [latex](-1,0), (1,0), (0,1)[/latex] povrsinu? Dokazite!
3) Odredite oscilaciju funkcije
[tex]
f(x)=1[/tex] za [tex]x>0[/tex]
[tex]f(0)=2[/tex]
[tex]f(x)=-1[/tex] za [tex]x<0\\[/tex]
u svim tockama iz [tex]\mathbb{R}[/tex]
Rješenja:
1) Graf funkcije nema površinu 0, ali ima mjeru 0. Naime, graf funkcije je neograničen skup u [tex]\mathbb{R}^2[/tex], a poznato je da, kad bi imao površinu nula, trebalo bi ga se moći pokriti sa konačno pravokutnika (što govori [b]Lema 6.3[/b]. u skripti).
No, unija konačno mnogo pravokutnika je ograničen skup, a nemoguće je ograničenim skupom prekriti neograničeni skup.
No, graf te funkcije ima mjeru nula. Dapače, graf bilo koje neprekidne funkcije je skup mjere nula, taj rezultat direktno slijedi iz kombinacijom [b]Primjera 6.4.[/b] i [b]Propozicije 6.5[/b]. Naime, [tex]\mathbb{R}[/tex] možemo podijeliti u prebrojivo mnogo zatvorenih segmenata, restrikcija neprekidne funkcije je i dalje neprekidna pa je i integrabilna na tom segmentu.
[b]Primjer 6.4[/b]. nam tada daje da njen graf ima površinu 0 iz čega trivijalno slijedi da dio grafa funkcije koji odgovara jednom segmentu ima mjeru nula. Sada možemo cijeli graf prikazati kao uniju grafova restrikcija na segmente, pa nam[b] Propozicija 6.5. [/b]daje da to ima u konačnici mjeru 0.
No, za ovu funkciju se može pokazati i direktno, prekrivanjem s prebrojivo mnogo pravokutnika, slično kao što je to napravljeno u [b]Primjeru 6.6.[/b] sa skupom [tex]\mathbb{R}[/tex]
2) Taj trokut je svakako ograničen skup. Nadalje, rub tog trokuta su tri dužine za koje se, slično kao gore, može pokazati da imaju površinu nula.
(pošto su sve tri stranice tog trokuta grafovi integrabilnih funkcija na segmentima, Primjer 6.4. nam daje da su oni površine nula. Ali opet, oni su se mogli i direktno prekriti)
Dakle, imamo ograničen skup čiji rub ima površinu nula. Zaključak je da taj skup ima površinu (kao što kaže [b]Napomena 6.8[/b]., to je trivijalna posljedica Lebesgueovog teorema)
3) Oscilacija funkcije u točkama u kojima je funkcija neprekidna je nula. To znači da u većini točaka iz [tex]\mathbb{R}[/tex] zadana funkcija ima oscilacije nula. Jedini problem je dakle točka 0.
No, pošto je funkcija po dijelovima konstanta, jasno je da će u svakoj okolini, ma koliko maloj, maksimalan skok funkcije biti upravo kad njena vrijednost ide iz -1 u 2, dakle "skok" vrijednosti 3 iz čega se da zaključiti da je oscilacije funkcije u nuli jednaka 3.
Formalnije, na svakom otvorenom intervalu oko nule je
[tex]sup |f(x_1) - f(x_2)| = 3[/tex], pa je tražena oscilacija u točki nula infimum jednočlanog skupa [tex]\{3\}[/tex], dakle 3.
Zadatci s blica:
1) Ima li graf funkcije 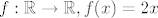 povrsinu 0? A ima li mjeru 0? povrsinu 0? A ima li mjeru 0?
2) Ima li trokut s vrhovima u tockama 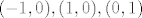 povrsinu? Dokazite! povrsinu? Dokazite!
3) Odredite oscilaciju funkcije
[tex]
f(x)=1[/tex] za [tex]x>0[/tex]
[tex]f(0)=2[/tex]
[tex]f(x)=-1[/tex] za [tex]x<0\\[/tex]
u svim tockama iz [tex]\mathbb{R}[/tex]
Rješenja:
1) Graf funkcije nema površinu 0, ali ima mjeru 0. Naime, graf funkcije je neograničen skup u [tex]\mathbb{R}^2[/tex], a poznato je da, kad bi imao površinu nula, trebalo bi ga se moći pokriti sa konačno pravokutnika (što govori Lema 6.3. u skripti).
No, unija konačno mnogo pravokutnika je ograničen skup, a nemoguće je ograničenim skupom prekriti neograničeni skup.
No, graf te funkcije ima mjeru nula. Dapače, graf bilo koje neprekidne funkcije je skup mjere nula, taj rezultat direktno slijedi iz kombinacijom Primjera 6.4. i Propozicije 6.5. Naime, [tex]\mathbb{R}[/tex] možemo podijeliti u prebrojivo mnogo zatvorenih segmenata, restrikcija neprekidne funkcije je i dalje neprekidna pa je i integrabilna na tom segmentu.
Primjer 6.4. nam tada daje da njen graf ima površinu 0 iz čega trivijalno slijedi da dio grafa funkcije koji odgovara jednom segmentu ima mjeru nula. Sada možemo cijeli graf prikazati kao uniju grafova restrikcija na segmente, pa nam Propozicija 6.5. daje da to ima u konačnici mjeru 0.
No, za ovu funkciju se može pokazati i direktno, prekrivanjem s prebrojivo mnogo pravokutnika, slično kao što je to napravljeno u Primjeru 6.6. sa skupom [tex]\mathbb{R}[/tex]
2) Taj trokut je svakako ograničen skup. Nadalje, rub tog trokuta su tri dužine za koje se, slično kao gore, može pokazati da imaju površinu nula.
(pošto su sve tri stranice tog trokuta grafovi integrabilnih funkcija na segmentima, Primjer 6.4. nam daje da su oni površine nula. Ali opet, oni su se mogli i direktno prekriti)
Dakle, imamo ograničen skup čiji rub ima površinu nula. Zaključak je da taj skup ima površinu (kao što kaže Napomena 6.8., to je trivijalna posljedica Lebesgueovog teorema)
3) Oscilacija funkcije u točkama u kojima je funkcija neprekidna je nula. To znači da u većini točaka iz [tex]\mathbb{R}[/tex] zadana funkcija ima oscilacije nula. Jedini problem je dakle točka 0.
No, pošto je funkcija po dijelovima konstanta, jasno je da će u svakoj okolini, ma koliko maloj, maksimalan skok funkcije biti upravo kad njena vrijednost ide iz -1 u 2, dakle "skok" vrijednosti 3 iz čega se da zaključiti da je oscilacije funkcije u nuli jednaka 3.
Formalnije, na svakom otvorenom intervalu oko nule je
[tex]sup |f(x_1) - f(x_2)| = 3[/tex], pa je tražena oscilacija u točki nula infimum jednočlanog skupa [tex]\{3\}[/tex], dakle 3.
|





