| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
Lafiel
Forumaš(ica)


Pridružen/a: 26. 09. 2007. (09:56:59)
Postovi: (153)16
Spol: 
|
 Postano: 20:48 čet, 11. 4. 2013 Naslov: Postano: 20:48 čet, 11. 4. 2013 Naslov: |
    |
|
|
Hvala ti, Phoenix. Da mogu, dala bih ti još 6 karma bodova. :)
[size=9][color=#999999]Added after 6 minutes:[/color][/size]
[quote="kosani"]2 pitanja:
1) 4. zadatak b) http://web.math.pmf.unizg.hr/nastava/mii/files/mi-kol1-2009-rj.pdf
Kako znamo da [tex]E \in M(R)[/tex]. Pitam jer ne razumijem kako možemo zaključiti da [tex]E \cup F_{i} \in M(R)[/tex][/quote]
Ako imaš rastući niz [tex](F_{i})[/tex] iz [tex]\mathcal{L}(E)[/tex], onda je [tex](E \cup F_{i}) \in \mathcal{M}(R)[/tex] po samoj definiciji skupa [tex]\mathcal{L}(E)[/tex], a još k tome je i rastući jer je [tex](F_{i})[/tex] rastući.
@Phoenix, nigdje nije rečeno da je [tex]E[/tex] iz [tex]\mathcal{R}[/tex], samo da je [tex]E \subseteq X[/tex]. Osim ako nekim drugim načinom nisi došao do zaključka da je iz [tex]\mathcal{R}[/tex]. Pričamo o b) dijelu zadatka. :)
Hvala ti, Phoenix. Da mogu, dala bih ti još 6 karma bodova. 
Added after 6 minutes:
Ako imaš rastući niz [tex](F_{i})[/tex] iz [tex]\mathcal{L}(E)[/tex], onda je [tex](E \cup F_{i}) \in \mathcal{M}(R)[/tex] po samoj definiciji skupa [tex]\mathcal{L}(E)[/tex], a još k tome je i rastući jer je [tex](F_{i})[/tex] rastući.
@Phoenix, nigdje nije rečeno da je [tex]E[/tex] iz [tex]\mathcal{R}[/tex], samo da je [tex]E \subseteq X[/tex]. Osim ako nekim drugim načinom nisi došao do zaključka da je iz [tex]\mathcal{R}[/tex]. Pričamo o b) dijelu zadatka. 
_________________
Weit von hier fällt Gold von den Sternen
|
|
| [Vrh] |
|
Phoenix
Forumaš(ica)


Pridružen/a: 15. 05. 2010. (18:46:07)
Postovi: (164)16
Sarma: -
|
|
| [Vrh] |
|
kosani
Forumaš(ica)
Pridružen/a: 14. 11. 2010. (21:22:58)
Postovi: (26)16
|
|
| [Vrh] |
|
Phoenix
Forumaš(ica)


Pridružen/a: 15. 05. 2010. (18:46:07)
Postovi: (164)16
Sarma: -
|
|
| [Vrh] |
|
kosani
Forumaš(ica)
Pridružen/a: 14. 11. 2010. (21:22:58)
Postovi: (26)16
|
|
| [Vrh] |
|
kobila krsto
Forumaš(ica)
Pridružen/a: 02. 07. 2009. (16:55:08)
Postovi: (6A)16
|
|
| [Vrh] |
|
Lafiel
Forumaš(ica)


Pridružen/a: 26. 09. 2007. (09:56:59)
Postovi: (153)16
Spol: 
|
|
| [Vrh] |
|
mathh5
Forumaš(ica)
Pridružen/a: 26. 05. 2012. (12:16:25)
Postovi: (E)16
|
|
| [Vrh] |
|
ddujmic
Forumaš(ica)

Pridružen/a: 17. 02. 2009. (14:01:31)
Postovi: (75)16
|
|
| [Vrh] |
|
ceps
Forumaš(ica)

Pridružen/a: 08. 10. 2010. (13:03:07)
Postovi: (13A)16
|
 Postano: 15:49 čet, 6. 6. 2013 Naslov: Postano: 15:49 čet, 6. 6. 2013 Naslov: |
    |
|
|
[quote="Lafiel"]Ovo vjerojatno više spada pod Analizu nego pod Mjeru, ali pitanjce vezano uz [url=http://web.math.pmf.unizg.hr/nastava/mii/files/kviz11.pdf]Kviz 11 c)[/url]: u kakvom su odnosu [tex]\int_0^1 (- ln x)^p\,dx[/tex] i [tex]\int_0^1 \frac{dx}{\sqrt{x}}[/tex] ? :oops:[/quote]
Pa, fora je u uspoređivanju funkcija ispod integrala.
Pomoću D'Alambertove formule možeš vidjeti da [latex]\lim_{x \to 0} \frac{-ln(x)}{\frac{1}{\sqrt{x}}} = 0[/latex] . Kad imaš to, možeš sličnom forom zaključiti isto za [latex]|ln(x)|^p[/latex]. Preko toga onda možeš ograničiti integral od logaritma integralom od korijena.
Možda netko ima neku bržu/lakšu/pametniju foru, to meni pada na pamet.
| Lafiel (napisa): | Ovo vjerojatno više spada pod Analizu nego pod Mjeru, ali pitanjce vezano uz Kviz 11 c): u kakvom su odnosu [tex]\int_0^1 (- ln x)^p\,dx[/tex] i [tex]\int_0^1 \frac{dx}{\sqrt{x}}[/tex] ?  |
Pa, fora je u uspoređivanju funkcija ispod integrala.
Pomoću D'Alambertove formule možeš vidjeti da 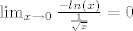 . Kad imaš to, možeš sličnom forom zaključiti isto za . Kad imaš to, možeš sličnom forom zaključiti isto za 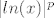 . Preko toga onda možeš ograničiti integral od logaritma integralom od korijena. . Preko toga onda možeš ograničiti integral od logaritma integralom od korijena.
Možda netko ima neku bržu/lakšu/pametniju foru, to meni pada na pamet.
|
|
| [Vrh] |
|
Gost
|
 Postano: 0:21 pet, 7. 6. 2013 Naslov: Postano: 0:21 pet, 7. 6. 2013 Naslov: |
    |
|
|
[quote="ceps"][quote="Lafiel"]Ovo vjerojatno više spada pod Analizu nego pod Mjeru, ali pitanjce vezano uz [url=http://web.math.pmf.unizg.hr/nastava/mii/files/kviz11.pdf]Kviz 11 c)[/url]: u kakvom su odnosu [tex]\int_0^1 (- ln x)^p\,dx[/tex] i [tex]\int_0^1 \frac{dx}{\sqrt{x}}[/tex] ? :oops:[/quote]
Pa, fora je u uspoređivanju funkcija ispod integrala.
Pomoću D'Alambertove formule možeš vidjeti da [latex]\lim_{x \to 0} \frac{-ln(x)}{\frac{1}{\sqrt{x}}} = 0[/latex] . Kad imaš to, možeš sličnom forom zaključiti isto za [latex]|ln(x)|^p[/latex]. Preko toga onda možeš ograničiti integral od logaritma integralom od korijena.
Možda netko ima neku bržu/lakšu/pametniju foru, to meni pada na pamet.[/quote]
Mozes li ovo detaljnije raspisati? Trazio sam formulu o kojoj pricas no nisam ju nasao.
Hvala
| ceps (napisa): | | Lafiel (napisa): | Ovo vjerojatno više spada pod Analizu nego pod Mjeru, ali pitanjce vezano uz Kviz 11 c): u kakvom su odnosu [tex]\int_0^1 (- ln x)^p\,dx[/tex] i [tex]\int_0^1 \frac{dx}{\sqrt{x}}[/tex] ?  |
Pa, fora je u uspoređivanju funkcija ispod integrala.
Pomoću D'Alambertove formule možeš vidjeti da 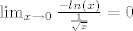 . Kad imaš to, možeš sličnom forom zaključiti isto za . Kad imaš to, možeš sličnom forom zaključiti isto za 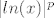 . Preko toga onda možeš ograničiti integral od logaritma integralom od korijena. . Preko toga onda možeš ograničiti integral od logaritma integralom od korijena.
Možda netko ima neku bržu/lakšu/pametniju foru, to meni pada na pamet. |
Mozes li ovo detaljnije raspisati? Trazio sam formulu o kojoj pricas no nisam ju nasao.
Hvala
|
|
| [Vrh] |
|
Lafiel
Forumaš(ica)


Pridružen/a: 26. 09. 2007. (09:56:59)
Postovi: (153)16
Spol: 
|
|
| [Vrh] |
|
Gost
|
 Postano: 22:22 pon, 17. 6. 2013 Naslov: Postano: 22:22 pon, 17. 6. 2013 Naslov: |
    |
|
|
Da konvergira prema f se vidi lako iz definicije:
1) ako je f(x) = +beskonacno onda je fn(x) = n pa je sad ocito
2) ako je f(x) konacan, onda ce se za dovoljno veliki n, fn(x) razlikovati od f(x) za 1/2^n (vidi se iz definicije A(n,k)) pa ocito konvergira prema f(x)
Da raste: ako je f(x) = +beskonacno, onda je fn(x) = n pa ocito raste.
Neka je f(x) konacan. Neka je (najvece cijelo od f(x)) = m. Tada za n<m je fn(x) = n pa ocito raste. Neka je sada n>=m proizvoljan, tada po definiciji od fn(x) postoji k takav da
(k-1)/2^n <= f(x) < k/2^n
pa je
fn(x) = (k-1)/2^n ; posebno fn(x)=(2k-2)/2^(n+1)
sada ocito f(n+1)(x) moze biti po definiciji:
(2k-2)/2^(n+1) ili (2k-1)/2^(n+1),
jer je f(x) iz
(2k-2)/2^(n+1) <= f(x) < (2k-1)/2^(n+1)
ili
(2k-1)/2^(n+1) <= f(x) < (2k)/2^(n+1)
Zao mi je sto nije u latexu :oops:
Da konvergira prema f se vidi lako iz definicije:
1) ako je f(x) = +beskonacno onda je fn(x) = n pa je sad ocito
2) ako je f(x) konacan, onda ce se za dovoljno veliki n, fn(x) razlikovati od f(x) za 1/2^n (vidi se iz definicije A(n,k)) pa ocito konvergira prema f(x)
Da raste: ako je f(x) = +beskonacno, onda je fn(x) = n pa ocito raste.
Neka je f(x) konacan. Neka je (najvece cijelo od f(x)) = m. Tada za n<m je fn(x) = n pa ocito raste. Neka je sada n>=m proizvoljan, tada po definiciji od fn(x) postoji k takav da
(k-1)/2^n <= f(x) < k/2^n
pa je
fn(x) = (k-1)/2^n ; posebno fn(x)=(2k-2)/2^(n+1)
sada ocito f(n+1)(x) moze biti po definiciji:
(2k-2)/2^(n+1) ili (2k-1)/2^(n+1),
jer je f(x) iz
(2k-2)/2^(n+1) <= f(x) < (2k-1)/2^(n+1)
ili
(2k-1)/2^(n+1) <= f(x) < (2k)/2^(n+1)
Zao mi je sto nije u latexu 
|
|
| [Vrh] |
|
Phoenix
Forumaš(ica)


Pridružen/a: 15. 05. 2010. (18:46:07)
Postovi: (164)16
Sarma: -
|
 Postano: 22:53 pon, 17. 6. 2013 Naslov: Postano: 22:53 pon, 17. 6. 2013 Naslov: |
    |
|
|
Da, pogotovo kada se u kolokviju vjerojatno nije smjelo "lako vidjeti"... :)
Možda ne bi bilo loše znati otprilike kako točno funkcije [tex]f_n[/tex] opisuju funkciju [tex]f[/tex]. :)
OK, za neki [tex]n[/tex] funkcija [tex]f_n[/tex] je jednostavna funkcija i poprima vrijednosti iz skupa [tex]\left\{ 0, \frac{1}{2^n}, ..., \frac{n \cdot 2^n-1}{2^n}, \frac{n \cdot 2^n}{2^n} = n \right\}[/tex] i to na sljedeći način: ako je (za neki [tex]x \in X[/tex]) vrijednost [tex]f(x)[/tex] u segmentu [tex]\left[ \frac{k-1}{2^n}, \frac{k}{2^n} \right>[/tex], tada je [tex]f_n(x)=\frac{k-1}{2^n}[/tex]. (I, dodatno, ako je [tex]f(x)\geq n[/tex], tada je jednostavno [tex]f_n(x)=n[/tex].)
Evo primjer kako otprilike izgleda funkcija [tex]f_n[/tex] za neku [tex]f[/tex] koja je nalik krivulji polinoma trećeg stupnja:
[img]http://i43.tinypic.com/357hd77.png[/img]
Dakle, ova valovita krivulja neka je promatrana funkcija [tex]f[/tex], ove svjetloplave crte neka označavaju vrijednosti oblika [tex]\frac{k}{2^n}[/tex]. Tada tamnoplave crte zajedno predstavljaju graf funkcije [tex]f_n[/tex]!
Sada, prijelaz na [tex]f_{n+1}[/tex]... Direktno iz definicije, ta funkcija postiže vrijednosti [tex]0, \frac{1}{2^{n+1}}, \frac{2}{2^{n+1}}=\frac{1}{2^n}, \frac{3}{2^{n+1}}, \frac{4}{2^{n+1}}=\frac{2}{2^n}, ..., \frac{(n+1) \cdot 2^{n+1}-1}{2^{n+1}}, \frac{(n+1) \cdot 2^{n+1}}{2^{n+1}}=n+1[/tex]. Odnosno, u odnosu na prethodnu [tex]f_n[/tex], između svake dvije svjetloplave crte nadodaješ još jednu svjetloplavu crtu (kao i između one najdonje te [tex]x[/tex] osi :) ), a onda između [tex]n[/tex] i [tex]n+1[/tex] dodaš onoliko jednako udaljenih svjetloplavih crta koliko je potrebno (da mreža bude podjednaka). I dobivaš sljedeće:
[img]http://i39.tinypic.com/fbj6sh.png[/img]
Sada je nekako jasnije da ovaj niz funkcija poprilično dobro opisuje početnu funkciju [tex]f[/tex]. :)
A sada, vezano uz tvoje pitanje, uoči na ovim dvijema skicama sljedeće: pri prijelazu s jedne slike na drugu, određeni komad tamnoplave linije ili ostaje na istom mjestu ili se podiže, i to za točno [tex]\frac{1}{2^{n+1}}[/tex].
Ovo zapažanje ti pomaže da argumentiraš monotonost i konvergenciju niza funkcija i to na sljedeći način:
- Za [tex]x \in X[/tex] i [tex]n \in \mathbb{N}[/tex] postoji [tex]k \in \mathbb{N}[/tex] takav da je [tex]\frac{k-1}{2^n} \leq f(x) < \frac{k}{2^n}[/tex], iz čega onda slijedi [tex]f_n(x)=\frac{k-1}{2^n}[/tex]. Ovisno o tome je li [tex]f(x)<\frac{2k-1}{2^{n+1}}[/tex] ili [tex]f(x) \geq \frac{2k-1}{2^{n+1}}[/tex], slijedi da je [tex]f_{n+1}(x)=\frac{k-1}{2^n}[/tex] ili [tex]f_{n+1}(x)=\frac{2k-1}{2^{n+1}}[/tex]. U svakom slučaju je [tex]f_n(x) \leq f_{n+1}(x)[/tex]. Slična argumentacija slijedi i za [tex]f(x) \geq n[/tex] (čisto zbog formalnosti drugačiji slučaj).
- U slučaju [tex]f(x)<+\infty[/tex] (inače je [tex]f_n(x)=n \stackrel{n \rightarrow +\infty}{\longrightarrow} +\infty[/tex]) postoji dovoljno veliki [tex]n \in \mathbb{N}[/tex] takav da je [tex]n \leq f(x) < n+1[/tex]. Po definiciji od [tex]f_n[/tex] je tada [tex]0 \leq f(x)-f_n(x) \leq \frac{1}{2^{n+1}} \stackrel{n \rightarrow +\infty}{\longrightarrow} 0[/tex]. Iz ovoga slijedi [tex]\lim \limits_{n \rightarrow +\infty}f_n(x) = f(x), \forall x \in X[/tex].
Evo, ovo je moj komentar na teorem, zapravo slično onome što je kolega Gost već napisao. :)
U principu, po meni je najbitnije imati u glavi ove skice (koje su mogle biti i bolje i detaljnije, ali eto, znam crtati samo u Paintu i nemam skener :D ) i onda praktički znaš "pjevati" dokaz (nemaš problema niti s definicijom skupova [tex]A_n[/tex]). ;)
Da, pogotovo kada se u kolokviju vjerojatno nije smjelo "lako vidjeti"... 
Možda ne bi bilo loše znati otprilike kako točno funkcije [tex]f_n[/tex] opisuju funkciju [tex]f[/tex]. 
OK, za neki [tex]n[/tex] funkcija [tex]f_n[/tex] je jednostavna funkcija i poprima vrijednosti iz skupa [tex]\left\{ 0, \frac{1}{2^n}, ..., \frac{n \cdot 2^n-1}{2^n}, \frac{n \cdot 2^n}{2^n} = n \right\}[/tex] i to na sljedeći način: ako je (za neki [tex]x \in X[/tex]) vrijednost [tex]f(x)[/tex] u segmentu [tex]\left[ \frac{k-1}{2^n}, \frac{k}{2^n} \right>[/tex], tada je [tex]f_n(x)=\frac{k-1}{2^n}[/tex]. (I, dodatno, ako je [tex]f(x)\geq n[/tex], tada je jednostavno [tex]f_n(x)=n[/tex].)
Evo primjer kako otprilike izgleda funkcija [tex]f_n[/tex] za neku [tex]f[/tex] koja je nalik krivulji polinoma trećeg stupnja:

Dakle, ova valovita krivulja neka je promatrana funkcija [tex]f[/tex], ove svjetloplave crte neka označavaju vrijednosti oblika [tex]\frac{k}{2^n}[/tex]. Tada tamnoplave crte zajedno predstavljaju graf funkcije [tex]f_n[/tex]!
Sada, prijelaz na [tex]f_{n+1}[/tex]... Direktno iz definicije, ta funkcija postiže vrijednosti [tex]0, \frac{1}{2^{n+1}}, \frac{2}{2^{n+1}}=\frac{1}{2^n}, \frac{3}{2^{n+1}}, \frac{4}{2^{n+1}}=\frac{2}{2^n}, ..., \frac{(n+1) \cdot 2^{n+1}-1}{2^{n+1}}, \frac{(n+1) \cdot 2^{n+1}}{2^{n+1}}=n+1[/tex]. Odnosno, u odnosu na prethodnu [tex]f_n[/tex], između svake dvije svjetloplave crte nadodaješ još jednu svjetloplavu crtu (kao i između one najdonje te [tex]x[/tex] osi  ), a onda između [tex]n[/tex] i [tex]n+1[/tex] dodaš onoliko jednako udaljenih svjetloplavih crta koliko je potrebno (da mreža bude podjednaka). I dobivaš sljedeće: ), a onda između [tex]n[/tex] i [tex]n+1[/tex] dodaš onoliko jednako udaljenih svjetloplavih crta koliko je potrebno (da mreža bude podjednaka). I dobivaš sljedeće:

Sada je nekako jasnije da ovaj niz funkcija poprilično dobro opisuje početnu funkciju [tex]f[/tex]. 
A sada, vezano uz tvoje pitanje, uoči na ovim dvijema skicama sljedeće: pri prijelazu s jedne slike na drugu, određeni komad tamnoplave linije ili ostaje na istom mjestu ili se podiže, i to za točno [tex]\frac{1}{2^{n+1}}[/tex].
Ovo zapažanje ti pomaže da argumentiraš monotonost i konvergenciju niza funkcija i to na sljedeći način:
- Za [tex]x \in X[/tex] i [tex]n \in \mathbb{N}[/tex] postoji [tex]k \in \mathbb{N}[/tex] takav da je [tex]\frac{k-1}{2^n} \leq f(x) < \frac{k}{2^n}[/tex], iz čega onda slijedi [tex]f_n(x)=\frac{k-1}{2^n}[/tex]. Ovisno o tome je li [tex]f(x)<\frac{2k-1}{2^{n+1}}[/tex] ili [tex]f(x) \geq \frac{2k-1}{2^{n+1}}[/tex], slijedi da je [tex]f_{n+1}(x)=\frac{k-1}{2^n}[/tex] ili [tex]f_{n+1}(x)=\frac{2k-1}{2^{n+1}}[/tex]. U svakom slučaju je [tex]f_n(x) \leq f_{n+1}(x)[/tex]. Slična argumentacija slijedi i za [tex]f(x) \geq n[/tex] (čisto zbog formalnosti drugačiji slučaj).
- U slučaju [tex]f(x)<+\infty[/tex] (inače je [tex]f_n(x)=n \stackrel{n \rightarrow +\infty}{\longrightarrow} +\infty[/tex]) postoji dovoljno veliki [tex]n \in \mathbb{N}[/tex] takav da je [tex]n \leq f(x) < n+1[/tex]. Po definiciji od [tex]f_n[/tex] je tada [tex]0 \leq f(x)-f_n(x) \leq \frac{1}{2^{n+1}} \stackrel{n \rightarrow +\infty}{\longrightarrow} 0[/tex]. Iz ovoga slijedi [tex]\lim \limits_{n \rightarrow +\infty}f_n(x) = f(x), \forall x \in X[/tex].
Evo, ovo je moj komentar na teorem, zapravo slično onome što je kolega Gost već napisao. 
U principu, po meni je najbitnije imati u glavi ove skice (koje su mogle biti i bolje i detaljnije, ali eto, znam crtati samo u Paintu i nemam skener  ) i onda praktički znaš "pjevati" dokaz (nemaš problema niti s definicijom skupova [tex]A_n[/tex]). ) i onda praktički znaš "pjevati" dokaz (nemaš problema niti s definicijom skupova [tex]A_n[/tex]). 
|
|
| [Vrh] |
|
Lafiel
Forumaš(ica)


Pridružen/a: 26. 09. 2007. (09:56:59)
Postovi: (153)16
Spol: 
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
Lafiel
Forumaš(ica)


Pridružen/a: 26. 09. 2007. (09:56:59)
Postovi: (153)16
Spol: 
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
Lafiel
Forumaš(ica)


Pridružen/a: 26. 09. 2007. (09:56:59)
Postovi: (153)16
Spol: 
|
|
| [Vrh] |
|
|










