|
Dosta dobro pitanje, no mislim da niti jedna od opcija koju si navela nije pravi odgovor :) .
Mislim da pravi odgovor leži u pristupu matematici, posebno, pristupu ovom studiju. Prvo, mislim da je specifičnost ovog to što su kolegiji koje slušamo međusobno povezani, nadovezuju se jedni na druge i nema smisla promatrati ih kao odvojene cjeline ("Sad sam položio/la Matematičku analizu 2, mogu je zaboraviti jer ćemo na Kompleksnoj analizi raditi nešto potpuno stoto."). Osobno smatram da je ideja studija najprije na nižim godinama naučiti neke osnovne pojmove i koncepte u matematici kako bismo kasnije detaljnije mogli proučavati neka specifična područja (ovisno o tome na kojem smo konkretnom studiju). Konkretno, u ovom kolegiju je za rješavanje određenih zadataka potrebno i neko elementarno znanje matematičke analize (one koja se uči na 1. godini oba studija) - nemam dojam da je to nešto što bi itko trebao očekivati da će naučiti na ovom kolegiju, to je nešto što se podrazumijeva da shvaćate s prijašnjih godina (kao neko bazično znanje potrebno za shvaćanje bilo kakve matematike).
Drugo, ovaj kolegij (po mom osobnom mišljenju) ne obrađuje neke kompleksne matematičke koncepte, već bi nas trebao upoznati s osnovnim pojmovima potrebnim za proučavanje ikakve složenije matematičke teorije. Koliko god se nekima ovaj kolegij činio zahtjevnim za polaganje, samo gradivo kolegija nije teško, već bazično (kao da učite osnovne fraze i riječi nekog stranog jezika kako biste kasnije mogli naučiti gramatiku, sporazumijevati se...). Zato nije niti čudno što se u kolegiju pojavljuju sadržaji i iz nekih drugih područja matematike - razumijevanje ovakvih definicija i osnovnih rezultata kolegija najlakše je provjeriti na nekim konkretnim primjerima (a i najsmislenije - ovdje nije riječ o visoko apstraktnim konceptima, već o pojmovima koji se naveliko koriste u raznim područjima matematike - zato i ima smisla vidjeti kako te stvari izgledaju u nekom konkretnom metričkom/topološkom prostoru).
Treće, bit matematike (barem po meni) nije prolaženje mnogobrojnih specifičnih primjera, bit je u shvaćanju i razumijevanju ideja. I Lucija, i ja smo vam na demonstraturama vrlo često znali postavljati razna pitanja kako bismo ukazali na ključne korake dokaza i moguća poopćenja zadataka koje smo rješavali, prethodna je rečenica razlog tome. Vi možete naučiti rješavati 550 različitih vrsta zadataka a da i dalje ne razumijete gradivo koje se obrađuje - to će u nekim slučajevima možda biti i dovoljno kako biste položili kolegij, ali svakako ne i da možete tvrditi kako znate neki dio matematike (usput rečeno, takav, po meni, krivi pristup je, između ostaloga, i razlog zašto naši učenici u osnovnim i srednjim školama imaju problema s matematikom). Po meni je bit i poanta ovog kolegija da u idućim matematičkim kolegijima razumijemo matematičke koncepte vezane uz ove pojmove (npr., da svi razumijemo što znači da je funkcija klase [latex]C^{\infty}_c(\mathbb{R})[/latex], da je [i]lokalno integrabilna[/i], da red funkcija konvergira [i]lokalno uniformno[/i], da znamo da u [i]području[/i] [latex]\Omega[/latex] neki pravi neprazan podskup od [latex]\Omega[/latex] ne može biti istovremeno otvoren i zatvoren, da neki niz može konvergirati u različitim normama/metrikama, ...) i da pri budućem spominjanju tih pojmova u npr. pretpostavkama teorema nemamo problema s njihovim shvaćanjem.
Tako da, "učiti pecati" u ovom kolegiju je dosta teško jer "pecati" zapravo znači razumijevati koncepte koji su obrađeni u prijašnjim kolegijima.
Nadam se da ovo barem dijelom odgovara na pitanje,
Kristijan
P.S. Ovim kratkim elaboratom mi nije namjera nikoga vrijeđati niti omalovažavati, samo iznosim svoje stavove. Također, sve što sam naveo govorim u svoje ime (dakle, niti u Lucijino, niti u ime bilo kojeg drugog od mojih kolega ili profesora/asistenata) i ovo je sve moj osobni stav :D
Dosta dobro pitanje, no mislim da niti jedna od opcija koju si navela nije pravi odgovor  . .
Mislim da pravi odgovor leži u pristupu matematici, posebno, pristupu ovom studiju. Prvo, mislim da je specifičnost ovog to što su kolegiji koje slušamo međusobno povezani, nadovezuju se jedni na druge i nema smisla promatrati ih kao odvojene cjeline ("Sad sam položio/la Matematičku analizu 2, mogu je zaboraviti jer ćemo na Kompleksnoj analizi raditi nešto potpuno stoto."). Osobno smatram da je ideja studija najprije na nižim godinama naučiti neke osnovne pojmove i koncepte u matematici kako bismo kasnije detaljnije mogli proučavati neka specifična područja (ovisno o tome na kojem smo konkretnom studiju). Konkretno, u ovom kolegiju je za rješavanje određenih zadataka potrebno i neko elementarno znanje matematičke analize (one koja se uči na 1. godini oba studija) - nemam dojam da je to nešto što bi itko trebao očekivati da će naučiti na ovom kolegiju, to je nešto što se podrazumijeva da shvaćate s prijašnjih godina (kao neko bazično znanje potrebno za shvaćanje bilo kakve matematike).
Drugo, ovaj kolegij (po mom osobnom mišljenju) ne obrađuje neke kompleksne matematičke koncepte, već bi nas trebao upoznati s osnovnim pojmovima potrebnim za proučavanje ikakve složenije matematičke teorije. Koliko god se nekima ovaj kolegij činio zahtjevnim za polaganje, samo gradivo kolegija nije teško, već bazično (kao da učite osnovne fraze i riječi nekog stranog jezika kako biste kasnije mogli naučiti gramatiku, sporazumijevati se...). Zato nije niti čudno što se u kolegiju pojavljuju sadržaji i iz nekih drugih područja matematike - razumijevanje ovakvih definicija i osnovnih rezultata kolegija najlakše je provjeriti na nekim konkretnim primjerima (a i najsmislenije - ovdje nije riječ o visoko apstraktnim konceptima, već o pojmovima koji se naveliko koriste u raznim područjima matematike - zato i ima smisla vidjeti kako te stvari izgledaju u nekom konkretnom metričkom/topološkom prostoru).
Treće, bit matematike (barem po meni) nije prolaženje mnogobrojnih specifičnih primjera, bit je u shvaćanju i razumijevanju ideja. I Lucija, i ja smo vam na demonstraturama vrlo često znali postavljati razna pitanja kako bismo ukazali na ključne korake dokaza i moguća poopćenja zadataka koje smo rješavali, prethodna je rečenica razlog tome. Vi možete naučiti rješavati 550 različitih vrsta zadataka a da i dalje ne razumijete gradivo koje se obrađuje - to će u nekim slučajevima možda biti i dovoljno kako biste položili kolegij, ali svakako ne i da možete tvrditi kako znate neki dio matematike (usput rečeno, takav, po meni, krivi pristup je, između ostaloga, i razlog zašto naši učenici u osnovnim i srednjim školama imaju problema s matematikom). Po meni je bit i poanta ovog kolegija da u idućim matematičkim kolegijima razumijemo matematičke koncepte vezane uz ove pojmove (npr., da svi razumijemo što znači da je funkcija klase 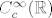 , da je lokalno integrabilna, da red funkcija konvergira lokalno uniformno, da znamo da u području , da je lokalno integrabilna, da red funkcija konvergira lokalno uniformno, da znamo da u području 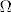 neki pravi neprazan podskup od neki pravi neprazan podskup od 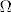 ne može biti istovremeno otvoren i zatvoren, da neki niz može konvergirati u različitim normama/metrikama, ...) i da pri budućem spominjanju tih pojmova u npr. pretpostavkama teorema nemamo problema s njihovim shvaćanjem. ne može biti istovremeno otvoren i zatvoren, da neki niz može konvergirati u različitim normama/metrikama, ...) i da pri budućem spominjanju tih pojmova u npr. pretpostavkama teorema nemamo problema s njihovim shvaćanjem.
Tako da, "učiti pecati" u ovom kolegiju je dosta teško jer "pecati" zapravo znači razumijevati koncepte koji su obrađeni u prijašnjim kolegijima.
Nadam se da ovo barem dijelom odgovara na pitanje,
Kristijan
P.S. Ovim kratkim elaboratom mi nije namjera nikoga vrijeđati niti omalovažavati, samo iznosim svoje stavove. Također, sve što sam naveo govorim u svoje ime (dakle, niti u Lucijino, niti u ime bilo kojeg drugog od mojih kolega ili profesora/asistenata) i ovo je sve moj osobni stav 
|





