| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
Mala_022
Forumaš(ica)
Pridružen/a: 21. 01. 2006. (18:15:12)
Postovi: (73)16
Spol: 
Lokacija: ...evo mene među moje...
|
 Postano: 22:00 sri, 11. 5. 2016 Naslov: Dva limesa Postano: 22:00 sri, 11. 5. 2016 Naslov: Dva limesa |
    |
|
|
Pozdrav svima!
Nakon godina neaktivnosti na Forumu, evo me nazad po pomoć [size=4](long live DeGiorgi)[/size] ;-D
Naišla san na dva zadatka s limesima, a s obziron na to da mi je u međuvrimenu malo zakržlja mozak, zamolila bi koji hint od vas kojima je još friško :pray:
1. Neka je [latex]L=\lim_{n \to \infty}\sqrt[n]{\prod_{i=1}^{n}(x+\dfrac{1}{2^i})}-x[/latex], odredi [latex]\lim_{n \to \infty}(nL)[/latex].
Rješenje bi kao tribalo ispasti 1. Ja san ga uspila odozgo ograničiti s 1 koristeći A-G nejednakost, ali za donju granicu mi ništa upotrebljivo ne pada na pamet (tj. sve čega se sitin ima limes u 0, a to mi ne pomaže puno). Tin više mi je sumnjivo šta za različite x-eve dobijen različit limes. Ko je tu lud?
2. Izračunaj [latex]\lim_{n \to \infty}\dfrac{1}{4^n}{\sum_{r=1}^{2^{n-1}-1}\tan^2\left(\dfrac{r\pi}{2^n}\right)[/latex].
Za ovo san imala hrpu ideja koje me nisu odvele nigdi. Sigurna san da je nešto preočito, ali ja ne vidin :neznam:
Pozdrav svima!
Nakon godina neaktivnosti na Forumu, evo me nazad po pomoć (long live DeGiorgi) 
Naišla san na dva zadatka s limesima, a s obziron na to da mi je u međuvrimenu malo zakržlja mozak, zamolila bi koji hint od vas kojima je još friško 
1. Neka je 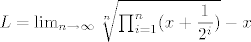 , odredi , odredi 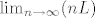 . .
Rješenje bi kao tribalo ispasti 1. Ja san ga uspila odozgo ograničiti s 1 koristeći A-G nejednakost, ali za donju granicu mi ništa upotrebljivo ne pada na pamet (tj. sve čega se sitin ima limes u 0, a to mi ne pomaže puno). Tin više mi je sumnjivo šta za različite x-eve dobijen različit limes. Ko je tu lud?
2. Izračunaj 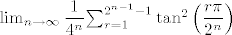 . .
Za ovo san imala hrpu ideja koje me nisu odvele nigdi. Sigurna san da je nešto preočito, ali ja ne vidin 
|
|
| [Vrh] |
|
ljpalle
Forumaš(ica)

Pridružen/a: 24. 09. 2011. (10:10:43)
Postovi: (22)16
|
 Postano: 23:20 sri, 18. 5. 2016 Naslov: Postano: 23:20 sri, 18. 5. 2016 Naslov: |
    |
|
|
1. Zadatak - Ovdje ocito valja pretpostaviti da je [tex]x > 0[/tex]. Slucaj [tex]x = 0[/tex] je lagan.
Primijetimo da niz mozemo napisati u obliku
[dtex]
L_n (x) = n x \Big( \Big(\prod_{i=1}^{n} (1 + \frac{2^{-i}}{x}) \Big )^{1/n} - 1 \Big).
[/dtex]
i sada standardnim 'trikom' s logaritmom napisemo u obliku
[dtex]
L_n (x) = x \frac{ \exp \Big( \frac{1}{n} \sum_{i=1}^{n} \ln( 1 + \frac{2^{-i}}{x} ) \Big ) - 1 }{ 1/n }.
[/dtex]
Oznacimo niz [tex]S_n (x) = \sum_{i=1}^{n} \ln( 1 + \frac{2^{-i}}{x} ) [/tex] i primijetimo da on konvergira k nekom pozitivnom broju S(x). Sada mozemo zapisati
[dtex]
L_n (x) = x S_n (x) \frac{ \exp \Big( \frac{1}{n} S_n (x) \Big ) - 1 }{ \frac{1}{n} S_n (x) }.
[/dtex]
Iz ovog je sada ocito da je [tex]L(x) = \lim_n L_n(x) = x S(x)[/tex]. Pretpostavljam da se nije mislilo u rjesenju da je [tex]L(x) = 1[/tex] nego vec [tex]\lim_{x \to \infty} L(x) = 1[/tex]. Naime, primijetimo da je
[dtex]
L(x) = \sum_{i=1}^{\infty} \ln( 1 + \frac{2^{-i}}{x} )^{ \Large x}
[/dtex]
te
[dtex]
\lim_{x \to \infty} \ln( 1 + \frac{2^{-i}}{x} )^{ \Large x} = 2^{-i}.
[/dtex]
Iz teorema o dominiranoj konvergenciji mozemo uci s limesom pod sumu pa dobijemo da je [tex]\lim_{x \to \infty} L(x) = \sum_{i=1}^{\infty} 2^{-i} = 1[/tex].
2.Zadatak
Definirajmo funkciju [tex]f(x) = \tan^2 ( \frac{\pi}{2} x )[/tex] i preuredimo dani niz na sljedeci nacin.
[dtex]
L_n = \frac{1}{2^{n+1}} \frac{1}{2^{n-1}} \sum_{r=0}^{2^{n-1}-1} f( \frac{r}{2^{n-1}} )
[/dtex]
Vidimo da je [tex]S_n = \frac{1}{2^{n-1}} \sum_{r=0}^{2^{n-1}-1} f( \frac{r}{2^{n-1}} )[/tex] zapravo gornja medja za Riemannov integral funkcije f na intervalu [tex][0,1 - \frac{1}{2^{n-1}}][/tex] i slicno se moze dobiti donja medja na integral funkcije. Na zalost, ovim razmatranjima nije moguce, koliko se meni cini, na laki nacin dobiti konkretan iznos limesa i nije mi pao na pamet bolji nacin rjesavanja ovog zadatka. Malim racunom se moze dobiti ocjena da je limes u intervalu [tex][\pi^{-2}, 2 \pi^{-2}][/tex], a ako se uzme u obzir konveksnost funkcije [tex]f[/tex], dobije se i bolja ocjena da je limes u intervalu [tex] [\frac{3}{2} \pi^{-2}, 2 \pi^{-2}][/tex].
1. Zadatak - Ovdje ocito valja pretpostaviti da je [tex]x > 0[/tex]. Slucaj [tex]x = 0[/tex] je lagan.
Primijetimo da niz mozemo napisati u obliku
[dtex]
L_n (x) = n x \Big( \Big(\prod_{i=1}^{n} (1 + \frac{2^{-i}}{x}) \Big )^{1/n} - 1 \Big).
[/dtex]
i sada standardnim 'trikom' s logaritmom napisemo u obliku
[dtex]
L_n (x) = x \frac{ \exp \Big( \frac{1}{n} \sum_{i=1}^{n} \ln( 1 + \frac{2^{-i}}{x} ) \Big ) - 1 }{ 1/n }.
[/dtex]
Oznacimo niz [tex]S_n (x) = \sum_{i=1}^{n} \ln( 1 + \frac{2^{-i}}{x} ) [/tex] i primijetimo da on konvergira k nekom pozitivnom broju S(x). Sada mozemo zapisati
[dtex]
L_n (x) = x S_n (x) \frac{ \exp \Big( \frac{1}{n} S_n (x) \Big ) - 1 }{ \frac{1}{n} S_n (x) }.
[/dtex]
Iz ovog je sada ocito da je [tex]L(x) = \lim_n L_n(x) = x S(x)[/tex]. Pretpostavljam da se nije mislilo u rjesenju da je [tex]L(x) = 1[/tex] nego vec [tex]\lim_{x \to \infty} L(x) = 1[/tex]. Naime, primijetimo da je
[dtex]
L(x) = \sum_{i=1}^{\infty} \ln( 1 + \frac{2^{-i}}{x} )^{ \Large x}
[/dtex]
te
[dtex]
\lim_{x \to \infty} \ln( 1 + \frac{2^{-i}}{x} )^{ \Large x} = 2^{-i}.
[/dtex]
Iz teorema o dominiranoj konvergenciji mozemo uci s limesom pod sumu pa dobijemo da je [tex]\lim_{x \to \infty} L(x) = \sum_{i=1}^{\infty} 2^{-i} = 1[/tex].
2.Zadatak
Definirajmo funkciju [tex]f(x) = \tan^2 ( \frac{\pi}{2} x )[/tex] i preuredimo dani niz na sljedeci nacin.
[dtex]
L_n = \frac{1}{2^{n+1}} \frac{1}{2^{n-1}} \sum_{r=0}^{2^{n-1}-1} f( \frac{r}{2^{n-1}} )
[/dtex]
Vidimo da je [tex]S_n = \frac{1}{2^{n-1}} \sum_{r=0}^{2^{n-1}-1} f( \frac{r}{2^{n-1}} )[/tex] zapravo gornja medja za Riemannov integral funkcije f na intervalu [tex][0,1 - \frac{1}{2^{n-1}}][/tex] i slicno se moze dobiti donja medja na integral funkcije. Na zalost, ovim razmatranjima nije moguce, koliko se meni cini, na laki nacin dobiti konkretan iznos limesa i nije mi pao na pamet bolji nacin rjesavanja ovog zadatka. Malim racunom se moze dobiti ocjena da je limes u intervalu [tex][\pi^{-2}, 2 \pi^{-2}][/tex], a ako se uzme u obzir konveksnost funkcije [tex]f[/tex], dobije se i bolja ocjena da je limes u intervalu [tex] [\frac{3}{2} \pi^{-2}, 2 \pi^{-2}][/tex].
|
|
| [Vrh] |
|
Mala_022
Forumaš(ica)
Pridružen/a: 21. 01. 2006. (18:15:12)
Postovi: (73)16
Spol: 
Lokacija: ...evo mene među moje...
|
 Postano: 15:05 čet, 19. 5. 2016 Naslov: Postano: 15:05 čet, 19. 5. 2016 Naslov: |
    |
|
|
[quote="ljpalle"]1. Zadatak
Pretpostavljam da se nije mislilo u rjesenju da je [tex]L(x) = 1[/tex] nego vec [tex]\lim_{x \to \infty} L(x) = 1[/tex]. [/quote]
Mislilo se da je [latex]\lim_{n \to \infty}(n \cdot L)=1[/latex] (bar san ja tako svatila rješenja).
[quote="ljpalle"]2.Zadatak
Malim racunom se moze dobiti ocjena da je limes u intervalu [tex][\pi^{-2}, 2 \pi^{-2}][/tex], a ako se uzme u obzir konveksnost funkcije [tex]f[/tex], dobije se i bolja ocjena da je limes u intervalu [tex] [\frac{3}{2} \pi^{-2}, 2 \pi^{-2}][/tex].[/quote]
Tu čak nisu ponuđeni točni odgovori, nego se traži zbroj brojnika i nazivnika do kraja skraćenog razlomka koji se dobije kao rješenje. Točan odgovor je navodno 7 (a uvrštavanjem dovoljno velikih brojeva u Wolfram alphu mogu naslutiti da bi rješenje bilo [latex]\dfrac16[/latex], šta bi odgovaralo tom kao točnom odgovoru). Jedino bi još bilo super to stvarno i moći izračunati.
U svakom slučaju, puuuuuuuuuuno hvala :thankyou: :karma:
[size=4]P.S. Drago mi je da ipak nije ispalo da san tolko zakržljala da ne vidin nešto totalno očito[/size] :mrgreen:
| ljpalle (napisa): | 1. Zadatak
Pretpostavljam da se nije mislilo u rjesenju da je [tex]L(x) = 1[/tex] nego vec [tex]\lim_{x \to \infty} L(x) = 1[/tex]. |
Mislilo se da je 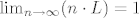 (bar san ja tako svatila rješenja). (bar san ja tako svatila rješenja).
| ljpalle (napisa): | 2.Zadatak
Malim racunom se moze dobiti ocjena da je limes u intervalu [tex][\pi^{-2}, 2 \pi^{-2}][/tex], a ako se uzme u obzir konveksnost funkcije [tex]f[/tex], dobije se i bolja ocjena da je limes u intervalu [tex] [\frac{3}{2} \pi^{-2}, 2 \pi^{-2}][/tex]. |
Tu čak nisu ponuđeni točni odgovori, nego se traži zbroj brojnika i nazivnika do kraja skraćenog razlomka koji se dobije kao rješenje. Točan odgovor je navodno 7 (a uvrštavanjem dovoljno velikih brojeva u Wolfram alphu mogu naslutiti da bi rješenje bilo  , šta bi odgovaralo tom kao točnom odgovoru). Jedino bi još bilo super to stvarno i moći izračunati. , šta bi odgovaralo tom kao točnom odgovoru). Jedino bi još bilo super to stvarno i moći izračunati.
U svakom slučaju, puuuuuuuuuuno hvala  
P.S. Drago mi je da ipak nije ispalo da san tolko zakržljala da ne vidin nešto totalno očito 
|
|
| [Vrh] |
|
ljpalle
Forumaš(ica)

Pridružen/a: 24. 09. 2011. (10:10:43)
Postovi: (22)16
|
 Postano: 11:54 ned, 22. 5. 2016 Naslov: Postano: 11:54 ned, 22. 5. 2016 Naslov: |
    |
|
|
[quote]Mislilo se da je [tex]\lim_n (n L) = 1[/tex] (bar san ja tako svatila rješenja). [/quote]
Prvo treba malo pripaziti jer imam malo drugacije oznake (jer OP ima ocitu gresku; [tex]L[/tex] je prema njemu samo broj, pa je trazeni limes trivijalan). Drugo, ako dobro shvacam sto zelis reci, da je (prema mojim oznakama) [tex]L(x) = 1[/tex], to je prema gornjem racunu nemoguce ako nisam napravio gresku; lako se pokaze da za dovoljno veliki [tex]x[/tex] je [tex]S(x) < x[/tex], pa i [tex]L(x) < 1[/tex].
[quote]Točan odgovor je navodno 7 (a uvrštavanjem dovoljno velikih brojeva u Wolfram alphu mogu naslutiti da bi rješenje bilo \frac{1}{6} , šta bi odgovaralo tom kao točnom odgovoru).[/quote]
Ipak sam uspio naci rjesenje. Ideja je zapravo jednostavna. Prvo supstituiramo [tex]2^{n-1}[/tex] te sumiramo u 'suprotnom smjeru' tako da singularitet bude u 0. Tada se trazi limes niza
[dtex]
L_n' = \frac{1}{4n} \frac{1}{n} \sum_{r=1}^{n} \cot^2 ( \frac{\pi}{2} \frac{r}{n} ).
[/dtex]
Ideja je sada oduzeti Riemannovu sumu koja oponasa [tex]x \mapsto 1/x^2[/tex]; motivacija je za to da se tako otprilike ponasa [tex]\cot^2 = 1 / \tan^2[/tex] u nuli s desne strane. Dakle, definiramo li funkciju [tex]g(x) = cot^2 x - 1/x^2[/tex], vidimo da se trazi limes niza
[dtex]
L_n' = \frac{1}{4 n^2} \sum_{r=1}^{n} g(\frac{\pi}{2} \frac{r}{n}) + \frac{1}{4 n^2} \sum_{r=1}^{n} \frac{4}{\pi^2} \frac{n^2}{r^2} = \frac{1}{4 n^2} \sum_{r=1}^{n} g(\frac{\pi}{2} \frac{r}{n}) + \sum_{r=1}^{n} \frac{1}{\pi^2 r^2}.
[/dtex]
Sada standardnim razmatranjima se pokaze da se [tex]g[/tex] oko nule ponasa kao [tex]x \mapsto 1/x[/tex] pa je prvi clan u nizu za veliki [tex]n[/tex] otprilike const [tex] \frac{\ln n}{n}[/tex], tj. tezi u [tex]0[/tex]. Slijedi
[dtex]
\lim_n L_n' = \pi^{-2} \sum_{r=1}^{\infty} \frac{1}{r^2} = \frac{1}{6}.
[/dtex]
| Citat: | | Mislilo se da je [tex]\lim_n (n L) = 1[/tex] (bar san ja tako svatila rješenja). |
Prvo treba malo pripaziti jer imam malo drugacije oznake (jer OP ima ocitu gresku; [tex]L[/tex] je prema njemu samo broj, pa je trazeni limes trivijalan). Drugo, ako dobro shvacam sto zelis reci, da je (prema mojim oznakama) [tex]L(x) = 1[/tex], to je prema gornjem racunu nemoguce ako nisam napravio gresku; lako se pokaze da za dovoljno veliki [tex]x[/tex] je [tex]S(x) < x[/tex], pa i [tex]L(x) < 1[/tex].
| Citat: | | Točan odgovor je navodno 7 (a uvrštavanjem dovoljno velikih brojeva u Wolfram alphu mogu naslutiti da bi rješenje bilo \frac{1}{6} , šta bi odgovaralo tom kao točnom odgovoru). |
Ipak sam uspio naci rjesenje. Ideja je zapravo jednostavna. Prvo supstituiramo [tex]2^{n-1}[/tex] te sumiramo u 'suprotnom smjeru' tako da singularitet bude u 0. Tada se trazi limes niza
[dtex]
L_n' = \frac{1}{4n} \frac{1}{n} \sum_{r=1}^{n} \cot^2 ( \frac{\pi}{2} \frac{r}{n} ).
[/dtex]
Ideja je sada oduzeti Riemannovu sumu koja oponasa [tex]x \mapsto 1/x^2[/tex]; motivacija je za to da se tako otprilike ponasa [tex]\cot^2 = 1 / \tan^2[/tex] u nuli s desne strane. Dakle, definiramo li funkciju [tex]g(x) = cot^2 x - 1/x^2[/tex], vidimo da se trazi limes niza
[dtex]
L_n' = \frac{1}{4 n^2} \sum_{r=1}^{n} g(\frac{\pi}{2} \frac{r}{n}) + \frac{1}{4 n^2} \sum_{r=1}^{n} \frac{4}{\pi^2} \frac{n^2}{r^2} = \frac{1}{4 n^2} \sum_{r=1}^{n} g(\frac{\pi}{2} \frac{r}{n}) + \sum_{r=1}^{n} \frac{1}{\pi^2 r^2}.
[/dtex]
Sada standardnim razmatranjima se pokaze da se [tex]g[/tex] oko nule ponasa kao [tex]x \mapsto 1/x[/tex] pa je prvi clan u nizu za veliki [tex]n[/tex] otprilike const [tex] \frac{\ln n}{n}[/tex], tj. tezi u [tex]0[/tex]. Slijedi
[dtex]
\lim_n L_n' = \pi^{-2} \sum_{r=1}^{\infty} \frac{1}{r^2} = \frac{1}{6}.
[/dtex]
|
|
| [Vrh] |
|
Mala_022
Forumaš(ica)
Pridružen/a: 21. 01. 2006. (18:15:12)
Postovi: (73)16
Spol: 
Lokacija: ...evo mene među moje...
|
 Postano: 18:30 ned, 22. 5. 2016 Naslov: Postano: 18:30 ned, 22. 5. 2016 Naslov: |
    |
|
|
[quote="ljpalle"]Prvo treba malo pripaziti jer imam malo drugacije oznake (jer OP ima ocitu gresku; [tex]L[/tex] je prema njemu samo broj, pa je trazeni limes trivijalan). Drugo, ako dobro shvacam sto zelis reci, da je (prema mojim oznakama) [tex]L(x) = 1[/tex], to je prema gornjem racunu nemoguce ako nisam napravio gresku; lako se pokaze da za dovoljno veliki [tex]x[/tex] je [tex]S(x) < x[/tex], pa i [tex]L(x) < 1[/tex].[/quote]
Zato san i rekla da mi ništa nije jasno.
Naime, prema tvojin oznakama ja san jedino prije postanja zadatka uspila dobiti da je [tex]L(x)\le 1[/tex] i ovisno o tome šta san ubacivala u Wolfram alphu umisto [tex]x[/tex] dobivala bi različite rezultate za [tex]L(x)[/tex]. A zadatak san prepisala točno kako piše (dakle, nema nikakvih pretpostavki i zahtjeva za [tex]x[/tex]). E, sad, šta su autori tili napisati mislin da nikad nećemo saznati. Al da me zadatak izluđuje, izluđuje me :faint:
[quote="ljpalle"]Ipak sam uspio naci rjesenje. Ideja je zapravo jednostavna. Prvo supstituiramo [tex]2^{n-1}[/tex] te sumiramo u 'suprotnom smjeru' tako da singularitet bude u 0. Tada se trazi limes niza
[dtex]
L_n' = \frac{1}{4n} \frac{1}{n} \sum_{r=1}^{n} \cot^2 ( \frac{\pi}{2} \frac{r}{n} ).
[/dtex]
Ideja je sada oduzeti Riemannovu sumu koja oponasa [tex]x \mapsto 1/x^2[/tex]; motivacija je za to da se tako otprilike ponasa [tex]\cot^2 = 1 / \tan^2[/tex] u nuli s desne strane. Dakle, definiramo li funkciju [tex]g(x) = cot^2 x - 1/x^2[/tex], vidimo da se trazi limes niza
[dtex]
L_n' = \frac{1}{4 n^2} \sum_{r=1}^{n} g(\frac{\pi}{2} \frac{r}{n}) + \frac{1}{4 n^2} \sum_{r=1}^{n} \frac{4}{\pi^2} \frac{n^2}{r^2} = \frac{1}{4 n^2} \sum_{r=1}^{n} g(\frac{\pi}{2} \frac{r}{n}) + \sum_{r=1}^{n} \frac{1}{\pi^2 r^2}.
[/dtex]
Sada standardnim razmatranjima se pokaze da se [tex]g[/tex] oko nule ponasa kao [tex]x \mapsto 1/x[/tex] pa je prvi clan u nizu za veliki [tex]n[/tex] otprilike const [tex] \frac{\ln n}{n}[/tex], tj. tezi u [tex]0[/tex]. Slijedi
[dtex]
\lim_n L_n' = \pi^{-2} \sum_{r=1}^{\infty} \frac{1}{r^2} = \frac{1}{6}.
[/dtex][/quote]
Triba se toga svega sititi :thumbup:
Svaka čast :respekt:
| ljpalle (napisa): | | Prvo treba malo pripaziti jer imam malo drugacije oznake (jer OP ima ocitu gresku; [tex]L[/tex] je prema njemu samo broj, pa je trazeni limes trivijalan). Drugo, ako dobro shvacam sto zelis reci, da je (prema mojim oznakama) [tex]L(x) = 1[/tex], to je prema gornjem racunu nemoguce ako nisam napravio gresku; lako se pokaze da za dovoljno veliki [tex]x[/tex] je [tex]S(x) < x[/tex], pa i [tex]L(x) < 1[/tex]. |
Zato san i rekla da mi ništa nije jasno.
Naime, prema tvojin oznakama ja san jedino prije postanja zadatka uspila dobiti da je [tex]L(x)\le 1[/tex] i ovisno o tome šta san ubacivala u Wolfram alphu umisto [tex]x[/tex] dobivala bi različite rezultate za [tex]L(x)[/tex]. A zadatak san prepisala točno kako piše (dakle, nema nikakvih pretpostavki i zahtjeva za [tex]x[/tex]). E, sad, šta su autori tili napisati mislin da nikad nećemo saznati. Al da me zadatak izluđuje, izluđuje me 
| ljpalle (napisa): | Ipak sam uspio naci rjesenje. Ideja je zapravo jednostavna. Prvo supstituiramo [tex]2^{n-1}[/tex] te sumiramo u 'suprotnom smjeru' tako da singularitet bude u 0. Tada se trazi limes niza
[dtex]
L_n' = \frac{1}{4n} \frac{1}{n} \sum_{r=1}^{n} \cot^2 ( \frac{\pi}{2} \frac{r}{n} ).
[/dtex]
Ideja je sada oduzeti Riemannovu sumu koja oponasa [tex]x \mapsto 1/x^2[/tex]; motivacija je za to da se tako otprilike ponasa [tex]\cot^2 = 1 / \tan^2[/tex] u nuli s desne strane. Dakle, definiramo li funkciju [tex]g(x) = cot^2 x - 1/x^2[/tex], vidimo da se trazi limes niza
[dtex]
L_n' = \frac{1}{4 n^2} \sum_{r=1}^{n} g(\frac{\pi}{2} \frac{r}{n}) + \frac{1}{4 n^2} \sum_{r=1}^{n} \frac{4}{\pi^2} \frac{n^2}{r^2} = \frac{1}{4 n^2} \sum_{r=1}^{n} g(\frac{\pi}{2} \frac{r}{n}) + \sum_{r=1}^{n} \frac{1}{\pi^2 r^2}.
[/dtex]
Sada standardnim razmatranjima se pokaze da se [tex]g[/tex] oko nule ponasa kao [tex]x \mapsto 1/x[/tex] pa je prvi clan u nizu za veliki [tex]n[/tex] otprilike const [tex] \frac{\ln n}{n}[/tex], tj. tezi u [tex]0[/tex]. Slijedi
[dtex]
\lim_n L_n' = \pi^{-2} \sum_{r=1}^{\infty} \frac{1}{r^2} = \frac{1}{6}.
[/dtex] |
Triba se toga svega sititi 
Svaka čast 
|
|
| [Vrh] |
|
|







