| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
krilo
Forumaš(ica)


Pridružen/a: 01. 11. 2016. (14:45:48)
Postovi: (4E)16
Spol: 
|
 Postano: 11:53 ned, 14. 1. 2018 Naslov: Ideali u Z[i] Postano: 11:53 ned, 14. 1. 2018 Naslov: Ideali u Z[i] |
    |
|
|
Pozdrav!
Rješavajući kolokvije nalazim puno zadataka s idealima koji uglavnom idu na isti kalup, ali ih ne znam riješiti. Konkretno, bi li mi tko znao objasniti koji je postupak za rješavanje zadataka tipa (2. kol. 2017., 4. zad)
U prstenu [tex]Z[i][/tex] promatramo ideal [tex]I = (3 + i, 12i).[/tex]
a) Je li [tex]I[/tex] glavni ideal i ako jest, prikažite ga kao takvog.
b) Je li i prost? Je li maksimalan?
Znam definicije glavnog ideala, prostosti i maksimalnosti, ali mi nije jasno kako doći do odgovora na ova pitanja. Od čega krenuti i s čime završiti? Hvala unaprijed. )
Pozdrav!
Rješavajući kolokvije nalazim puno zadataka s idealima koji uglavnom idu na isti kalup, ali ih ne znam riješiti. Konkretno, bi li mi tko znao objasniti koji je postupak za rješavanje zadataka tipa (2. kol. 2017., 4. zad)
U prstenu [tex]Z[i][/tex] promatramo ideal [tex]I = (3 + i, 12i).[/tex]
a) Je li [tex]I[/tex] glavni ideal i ako jest, prikažite ga kao takvog.
b) Je li i prost? Je li maksimalan?
Znam definicije glavnog ideala, prostosti i maksimalnosti, ali mi nije jasno kako doći do odgovora na ova pitanja. Od čega krenuti i s čime završiti? Hvala unaprijed. 
|
|
| [Vrh] |
|
goranm
Forumaš(ica)


Pridružen/a: 12. 11. 2002. (20:09:12)
Postovi: (906)16
Spol: 
|
 Postano: 9:55 sub, 20. 1. 2018 Naslov: Postano: 9:55 sub, 20. 1. 2018 Naslov: |
    |
|
|
Kako je [tex]\mathbb Z[i][/tex] domena glavnih ideala, onda ti je jasno koji je odgovor na prvi dio u a). Opet, s obzirom da je [tex]\mathbb Z[i][/tex] domena glavnih ideala, onda ideal (a,b) je ujedno generiran elementom nzd(a,b), gdje je nzd najveci zajednicki djelitelj. Znaci, trebas izracunati nzd(3+i,12i).
Sto se tice b), kako znamo da u domeni glavnih ideala (s jedinicom) ne-nul ideali su prosti ako i samo ako su maksimalni, tada odgovorom na jedno pitanje dobivamo odgovor i na drugo.
Kako bi utvrdili je li I=(nzd(3+i,12i)) najlakse je iskoristiti svojstva funkcije [tex]\varphi\colon a+bi\mapsto a^2+b^2[/tex]. Detalji se mogu pronaci i u skripti s vjezbi.
Kako je [tex]\mathbb Z[i][/tex] domena glavnih ideala, onda ti je jasno koji je odgovor na prvi dio u a). Opet, s obzirom da je [tex]\mathbb Z[i][/tex] domena glavnih ideala, onda ideal (a,b) je ujedno generiran elementom nzd(a,b), gdje je nzd najveci zajednicki djelitelj. Znaci, trebas izracunati nzd(3+i,12i).
Sto se tice b), kako znamo da u domeni glavnih ideala (s jedinicom) ne-nul ideali su prosti ako i samo ako su maksimalni, tada odgovorom na jedno pitanje dobivamo odgovor i na drugo.
Kako bi utvrdili je li I=(nzd(3+i,12i)) najlakse je iskoristiti svojstva funkcije [tex]\varphi\colon a+bi\mapsto a^2+b^2[/tex]. Detalji se mogu pronaci i u skripti s vjezbi.
_________________
The Dude Abides
|
|
| [Vrh] |
|
anabella
Forumaš(ica)

Pridružen/a: 11. 11. 2016. (18:51:13)
Postovi: (1)16
Lokacija: Zagreb
|
|
| [Vrh] |
|
Gost
|
 Postano: 17:25 pon, 22. 1. 2018 Naslov: Postano: 17:25 pon, 22. 1. 2018 Naslov: |
    |
|
|
Prvo pitanje stvarno ne razumijem, a drugo pitanje se bojim ista hintat jer se bojim da cu te samo odvest na krivi put sto god da kazem, pa evo rjesenje (za koje se nadam da je u redu):
Pretpostavimo da je [tex]f(a) = f(1)[/tex], te podijelimo [tex]1[/tex] sa [tex]a[/tex]. Preciznije, po teoremu o dijeljenju u Euklidovoj domeni, imamo
[latex]1 = aq + r,[/latex]
pri cemu su [tex] r, q \in A[/tex], te [tex]f(r) < f(a) = f(1)[/tex]. Dvije su mogucnosti; [tex]r = 0[/tex] ili [tex]r \ne 0[/tex]. Ako je nastupila prva mogucnost, onda je [tex]aq = 1[/tex], tj [tex]a[/tex] je invertibilan. Dokazimo da je druga mogucnost nemoguca.
Naime, tada bi bilo [tex]r = 1-aq[/tex], tj.
[latex]f(r) = f(1-aq) = f(1(1-aq)) \geq f(1),[/latex]
sto je kontradikcija sa od prije navedenim ([tex]f(r) < f(a) = f(1)[/tex]).
Prvo pitanje stvarno ne razumijem, a drugo pitanje se bojim ista hintat jer se bojim da cu te samo odvest na krivi put sto god da kazem, pa evo rjesenje (za koje se nadam da je u redu):
Pretpostavimo da je [tex]f(a) = f(1)[/tex], te podijelimo [tex]1[/tex] sa [tex]a[/tex]. Preciznije, po teoremu o dijeljenju u Euklidovoj domeni, imamo
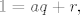
pri cemu su [tex] r, q \in A[/tex], te [tex]f(r) < f(a) = f(1)[/tex]. Dvije su mogucnosti; [tex]r = 0[/tex] ili [tex]r \ne 0[/tex]. Ako je nastupila prva mogucnost, onda je [tex]aq = 1[/tex], tj [tex]a[/tex] je invertibilan. Dokazimo da je druga mogucnost nemoguca.
Naime, tada bi bilo [tex]r = 1-aq[/tex], tj.
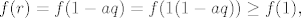
sto je kontradikcija sa od prije navedenim ([tex]f(r) < f(a) = f(1)[/tex]).
|
|
| [Vrh] |
|
krilo
Forumaš(ica)


Pridružen/a: 01. 11. 2016. (14:45:48)
Postovi: (4E)16
Spol: 
|
 Postano: 19:25 uto, 23. 1. 2018 Naslov: Postano: 19:25 uto, 23. 1. 2018 Naslov: |
    |
|
|
Imam par pitanja vezano za zadatke iz kolokvija https://web.math.pmf.unizg.hr/nastava/alg/2015-16/PopAS2016_nast.pdf
1. U 4. zadatku traži se jezgra. Nakon nešto raspisa, dolazim do zaključka da mora vrijediti [tex]p(-1)=1=p(1)[/tex], ali tu ne vidim neki operativan raspis koji bi mi pomogao konkretno odrediti jezgru. Dalo bi se podijeliti taj uvjet na slučajeve kad je stupanj polinoma paran ili neparan, pa da se onda uvrste -1 i 1, ali to me dovede do uvjeta [dtex]a_{n-1}+a_{n-3}+...+a_{1}=0[/dtex] kada je [tex]st(p)=n=2k, k \in N[/tex] i [dtex]a_{n}+a_{n-2}+...+a_{1}=0[/dtex] kada je [tex]st(p)=n=2k+1, k \in N[/tex], gdje su [tex]a_{i}[/tex] koeficijeni polinoma p. Ima tko ideju kako to srediti i odrediti je li ta jezgra prost ideal?
2. U 5. zadatku, kako se iščarobiraju ti homomorfizmi? Iz uvjeta da se jedinica preslikava u jedinicu i aditivnosti dobijem [dtex]\omega(a \in Z)=\omega(1+...+1)=\omega(1) \cdot a=a[/dtex] i dalje od toga ne znam. Kako se domoći nekih uvjeta za "korjeniti" dio elementa [tex]a+b\sqrt{2} \in Z[\sqrt{2}][/tex]?
Imam par pitanja vezano za zadatke iz kolokvija https://web.math.pmf.unizg.hr/nastava/alg/2015-16/PopAS2016_nast.pdf
1. U 4. zadatku traži se jezgra. Nakon nešto raspisa, dolazim do zaključka da mora vrijediti [tex]p(-1)=1=p(1)[/tex], ali tu ne vidim neki operativan raspis koji bi mi pomogao konkretno odrediti jezgru. Dalo bi se podijeliti taj uvjet na slučajeve kad je stupanj polinoma paran ili neparan, pa da se onda uvrste -1 i 1, ali to me dovede do uvjeta [dtex]a_{n-1}+a_{n-3}+...+a_{1}=0[/dtex] kada je [tex]st(p)=n=2k, k \in N[/tex] i [dtex]a_{n}+a_{n-2}+...+a_{1}=0[/dtex] kada je [tex]st(p)=n=2k+1, k \in N[/tex], gdje su [tex]a_{i}[/tex] koeficijeni polinoma p. Ima tko ideju kako to srediti i odrediti je li ta jezgra prost ideal?
2. U 5. zadatku, kako se iščarobiraju ti homomorfizmi? Iz uvjeta da se jedinica preslikava u jedinicu i aditivnosti dobijem [dtex]\omega(a \in Z)=\omega(1+...+1)=\omega(1) \cdot a=a[/dtex] i dalje od toga ne znam. Kako se domoći nekih uvjeta za "korjeniti" dio elementa [tex]a+b\sqrt{2} \in Z[\sqrt{2}][/tex]?
|
|
| [Vrh] |
|
goranm
Forumaš(ica)


Pridružen/a: 12. 11. 2002. (20:09:12)
Postovi: (906)16
Spol: 
|
 Postano: 20:51 sri, 24. 1. 2018 Naslov: Postano: 20:51 sri, 24. 1. 2018 Naslov: |
    |
|
|
[quote="krilo"]1. U 4. zadatku traži se jezgra. Nakon nešto raspisa, dolazim do zaključka da mora vrijediti [tex]p(-1)=1=p(1)[/tex], ali tu ne vidim neki operativan raspis koji bi mi pomogao konkretno odrediti jezgru. Dalo bi se podijeliti taj uvjet na slučajeve kad je stupanj polinoma paran ili neparan, pa da se onda uvrste -1 i 1, ali to me dovede do uvjeta[/quote]
Pripazi ovdje, jer kad pricamo o homomorfizmima [b]prstena[/b], onda jezgra gadja [b]aditivni[/b] neutralni element u [tex]M_2(\mathbb Z)[/tex], odnosno nul-matricu, a ne [tex]I_2[/tex]. Kada bi ovo gore bio slucaj, onda bi p(x)=1 bio u jezgri, pa bi jezgra sadrzavala invertibilan element, a sto bi znacilo da bi morala biti jednaka citavom prstenu (jer ako ideal I u prstenu R sadrzi 1, onda je r1 u I za svaki r iz R pa je I=R), sto ocito nije slucaj. Relacija vezana uz [tex]I_2[/tex] koju f mora zadovoljavati je [tex]f(1)=I_2[/tex], sto je ocito slucaj.
Uvjet [tex]p(-1)=0=p(1)[/tex] znaci da p ima nultocke u 1 i -1, odnosno [tex]p(x)=(x-1)(x+1)g(x)[/tex], gdje je g bilo koji polinom u Z[x]. U prijevodu, to znaci da je p u idealu generiranom s (x-1)(x+1).
[size=9][color=#999999]Added after 16 minutes:[/color][/size]
[quote="krilo"]2. U 5. zadatku, kako se iščarobiraju ti homomorfizmi? Iz uvjeta da se jedinica preslikava u jedinicu i aditivnosti dobijem [dtex]\omega(a \in Z)=\omega(1+...+1)=\omega(1) \cdot a=a[/dtex] i dalje od toga ne znam. Kako se domoći nekih uvjeta za "korjeniti" dio elementa [tex]a+b\sqrt{2} \in Z[\sqrt{2}][/tex]?[/quote]
[dtex]w(b\sqrt 2)=w((b+0\cdot\sqrt 2)(0+\sqrt 2))=w(b+0\cdot\sqrt 2)\cdot w(0+\sqrt 2)=w(b)w(\sqrt 2)=bw(\sqrt 2).[/dtex]
Isto tako,
[dtex]w(a+b\sqrt 2)=w((a+0\cdot\sqrt 2)+(0+b\sqrt 2))=w(a)+w(b\sqrt 2)=a+bw(\sqrt 2).[/dtex]
| krilo (napisa): | | 1. U 4. zadatku traži se jezgra. Nakon nešto raspisa, dolazim do zaključka da mora vrijediti [tex]p(-1)=1=p(1)[/tex], ali tu ne vidim neki operativan raspis koji bi mi pomogao konkretno odrediti jezgru. Dalo bi se podijeliti taj uvjet na slučajeve kad je stupanj polinoma paran ili neparan, pa da se onda uvrste -1 i 1, ali to me dovede do uvjeta |
Pripazi ovdje, jer kad pricamo o homomorfizmima prstena, onda jezgra gadja aditivni neutralni element u [tex]M_2(\mathbb Z)[/tex], odnosno nul-matricu, a ne [tex]I_2[/tex]. Kada bi ovo gore bio slucaj, onda bi p(x)=1 bio u jezgri, pa bi jezgra sadrzavala invertibilan element, a sto bi znacilo da bi morala biti jednaka citavom prstenu (jer ako ideal I u prstenu R sadrzi 1, onda je r1 u I za svaki r iz R pa je I=R), sto ocito nije slucaj. Relacija vezana uz [tex]I_2[/tex] koju f mora zadovoljavati je [tex]f(1)=I_2[/tex], sto je ocito slucaj.
Uvjet [tex]p(-1)=0=p(1)[/tex] znaci da p ima nultocke u 1 i -1, odnosno [tex]p(x)=(x-1)(x+1)g(x)[/tex], gdje je g bilo koji polinom u Z[x]. U prijevodu, to znaci da je p u idealu generiranom s (x-1)(x+1).
Added after 16 minutes:
| krilo (napisa): | | 2. U 5. zadatku, kako se iščarobiraju ti homomorfizmi? Iz uvjeta da se jedinica preslikava u jedinicu i aditivnosti dobijem [dtex]\omega(a \in Z)=\omega(1+...+1)=\omega(1) \cdot a=a[/dtex] i dalje od toga ne znam. Kako se domoći nekih uvjeta za "korjeniti" dio elementa [tex]a+b\sqrt{2} \in Z[\sqrt{2}][/tex]? |
[dtex]w(b\sqrt 2)=w((b+0\cdot\sqrt 2)(0+\sqrt 2))=w(b+0\cdot\sqrt 2)\cdot w(0+\sqrt 2)=w(b)w(\sqrt 2)=bw(\sqrt 2).[/dtex]
Isto tako,
[dtex]w(a+b\sqrt 2)=w((a+0\cdot\sqrt 2)+(0+b\sqrt 2))=w(a)+w(b\sqrt 2)=a+bw(\sqrt 2).[/dtex]
_________________
The Dude Abides
Zadnja promjena: goranm; 21:17 pet, 26. 1. 2018; ukupno mijenjano 2 put/a.
|
|
| [Vrh] |
|
goranm
Forumaš(ica)


Pridružen/a: 12. 11. 2002. (20:09:12)
Postovi: (906)16
Spol: 
|
|
| [Vrh] |
|
|









