| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
ZELENIZUBNAPLANETIDO
SADE
Forumaš(ica)
Pridružen/a: 04. 03. 2004. (19:56:15)
Postovi: (54F)16
Lokacija: hm?
|
 Postano: 17:37 pon, 4. 10. 2004 Naslov: Definicija vanjske sile, Hookeov zakon i jednadjba ravnoteze |
    |
|
|
:shock: opet ja :shock:
Dakle:
[quote="prof. Caklovic u skripti"]Deformacija uzrokuje unutarnja naprezanja u stapu za koja pretpostavljamo da su proporcionalna sa e(x). Sila naprezanja je dana formulom:
[latex] w(x):=c(x) \cdot \frac d{dx}u(x)[/latex]
gdje je c pozitivna fja. To je Hookeov zakon za stap, a gornja relacija izmedju naprezanja i progiba je definicija elasticnog materijala (stapa). Funkcija c ovisi o kvaliteti materijala i to je sila naprezanja u tocki x za jedinicnu mjeru deformacije. Sila naprezanja w je kontaktna sila kojom dio stapa desno od x djeluje na dio stapa lijevo od x jer dijelovi kontaktiraju preko zajednickog presjeka. Za razliku od w vanjska sila
[latex]F(x, x+\Delta x)[/latex]
na dio stapa [latex]<x,x+\Delta x>[/latex] je "volumnog" karaktera i u vecini slucajeva moze se zapisati kao integral svoje gustoce
[latex]\displaystyle F(x, x+\Delta x)= \int^{x+\Delta x}_x f(x)dx[/latex]
Posebno je interesantno koncentrirano djelovanje u tocki [i]xi[/i], koje nije gornjeg tipa, i mozemo ga zapisati kao:
[latex]\displaystyle F(x, x+\Delta x)= \left\{ \begin{array}{cl}F, & x \leq \xi \leq x+\Delta x \\ 0, & ~inace~\end{array} \right.[/latex]
Jednadjba ravnoteze dijela stapa [latex]<x, x+\Delta x>[/latex] je sada:
[latex]w(x+\Delta x)-w(x)+F(x, x+\Delta x)=0[/latex]
[/quote]
:blueshock:
Dakle:
[list](1) sto znaci da je neka sila [i]"kontaktna sila"[/i]
(2) ...i po cemu se zakljucuje da proporcionalna vrijednost derivacije progiba u tocki stvara funkcijsku ovisnost [i]"dijela stapa desno od x"[/i] sa dijelom stapa [i]"lijevo od x" "jer djelovi kontaktiraju preko zajednickog presjeka"[/i] :shocked!: sto god taj zajednicki presjek bio :cry:
(3) sto znaci da je vanjska sila [i]""volumnog""[/i] karaktera :shock:?
(4) ..i kako to misli [i]"svoje gustoce"[/i] :shock: ...i odkud funkcija f :?
(5) po cemu se [i]"posebno interesantno koncentrirano djelovanje u tocki xi"[/i] razlikuje od [i]"gornjeg tipa"[/i], kojeg [i]"ona nije"[/i] :shock: i kakvu ulogu tocno ima varijabla xi u definiciji tog [i]"drukcijeg tipa"[/i] :shocked!:
(6) kada kaze da je [i]"jednadjba ravnoteze sada"[/i], da li on to nju definira ili logicki zakljucuje iz nekih prethodnih cinjenica koje mi promicu? :shock:[/list:u]
:roll: :grrr: :pavati:
:veky:
 opet ja
Dakle:
| prof. Caklovic u skripti (napisa): | Deformacija uzrokuje unutarnja naprezanja u stapu za koja pretpostavljamo da su proporcionalna sa e(x). Sila naprezanja je dana formulom:
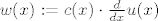
gdje je c pozitivna fja. To je Hookeov zakon za stap, a gornja relacija izmedju naprezanja i progiba je definicija elasticnog materijala (stapa). Funkcija c ovisi o kvaliteti materijala i to je sila naprezanja u tocki x za jedinicnu mjeru deformacije. Sila naprezanja w je kontaktna sila kojom dio stapa desno od x djeluje na dio stapa lijevo od x jer dijelovi kontaktiraju preko zajednickog presjeka. Za razliku od w vanjska sila
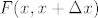
na dio stapa  je "volumnog" karaktera i u vecini slucajeva moze se zapisati kao integral svoje gustoce
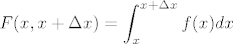
Posebno je interesantno koncentrirano djelovanje u tocki xi, koje nije gornjeg tipa, i mozemo ga zapisati kao:
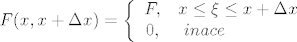
Jednadjba ravnoteze dijela stapa  je sada:
|
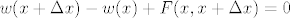
Dakle:
(1) sto znaci da je neka sila "kontaktna sila"
(2) ...i po cemu se zakljucuje da proporcionalna vrijednost derivacije progiba u tocki stvara funkcijsku ovisnost "dijela stapa desno od x" sa dijelom stapa "lijevo od x" "jer djelovi kontaktiraju preko zajednickog presjeka"  sto god taj zajednicki presjek bio 
(3) sto znaci da je vanjska sila ""volumnog"" karaktera ?
(4) ..i kako to misli "svoje gustoce" ...i odkud funkcija f 
(5) po cemu se "posebno interesantno koncentrirano djelovanje u tocki xi" razlikuje od "gornjeg tipa", kojeg "ona nije" i kakvu ulogu tocno ima varijabla xi u definiciji tog "drukcijeg tipa"
(6) kada kaze da je "jednadjba ravnoteze sada", da li on to nju definira ili logicki zakljucuje iz nekih prethodnih cinjenica koje mi promicu?
  
:veky:
_________________ 
Pupoljak nije negiran. Rekao sam to i ponovit cu to jos jedanput. Pupoljak NIJE negirAn.
MADD
(Mothers Against Dirty Dialectics)
Based on a true story. NOT.
Ko ih sljivi, mi sviramo punk  |
|
| [Vrh] |
|
ZELENIZUBNAPLANETIDO
SADE
Forumaš(ica)
Pridružen/a: 04. 03. 2004. (19:56:15)
Postovi: (54F)16
Lokacija: hm?
|
|
| [Vrh] |
|
veky
Forumaš(ica)
Pridružen/a: 09. 12. 2002. (19:59:43)
Postovi: (5B0)16
Lokacija: negdje daleko...
|
| Postano: 22:24 pon, 4. 10. 2004 Naslov: Re: Definicija vanjske sile, Hookeov zakon i jednadjba ravno |
|
|
|
[quote="ZELENIZUBNAPLANETIDOSADE"]:shock: opet ja :shock:[/quote]
Argh. Najradije bih te opet pozvao da dođeš na faks:-), ali se bojim da me ne napadnu sindikalci... :-o
Dakle, osuđeni smo na Forum. I imam još sat i pol da odgovorim na ovo. (-:
[quote]Dakle:
[quote="prof. Caklovic u skripti"]Deformacija uzrokuje unutarnja naprezanja u stapu za koja pretpostavljamo da su proporcionalna sa e(x). Sila naprezanja je dana formulom:
[latex] w(x):=c(x) \cdot \frac d{dx}u(x)[/latex]
gdje je c pozitivna fja. To je Hookeov zakon za stap, a gornja relacija izmedju naprezanja i progiba je definicija elasticnog materijala (stapa). Funkcija c ovisi o kvaliteti materijala i to je sila naprezanja u tocki x za jedinicnu mjeru deformacije. Sila naprezanja w je kontaktna sila kojom dio stapa desno od x djeluje na dio stapa lijevo od x jer dijelovi kontaktiraju preko zajednickog presjeka. Za razliku od w vanjska sila
[latex]F(x, x+\Delta x)[/latex]
na dio stapa [latex]<x,x+\Delta x>[/latex] je "volumnog" karaktera i u vecini slucajeva moze se zapisati kao integral svoje gustoce
[latex]\displaystyle F(x, x+\Delta x)= \int^{x+\Delta x}_x f(x)dx[/latex]
Posebno je interesantno koncentrirano djelovanje u tocki [i]xi[/i], koje nije gornjeg tipa, i mozemo ga zapisati kao:
[latex]\displaystyle F(x, x+\Delta x)= \left\{ \begin{array}{cl}F, & x \leq \xi \leq x+\Delta x \\ 0, & ~inace~\end{array} \right.[/latex]
Jednadjba ravnoteze dijela stapa [latex]<x, x+\Delta x>[/latex] je sada:
[latex]w(x+\Delta x)-w(x)+F(x, x+\Delta x)=0[/latex]
[/quote]
:blueshock:
Dakle:
[list](1) sto znaci da je neka sila [i]"kontaktna sila"[/i][/quote]
Da se, za potrebe mat.modeliranja, može promatrati kao sila za čije je djelovanje esencijalan kontakt između onoga što djeluje silom, i onoga na što sila djeluje. Npr. kad Sizif gura kamen uzbrdo (ne pitaj zašto mi je sad ovaj primjer pao na pamet :twisted: ), djeluje na njega kontaktnom silom. Za razliku od npr. gravitacijske ili magnetne sile, koja ne pretpostavlja kontakt i djeluje "na daljinu".
[quote](2) ...i po cemu se zakljucuje da proporcionalna vrijednost derivacije progiba u tocki stvara funkcijsku ovisnost [i]"dijela stapa desno od x"[/i] sa dijelom stapa [i]"lijevo od x"[/quote]
:?: Ja ovo nisam uspio naći u citiranom tekstu. A i bila bi poprilična besmislica, da jedan dio štapa funkcijski ovisi o drugom. :-D
Vjerojatno piše nešto drugo, poput funkcijske ovisnosti _sile_ (kojom jedan dio štapa djeluje na drugi) i progiba.
[quote] "jer djelovi kontaktiraju preko zajednickog presjeka"[/i] :shocked!: sto god taj zajednicki presjek bio :cry:[/quote]
Krug. U većini slučajeva. :-) No za potrebe mat.modeliranja, mislim da se može apstrahirati točkom (ako se štap može apstrahirati linijom).
[quote](3) sto znaci da je vanjska sila [i]""volumnog""[/i] karaktera :shock:?[/quote]
Hmda, još jedna alternativa pojmu "kontaktne" sile gore. Dakle, kontaktna može značiti da njeno djelovanje ovisi o dvodimenzionalnoj površini kontakta (ili, u našoj idealizaciji, samo strukturi štapa u točki x ), as opposed to "volumna" sila, što bi značilo da njeno djelovanje ovisi o trodimenzionalnom volumenu na koji djeluje (valjda najjednostavniji primjer: težina) - ili, u istoj idealizaciji kao gore, segmentu [x,x+dx] .
[quote](4) ..i kako to misli [i]"svoje gustoce"[/i] :shock: ...i odkud funkcija f :?[/quote]
Ehm. Jesi polagao UVIS? Hm... vjerojatno nisi. :-(
Dakle, općenito u teoriji mjere ("vjerojatnost" u UVISu, "vanjska sila" ovdje), bavimo se time da reprezentiramo razne 'mjere' - preslikavanja koja određenim podskupovima (za početak, osnovnim "ciglama" poput [a,b> - a pomoću njih i mnogim drugima, tzv. Borelovim skupovima) nekog prostora (npr. |R , ili u vjerojatnosti češće [0,1] ) pridružuju pozitivne realne brojeve - in a way, 'mjere' ih.
Općenit teorem o reprezentaciji je dosta zapetljan, no bît se svodi na to da postoje dvije osnovne vrste, na neki način dualne jedna drugoj:
- "apsolutno neprekidna" mjera, čiji je glavni oblik mj([a,b>):=F(b)-F(a) , gdje je F primitivna funkcija neke funkcije f . In a way, f je derivacija od F , odnosno mj([a,b>)=int{a~b}f(x)dx . F se onda (i općenitije) zove "funkcija distribucije", a f "funkcija gustoće". Naziv dolazi od toga što ako hoćeš izraziti masu nekog objekta, također integriraš gustoću duž njegovog "volumena" (u ovom slučaju [a,b> ).
- "singularna" mjera (ono što Čaklović u terminima sile zove "koncentrirano djelovanje"), čija funkcija distribucije F ima trivijalan skok prve vrste - tipa, do broja 3.27 je konstanta 0 , a nakon toga je konstanta 1 . Naravno, takva funkcija se ne može izraziti u gornjem obliku (integral od f duž [a,b> ), i kaže se da takva mjera (vjerojatnost, sila) nema gustoću.
(No uvijek su tu fizičari, kojima se gornja generalizacija Newton-Leibnizove formule sviđa, pa bi htjeli da i takva djelovanja imaju gustoću, pa je izmisle :shock: - i zovu "Diracova funkcija" ili nešto slično... uglavnom, to je "funkcija" koja je svuda nula, osim u 3.27 , gdje je kao fol beskonačno, ali tako precizno beskonačno da integral koji preko te točke prijeđe bude točno 1 ... mah)
[quote](5) po cemu se [i]"posebno interesantno koncentrirano djelovanje u tocki xi"[/i] razlikuje od [i]"gornjeg tipa"[/i], kojeg [i]"ona nije"[/i] :shock:[/quote]
Nadam se da je opisano gore.
[quote] i kakvu ulogu tocno ima varijabla xi u definiciji tog [i]"drukcijeg tipa"[/i] :shocked!:[/quote]
Ona glumi placeholder za moj broj 3.27 u gornjem... :-)
Dakle, mislim da ti je jasno da ako F(...) ima vrijednost 0 do točke ksi , a F (ah to Čaklovićevo multioznačavanje... dobro da nije R :-x ) od ksi nadalje, da će F([x,x+dx>)=F(x+dx)-F(x) biti upravo ono što dolje piše: 0 ako ksi nije u intervalu, a F ako jest.
[quote](6) kada kaze da je [i]"jednadjba ravnoteze sada"[/i], da li on to nju definira ili logicki zakljucuje iz nekih prethodnih cinjenica koje mi promicu? :shock:[/list:u]
:roll: :grrr: :pavati:
:veky:[/quote]
Mah... vjerojatno misli "za razliku od nekih drugih fizikalnih sistemâ koje prije promatrasmo...".
| ZELENIZUBNAPLANETIDOSADE (napisa): | | opet ja |
Argh. Najradije bih te opet pozvao da dođeš na faks:-), ali se bojim da me ne napadnu sindikalci... 
Dakle, osuđeni smo na Forum. I imam još sat i pol da odgovorim na ovo. (-:
| Citat: | Dakle:
| prof. Caklovic u skripti (napisa): | Deformacija uzrokuje unutarnja naprezanja u stapu za koja pretpostavljamo da su proporcionalna sa e(x). Sila naprezanja je dana formulom:
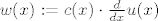
gdje je c pozitivna fja. To je Hookeov zakon za stap, a gornja relacija izmedju naprezanja i progiba je definicija elasticnog materijala (stapa). Funkcija c ovisi o kvaliteti materijala i to je sila naprezanja u tocki x za jedinicnu mjeru deformacije. Sila naprezanja w je kontaktna sila kojom dio stapa desno od x djeluje na dio stapa lijevo od x jer dijelovi kontaktiraju preko zajednickog presjeka. Za razliku od w vanjska sila
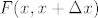
na dio stapa je "volumnog" karaktera i u vecini slucajeva moze se zapisati kao integral svoje gustoce
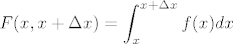
Posebno je interesantno koncentrirano djelovanje u tocki xi, koje nije gornjeg tipa, i mozemo ga zapisati kao:
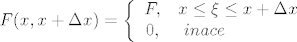
Jednadjba ravnoteze dijela stapa je sada:
|
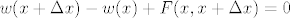
Dakle:
(1) sto znaci da je neka sila "kontaktna sila" |
Da se, za potrebe mat.modeliranja, može promatrati kao sila za čije je djelovanje esencijalan kontakt između onoga što djeluje silom, i onoga na što sila djeluje. Npr. kad Sizif gura kamen uzbrdo (ne pitaj zašto mi je sad ovaj primjer pao na pamet  ), djeluje na njega kontaktnom silom. Za razliku od npr. gravitacijske ili magnetne sile, koja ne pretpostavlja kontakt i djeluje "na daljinu".
| Citat: | | (2) ...i po cemu se zakljucuje da proporcionalna vrijednost derivacije progiba u tocki stvara funkcijsku ovisnost "dijela stapa desno od x" sa dijelom stapa "lijevo od x" |
 Ja ovo nisam uspio naći u citiranom tekstu. A i bila bi poprilična besmislica, da jedan dio štapa funkcijski ovisi o drugom. 
Vjerojatno piše nešto drugo, poput funkcijske ovisnosti _sile_ (kojom jedan dio štapa djeluje na drugi) i progiba.
| Citat: | | "jer djelovi kontaktiraju preko zajednickog presjeka" sto god taj zajednicki presjek bio |
Krug. U većini slučajeva.  No za potrebe mat.modeliranja, mislim da se može apstrahirati točkom (ako se štap može apstrahirati linijom).
| Citat: | | (3) sto znaci da je vanjska sila ""volumnog"" karaktera ? |
Hmda, još jedna alternativa pojmu "kontaktne" sile gore. Dakle, kontaktna može značiti da njeno djelovanje ovisi o dvodimenzionalnoj površini kontakta (ili, u našoj idealizaciji, samo strukturi štapa u točki x ), as opposed to "volumna" sila, što bi značilo da njeno djelovanje ovisi o trodimenzionalnom volumenu na koji djeluje (valjda najjednostavniji primjer: težina) - ili, u istoj idealizaciji kao gore, segmentu [x,x+dx] .
| Citat: | | (4) ..i kako to misli "svoje gustoce" ...i odkud funkcija f |
Ehm. Jesi polagao UVIS? Hm... vjerojatno nisi. 
Dakle, općenito u teoriji mjere ("vjerojatnost" u UVISu, "vanjska sila" ovdje), bavimo se time da reprezentiramo razne 'mjere' - preslikavanja koja određenim podskupovima (za početak, osnovnim "ciglama" poput [a,b> - a pomoću njih i mnogim drugima, tzv. Borelovim skupovima) nekog prostora (npr. |R , ili u vjerojatnosti češće [0,1] ) pridružuju pozitivne realne brojeve - in a way, 'mjere' ih.
Općenit teorem o reprezentaciji je dosta zapetljan, no bît se svodi na to da postoje dvije osnovne vrste, na neki način dualne jedna drugoj:
- "apsolutno neprekidna" mjera, čiji je glavni oblik mj([a,b>):=F(b)-F(a) , gdje je F primitivna funkcija neke funkcije f . In a way, f je derivacija od F , odnosno mj([a,b>)=int{a~b}f(x)dx . F se onda (i općenitije) zove "funkcija distribucije", a f "funkcija gustoće". Naziv dolazi od toga što ako hoćeš izraziti masu nekog objekta, također integriraš gustoću duž njegovog "volumena" (u ovom slučaju [a,b> ).
- "singularna" mjera (ono što Čaklović u terminima sile zove "koncentrirano djelovanje"), čija funkcija distribucije F ima trivijalan skok prve vrste - tipa, do broja 3.27 je konstanta 0 , a nakon toga je konstanta 1 . Naravno, takva funkcija se ne može izraziti u gornjem obliku (integral od f duž [a,b> ), i kaže se da takva mjera (vjerojatnost, sila) nema gustoću.
(No uvijek su tu fizičari, kojima se gornja generalizacija Newton-Leibnizove formule sviđa, pa bi htjeli da i takva djelovanja imaju gustoću, pa je izmisle - i zovu "Diracova funkcija" ili nešto slično... uglavnom, to je "funkcija" koja je svuda nula, osim u 3.27 , gdje je kao fol beskonačno, ali tako precizno beskonačno da integral koji preko te točke prijeđe bude točno 1 ... mah)
| Citat: | | (5) po cemu se "posebno interesantno koncentrirano djelovanje u tocki xi" razlikuje od "gornjeg tipa", kojeg "ona nije" |
Nadam se da je opisano gore.
| Citat: | | i kakvu ulogu tocno ima varijabla xi u definiciji tog "drukcijeg tipa" |
Ona glumi placeholder za moj broj 3.27 u gornjem...
Dakle, mislim da ti je jasno da ako F(...) ima vrijednost 0 do točke ksi , a F (ah to Čaklovićevo multioznačavanje... dobro da nije R  ) od ksi nadalje, da će F([x,x+dx>)=F(x+dx)-F(x) biti upravo ono što dolje piše: 0 ako ksi nije u intervalu, a F ako jest.
| Citat: | (6) kada kaze da je "jednadjba ravnoteze sada", da li on to nju definira ili logicki zakljucuje iz nekih prethodnih cinjenica koje mi promicu?
:veky: |
Mah... vjerojatno misli "za razliku od nekih drugih fizikalnih sistemâ koje prije promatrasmo...".
|
|
| [Vrh] |
|
veky
Forumaš(ica)
Pridružen/a: 09. 12. 2002. (19:59:43)
Postovi: (5B0)16
Lokacija: negdje daleko...
|
|
| [Vrh] |
|
ZELENIZUBNAPLANETIDO
SADE
Forumaš(ica)
Pridružen/a: 04. 03. 2004. (19:56:15)
Postovi: (54F)16
Lokacija: hm?
|
| Postano: 23:03 pon, 4. 10. 2004 Naslov: Re: Definicija vanjske sile, Hookeov zakon i jednadjba ravno |
|
|
|
[quote="veky"]Da se, za potrebe mat.modeliranja, može promatrati kao sila za čije je djelovanje esencijalan kontakt između onoga što djeluje silom, i onoga na što sila djeluje. Npr. kad Sizif gura kamen uzbrdo (ne pitaj zašto mi je sad ovaj primjer pao na pamet :twisted: ), djeluje na njega kontaktnom silom. Za razliku od npr. gravitacijske ili magnetne sile, koja ne pretpostavlja kontakt i djeluje "na daljinu".[/quote]
:? a Caklovic dao primjer sa gravitacijom :roll: dobro, radi se o vertikalno polozenom stapu i mjerimo "deformaciju" na pojedinim "djelovima" stapa :)
[quote="veky"][quote](2) ...i po cemu se zakljucuje da proporcionalna vrijednost derivacije progiba u tocki stvara funkcijsku ovisnost [i]"dijela stapa desno od x"[/i] sa dijelom stapa [i]"lijevo od x"[/quote]
:?: Ja ovo nisam uspio naći u citiranom tekstu. A i bila bi poprilična besmislica, da jedan dio štapa funkcijski ovisi o drugom. :-D[/quote]
[quote="skripta"]Sila naprezanja w je kontaktna sila kojom dio stapa desno od x djeluje na dio stapa lijevo od x jer dijelovi kontaktiraju preko zajednickog presjeka.[/quote]
..al mislim da sam shvatio sto je covjek mislio, I hope :)
[quote="veky"]Vjerojatno piše nešto drugo, poput funkcijske ovisnosti _sile_ (kojom jedan dio štapa djeluje na drugi) i progiba.[/quote]
Moze :)
[quote="veky"]Hmda, još jedna alternativa pojmu "kontaktne" sile gore. Dakle, kontaktna može značiti da njeno djelovanje ovisi o dvodimenzionalnoj površini kontakta (ili, u našoj idealizaciji, samo strukturi štapa u točki x ), as opposed to "volumna" sila, što bi značilo da njeno djelovanje ovisi o trodimenzionalnom volumenu na koji djeluje (valjda najjednostavniji primjer: težina) - ili, u istoj idealizaciji kao gore, segmentu [x,x+dx] .[/quote]
Oooke :) sjelo :)
[quote="veky"]Khm. Jesi polagao UVIS? Hm... vjerojatno nisi. :-(
Dakle, općenito u teoriji mjere ("vjerojatnost" u UVISu, "vanjska sila" ovdje),[/quote]
Zapravo jesam :) al na jednom krivom faksu :lol: recimo da sam povezao :)
[quote="veky"]bavimo se time da reprezentiramo razne 'mjere' - preslikavanja koja određenim podskupovima (za početak, osnovnim "ciglama" poput [a,b> - a pomoću njih i mnogim drugima, tzv. Borelovim skupovima) nekog prostora (npr. |R , ili u vjerojatnosti češće [0,1] ) pridružuju pozitivne realne brojeve - in a way, 'mjere' ih.[/quote]
Kewl :)
[quote="veky"]"singularna" mjera (ono što Čaklović u terminima sile zove "koncentrirano djelovanje"), čija funkcija distribucije F ima trivijalan skok prve vrste - tipa, do broja 3.27 je konstanta 0 , a nakon toga je konstanta 1 . Naravno, takva funkcija se ne može izraziti u gornjem obliku (integral od f duž [a,b> ), i kaže se da takva mjera (vjerojatnost, sila) nema gustoću.
(No uvijek su tu fizičari, kojima se gornja generalizacija Newton-Leibnizove formule sviđa, pa bi htjeli da i takva djelovanja imaju gustoću, pa je izmisle :shock: - i zovu "Diracova funkcija" ili nešto slično... uglavnom, to je "funkcija" koja je svuda nula, osim u 3.27 , gdje je kao fol beskonačno, ali tako precizno beskonačno da integral koji preko te točke prijeđe bude točno 1 ... mah)[/quote]
Na koji je to nacin vezano uz pricu o slaboj derivabilnosti ? :?
Ona ako sam shvatio ne voli skokove 1. vrste?
[quote="veky"][quote] i kakvu ulogu tocno ima varijabla xi u definiciji tog [i]"drukcijeg tipa"[/i] :shocked!:[/quote]
Ona glumi placeholder za moj broj 3.27 u gornjem... :-)[/quote]
Fascinantno :D
A-ha.. Jer nacin na koji je to raspisano u gornjoj definiciji jest, kao da imamo neku fju koja je konstantna na nekom segmentu i 0 drugdje i nas "posebno zanima" (al na nacin koji apsolutno ne shvacam) bas neka fiksna tocka xi iz tog segmenta :shock:
..al i tako definirani F na nikakav nacin ne ovisi o xi, osim sto definira njegovu lokaciju :shock: i nekako sam dojma da kod njegove definicije tocka x ili tocka dx glumi 3.27? :?
A-ha efekt: ili je xi ona tocka "kontrolirane beskonacnosti" za dani F, tako da njena "derivacija" bude dobro definirana i na kraju balade integrirana daje F (da, uistinu, zasto ga nije nazvao R :shock: :lol:)?
..svatio, hope so :)
[quote="veky"]Dakle, mislim da ti je jasno da ako F(...) ima vrijednost 0 do točke ksi , a F (ah to Čaklovićevo multioznačavanje... dobro da nije R :-x ) od ksi nadalje, da će F([x,x+dx>)=F(x+dx)-F(x) biti upravo ono što dolje piše: 0 ako ksi nije u intervalu, a F ako jest.[/quote]
Call me tipsy, ali.. meni ona definicija izgleda kao da se od same fje F na nikakav nacin ne ocekuje da bude direktno utjecana vrijednoscu xi :?
[quote="veky"]Mah... vjerojatno misli "za razliku od nekih drugih fizikalnih sistemâ koje prije promatrasmo...".[/quote]
:shock: nadam se :shock:
za svoje duhovno zdravlje sam pretpostavio da se radi o definiciji :g:
DODATAK:
shvatio onu pricu sa xi :) F( , ) glumi prim fju one hokus-pokus fje koju si spominjao gore koja je taman dovoljno beskonacna za nase potrebe :g: bizarno :shock: al sjelo valjda :)
takav F ne bi bio slabo derivabilan, a? :)
| veky (napisa): | | Da se, za potrebe mat.modeliranja, može promatrati kao sila za čije je djelovanje esencijalan kontakt između onoga što djeluje silom, i onoga na što sila djeluje. Npr. kad Sizif gura kamen uzbrdo (ne pitaj zašto mi je sad ovaj primjer pao na pamet ), djeluje na njega kontaktnom silom. Za razliku od npr. gravitacijske ili magnetne sile, koja ne pretpostavlja kontakt i djeluje "na daljinu". |
a Caklovic dao primjer sa gravitacijom dobro, radi se o vertikalno polozenom stapu i mjerimo "deformaciju" na pojedinim "djelovima" stapa
| veky (napisa): | | Citat: | | (2) ...i po cemu se zakljucuje da proporcionalna vrijednost derivacije progiba u tocki stvara funkcijsku ovisnost "dijela stapa desno od x" sa dijelom stapa "lijevo od x" |
Ja ovo nisam uspio naći u citiranom tekstu. A i bila bi poprilična besmislica, da jedan dio štapa funkcijski ovisi o drugom. |
| skripta (napisa): | | Sila naprezanja w je kontaktna sila kojom dio stapa desno od x djeluje na dio stapa lijevo od x jer dijelovi kontaktiraju preko zajednickog presjeka. |
..al mislim da sam shvatio sto je covjek mislio, I hope
| veky (napisa): | | Vjerojatno piše nešto drugo, poput funkcijske ovisnosti _sile_ (kojom jedan dio štapa djeluje na drugi) i progiba. |
Moze
| veky (napisa): | | Hmda, još jedna alternativa pojmu "kontaktne" sile gore. Dakle, kontaktna može značiti da njeno djelovanje ovisi o dvodimenzionalnoj površini kontakta (ili, u našoj idealizaciji, samo strukturi štapa u točki x ), as opposed to "volumna" sila, što bi značilo da njeno djelovanje ovisi o trodimenzionalnom volumenu na koji djeluje (valjda najjednostavniji primjer: težina) - ili, u istoj idealizaciji kao gore, segmentu [x,x+dx] . |
Oooke sjelo
| veky (napisa): | Khm. Jesi polagao UVIS? Hm... vjerojatno nisi.
Dakle, općenito u teoriji mjere ("vjerojatnost" u UVISu, "vanjska sila" ovdje), |
Zapravo jesam al na jednom krivom faksu  recimo da sam povezao
| veky (napisa): | | bavimo se time da reprezentiramo razne 'mjere' - preslikavanja koja određenim podskupovima (za početak, osnovnim "ciglama" poput [a,b> - a pomoću njih i mnogim drugima, tzv. Borelovim skupovima) nekog prostora (npr. |R , ili u vjerojatnosti češće [0,1] ) pridružuju pozitivne realne brojeve - in a way, 'mjere' ih. |
Kewl
| veky (napisa): | "singularna" mjera (ono što Čaklović u terminima sile zove "koncentrirano djelovanje"), čija funkcija distribucije F ima trivijalan skok prve vrste - tipa, do broja 3.27 je konstanta 0 , a nakon toga je konstanta 1 . Naravno, takva funkcija se ne može izraziti u gornjem obliku (integral od f duž [a,b> ), i kaže se da takva mjera (vjerojatnost, sila) nema gustoću.
(No uvijek su tu fizičari, kojima se gornja generalizacija Newton-Leibnizove formule sviđa, pa bi htjeli da i takva djelovanja imaju gustoću, pa je izmisle - i zovu "Diracova funkcija" ili nešto slično... uglavnom, to je "funkcija" koja je svuda nula, osim u 3.27 , gdje je kao fol beskonačno, ali tako precizno beskonačno da integral koji preko te točke prijeđe bude točno 1 ... mah) |
Na koji je to nacin vezano uz pricu o slaboj derivabilnosti ?
Ona ako sam shvatio ne voli skokove 1. vrste?
| veky (napisa): | | Citat: | | i kakvu ulogu tocno ima varijabla xi u definiciji tog [i]"drukcijeg tipa" |
Ona glumi placeholder za moj broj 3.27 u gornjem... |
Fascinantno
A-ha.. Jer nacin na koji je to raspisano u gornjoj definiciji jest, kao da imamo neku fju koja je konstantna na nekom segmentu i 0 drugdje i nas "posebno zanima" (al na nacin koji apsolutno ne shvacam) bas neka fiksna tocka xi iz tog segmenta
..al i tako definirani F na nikakav nacin ne ovisi o xi, osim sto definira njegovu lokaciju i nekako sam dojma da kod njegove definicije tocka x ili tocka dx glumi 3.27?
A-ha efekt: ili je xi ona tocka "kontrolirane beskonacnosti" za dani F, tako da njena "derivacija" bude dobro definirana i na kraju balade integrirana daje F (da, uistinu, zasto ga nije nazvao R )?
..svatio, hope so
| veky (napisa): | | Dakle, mislim da ti je jasno da ako F(...) ima vrijednost 0 do točke ksi , a F (ah to Čaklovićevo multioznačavanje... dobro da nije R ) od ksi nadalje, da će F([x,x+dx>)=F(x+dx)-F(x) biti upravo ono što dolje piše: 0 ako ksi nije u intervalu, a F ako jest. |
Call me tipsy, ali.. meni ona definicija izgleda kao da se od same fje F na nikakav nacin ne ocekuje da bude direktno utjecana vrijednoscu xi
| veky (napisa): | | Mah... vjerojatno misli "za razliku od nekih drugih fizikalnih sistemâ koje prije promatrasmo...". |
nadam se
za svoje duhovno zdravlje sam pretpostavio da se radi o definiciji 
DODATAK:
shvatio onu pricu sa xi F( , ) glumi prim fju one hokus-pokus fje koju si spominjao gore koja je taman dovoljno beskonacna za nase potrebe bizarno al sjelo valjda
takav F ne bi bio slabo derivabilan, a?
_________________
Pupoljak nije negiran. Rekao sam to i ponovit cu to jos jedanput. Pupoljak NIJE negirAn.
MADD
(Mothers Against Dirty Dialectics)
Based on a true story. NOT.
Ko ih sljivi, mi sviramo punk |
|
| [Vrh] |
|
veky
Forumaš(ica)
Pridružen/a: 09. 12. 2002. (19:59:43)
Postovi: (5B0)16
Lokacija: negdje daleko...
|
| Postano: 23:31 pon, 4. 10. 2004 Naslov: Re: Definicija vanjske sile, Hookeov zakon i jednadjba ravno |
|
|
|
Kad se sve spoji (preciznije, unira: ), ispada da si sve shvatio. :-)
Osim, možda:
[quote="ZELENIZUBNAPLANETIDOSADE"]takav F ne bi bio slabo derivabilan, a? :)[/quote]
Bi, inFact. No dobro, ovisi koliko "slabu" derivaciju si spreman priznati.
Uobičajen notion toga (bar bio kad sam ja polagao mat.modeliranje) je nešto što je "gotovo svuda" derivacija, odnosno npr. jednako derivaciji svuda osim u konačno mnogo točaka (striktnije govoreći, gledaju se klase funkcijâ, s obzirom na releq "jednake gotovo svuda"). A nulfunkcija je po toj definiciji definitivno slaba derivacija gornje funkcije.
No ako misliš na "slabu derivaciju" u smislu "gustoću", ne, ta funkcija nema gustoću. Točno.
Kad se sve spoji (preciznije, unira: ), ispada da si sve shvatio.
Osim, možda:
| ZELENIZUBNAPLANETIDOSADE (napisa): | | takav F ne bi bio slabo derivabilan, a? |
Bi, inFact. No dobro, ovisi koliko "slabu" derivaciju si spreman priznati.
Uobičajen notion toga (bar bio kad sam ja polagao mat.modeliranje) je nešto što je "gotovo svuda" derivacija, odnosno npr. jednako derivaciji svuda osim u konačno mnogo točaka (striktnije govoreći, gledaju se klase funkcijâ, s obzirom na releq "jednake gotovo svuda"). A nulfunkcija je po toj definiciji definitivno slaba derivacija gornje funkcije.
No ako misliš na "slabu derivaciju" u smislu "gustoću", ne, ta funkcija nema gustoću. Točno.
|
|
| [Vrh] |
|
ZELENIZUBNAPLANETIDO
SADE
Forumaš(ica)
Pridružen/a: 04. 03. 2004. (19:56:15)
Postovi: (54F)16
Lokacija: hm?
|
| Postano: 10:19 uto, 5. 10. 2004 Naslov: Re: Definicija vanjske sile, Hookeov zakon i jednadjba ravno |
|
|
|
[quote="veky"]Bi, inFact. No dobro, ovisi koliko "slabu" derivaciju si spreman priznati.
Uobičajen notion toga (bar bio kad sam ja polagao mat.modeliranje) je nešto što je "gotovo svuda" derivacija, odnosno npr. jednako derivaciji svuda osim u konačno mnogo točaka (striktnije govoreći, gledaju se klase funkcijâ, s obzirom na releq "jednake gotovo svuda"). A nulfunkcija je po toj definiciji definitivno slaba derivacija gornje funkcije.
No ako misliš na "slabu derivaciju" u smislu "gustoću", ne, ta funkcija nema gustoću. Točno.[/quote]
Mislio sam na..
[quote="The Skript"][latex]DEF9.5.$ Neka je $u \in L^2(I)$ i $g \in L^2(I)$ takva da vrijedi$\\
\displaystyle \forall \varphi \in C^\infty_0(I)~ ~\int_I u(x)\varphi`(x)dx=-\int_I g(x)\varphi(x)dx\\
$Tada kazemo da je $u$ \emph{slabo derivabilna} i da je $g$ njena \emph{slaba derivacija}$.[/latex][/quote]
Koliko ja shvatio... (iako jos nisam dosao do kraja poglavlja :)) uvjeti su kao i za npr. goursat-pringsheimov teorem i C-teoreme za kvadrat i krug, tj. "neprekidna i derivabilna osim mozda u konacno mnogo tocaka" (iako prof. Caklovic ima neku drugu formulaciju :)) ? :?
A-ha :) i bas imao drugo pitanje al :D Dakle "jednake gotovo svuda" znaci "jednake, osim mozda u konacno mnogo tocaka"? :)
| veky (napisa): | Bi, inFact. No dobro, ovisi koliko "slabu" derivaciju si spreman priznati.
Uobičajen notion toga (bar bio kad sam ja polagao mat.modeliranje) je nešto što je "gotovo svuda" derivacija, odnosno npr. jednako derivaciji svuda osim u konačno mnogo točaka (striktnije govoreći, gledaju se klase funkcijâ, s obzirom na releq "jednake gotovo svuda"). A nulfunkcija je po toj definiciji definitivno slaba derivacija gornje funkcije.
No ako misliš na "slabu derivaciju" u smislu "gustoću", ne, ta funkcija nema gustoću. Točno. |
Mislio sam na..
| The Skript (napisa): |  |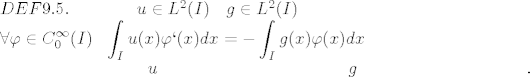
Koliko ja shvatio... (iako jos nisam dosao do kraja poglavlja ) uvjeti su kao i za npr. goursat-pringsheimov teorem i C-teoreme za kvadrat i krug, tj. "neprekidna i derivabilna osim mozda u konacno mnogo tocaka" (iako prof. Caklovic ima neku drugu formulaciju ) ?
A-ha i bas imao drugo pitanje al Dakle "jednake gotovo svuda" znaci "jednake, osim mozda u konacno mnogo tocaka"?
_________________
Pupoljak nije negiran. Rekao sam to i ponovit cu to jos jedanput. Pupoljak NIJE negirAn.
MADD
(Mothers Against Dirty Dialectics)
Based on a true story. NOT.
Ko ih sljivi, mi sviramo punk |
|
| [Vrh] |
|
veky
Forumaš(ica)
Pridružen/a: 09. 12. 2002. (19:59:43)
Postovi: (5B0)16
Lokacija: negdje daleko...
|
| Postano: 11:24 sri, 6. 10. 2004 Naslov: Re: Definicija vanjske sile, Hookeov zakon i jednadjba ravno |
|
|
|
[quote="ZELENIZUBNAPLANETIDOSADE"][quote="veky"]Bi, inFact. No dobro, ovisi koliko "slabu" derivaciju si spreman priznati.
Uobičajen notion toga (bar bio kad sam ja polagao mat.modeliranje) je nešto što je "gotovo svuda" derivacija, odnosno npr. jednako derivaciji svuda osim u konačno mnogo točaka (striktnije govoreći, gledaju se klase funkcijâ, s obzirom na releq "jednake gotovo svuda"). A nulfunkcija je po toj definiciji definitivno slaba derivacija gornje funkcije.
No ako misliš na "slabu derivaciju" u smislu "gustoću", ne, ta funkcija nema gustoću. Točno.[/quote]
Mislio sam na..
[quote="The Skript"][latex]DEF9.5.$ Neka je $u \in L^2(I)$ i $g \in L^2(I)$ takva da vrijedi$\\
\displaystyle \forall \varphi \in C^\infty_0(I)~ ~\int_I u(x)\varphi`(x)dx=-\int_I g(x)\varphi(x)dx\\
$Tada kazemo da je $u$ \emph{slabo derivabilna} i da je $g$ njena \emph{slaba derivacija}$.[/latex][/quote]
Koliko ja shvatio... (iako jos nisam dosao do kraja poglavlja :)) uvjeti su kao i za npr. goursat-pringsheimov teorem i C-teoreme za kvadrat i krug, tj. "neprekidna i derivabilna osim mozda u konacno mnogo tocaka" (iako prof. Caklovic ima neku drugu formulaciju :)) ? :?[/quote]
Uglavnom. No vidi dolje.
[quote]A-ha :) i bas imao drugo pitanje al :D Dakle "jednake gotovo svuda" znaci "jednake, osim mozda u konacno mnogo tocaka"? :)[/quote]
Ne baš, iako je to (za tebe najvažniji) poseban slučaj.
Naime, znači "jednake, osim na skupu mjere nula". Što je skup mjere nula, nadam se da znaš iz MA3. :-)
Dakle, može biti i prebrojivo. Ponekad može i neprebrojivo (znaš primjer?), no to su već perverzije... :-)
| ZELENIZUBNAPLANETIDOSADE (napisa): | | veky (napisa): | Bi, inFact. No dobro, ovisi koliko "slabu" derivaciju si spreman priznati.
Uobičajen notion toga (bar bio kad sam ja polagao mat.modeliranje) je nešto što je "gotovo svuda" derivacija, odnosno npr. jednako derivaciji svuda osim u konačno mnogo točaka (striktnije govoreći, gledaju se klase funkcijâ, s obzirom na releq "jednake gotovo svuda"). A nulfunkcija je po toj definiciji definitivno slaba derivacija gornje funkcije.
No ako misliš na "slabu derivaciju" u smislu "gustoću", ne, ta funkcija nema gustoću. Točno. |
Mislio sam na..
| The Skript (napisa): | |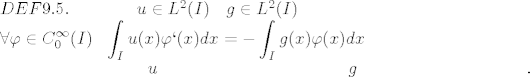
Koliko ja shvatio... (iako jos nisam dosao do kraja poglavlja ) uvjeti su kao i za npr. goursat-pringsheimov teorem i C-teoreme za kvadrat i krug, tj. "neprekidna i derivabilna osim mozda u konacno mnogo tocaka" (iako prof. Caklovic ima neku drugu formulaciju ) ? |
Uglavnom. No vidi dolje.
| Citat: | | A-ha i bas imao drugo pitanje al Dakle "jednake gotovo svuda" znaci "jednake, osim mozda u konacno mnogo tocaka"? |
Ne baš, iako je to (za tebe najvažniji) poseban slučaj.
Naime, znači "jednake, osim na skupu mjere nula". Što je skup mjere nula, nadam se da znaš iz MA3.
Dakle, može biti i prebrojivo. Ponekad može i neprebrojivo (znaš primjer?), no to su već perverzije...
|
|
| [Vrh] |
|
nenad
Moderator
Pridružen/a: 08. 10. 2002. (14:08:30)
Postovi: (355)16
|
| Postano: 19:48 pet, 22. 10. 2004 Naslov: |
|
|
|
Malo sam zakasnio, ali ipak da samo ukratko pojasnim.
Mjera i gustoća mjere:
ovdje se ne radi o reprezentaciji, nego o Radon-Nikodymovoj derivaciji. Pojednostavljeno, ako je zadana gustoća tijela, onda
masu dobivamo integrirajući gustoću po volumenu.
Singularna mjera (u odnosnu na neku drugu, kod nas volumen) je ona za koju ne postoji gustoća koja je integrabilna funkcija.
Na primjer, ako udarimo ciglu batom, sila je makroskopski djelovala trenutno, a ipak smo prenijeli konačnu količinu gibanja.
Slaba derivacija:
U ovom se kontekstu misli na derivaciju u smislu distribucija, a mjere se shvaćaju kao funkcionali na prostorima funkcija (tu se javlja teorem reprezentacije).
Vrlo grubo, derivacija funkcije Y, karakteristične funkcije R^+, može se gledati preko djelovanja na glatku funkciju f koja je nula van nekog konačnog intervala:
\int Y'f = - \int Yf' (parcijalna integracija).
Y' je čuvena Diracova masa, iznosa 1, a koncentrirana u točki 0.
Za detaljniju MATEMATIČKU razradu gornjih tema može se dijelom konzultirati i skripta (reklama :-)
N. Antonić, M. Vrdoljak: Mjera i integral,
koja bi se kod gđe. Kosjenke morala moći kupiti za 30 kn.
Nažalost, bojim se da skripta nisu lagano štivo.
- Nenad.
Malo sam zakasnio, ali ipak da samo ukratko pojasnim.
Mjera i gustoća mjere:
ovdje se ne radi o reprezentaciji, nego o Radon-Nikodymovoj derivaciji. Pojednostavljeno, ako je zadana gustoća tijela, onda
masu dobivamo integrirajući gustoću po volumenu.
Singularna mjera (u odnosnu na neku drugu, kod nas volumen) je ona za koju ne postoji gustoća koja je integrabilna funkcija.
Na primjer, ako udarimo ciglu batom, sila je makroskopski djelovala trenutno, a ipak smo prenijeli konačnu količinu gibanja.
Slaba derivacija:
U ovom se kontekstu misli na derivaciju u smislu distribucija, a mjere se shvaćaju kao funkcionali na prostorima funkcija (tu se javlja teorem reprezentacije).
Vrlo grubo, derivacija funkcije Y, karakteristične funkcije R^+, može se gledati preko djelovanja na glatku funkciju f koja je nula van nekog konačnog intervala:
\int Y'f = - \int Yf' (parcijalna integracija).
Y' je čuvena Diracova masa, iznosa 1, a koncentrirana u točki 0.
Za detaljniju MATEMATIČKU razradu gornjih tema može se dijelom konzultirati i skripta (reklama
N. Antonić, M. Vrdoljak: Mjera i integral,
koja bi se kod gđe. Kosjenke morala moći kupiti za 30 kn.
Nažalost, bojim se da skripta nisu lagano štivo.
- Nenad.
|
|
| [Vrh] |
|
|
