Search
 
 
  Engleski
 
 
 
Open in this window (click to change)
Forum@DeGiorgi: Početna
Forum za podršku nastavi na PMF-MO
Login Registracija FAQ Smajlići Članstvo Pretražnik Forum@DeGiorgi: Početna

Dal mi tko može pomoći!?

Moja sarma
 
Započnite novu temu   Odgovorite na temu   printer-friendly view    Forum@DeGiorgi: Početna -> Ostalo - ozbiljno -> Čistilište
Prethodna tema :: Sljedeća tema  
Autor/ica Poruka
2HigH
Gost
PostPostano: 16:26 sri, 19. 10. 2005    Naslov: Dal mi tko može pomoći!? Citirajte i odgovorite
Molim Vas da mi pomognete riješiti ovaj zadatak. Naime, treba izjednačiti lijevu i desnu stranu, a meni nikako to ne polazi za rukom :cry: :cry: :cry: . Unaprijed hvala! 8)

[URL=http://imageshack.us][img]http://img32.imageshack.us/img32/3332/zadatak9uq.png[/img][/URL]
Molim Vas da mi pomognete riješiti ovaj zadatak. Naime, treba izjednačiti lijevu i desnu stranu, a meni nikako to ne polazi za rukom Crying or Very sad Crying or Very sad Crying or Very sad . Unaprijed hvala! Cool



[Vrh]
vsego
Site Admin
Site Admin


Pridružen/a: 06. 10. 2002. (22:07:09)
Postovi: (3560)16
Spol: zombi
Sarma = la pohva - posuda
854 = 1068 - 214
Lokacija: /sbin/init
PostPostano: 20:47 sri, 19. 10. 2005    Naslov: Citirajte i odgovorite
[latex]$\begin{equation*}\begin{array}{l}
2^{n+2} + 2n + 1 = 2^{n+3} - n - 4 = 2 \cdot 2^{n+2} - n - 4 \\
2 \cdot 2^{n+2} - 2^{n+2} = n + 4 + 2n + 1 = 0 \\
2^{n+2} = 3n + 5
\end{array}\end{equation*}$[/latex]

Jedno rjesenje je n = 1. :) Drugih rješenja nema, jer je s lijeve strane eksponencijalna funkcija koja raste brze od linearne (s desne strane). 8) Lako dokazes deriviranjem... :)

P.S. Ako ne mora biti n € |N, onda je rjesenje i n = -1... :)


Jedno rjesenje je n = 1. Smile Drugih rješenja nema, jer je s lijeve strane eksponencijalna funkcija koja raste brze od linearne (s desne strane). Cool Lako dokazes deriviranjem... Smile

P.S. Ako ne mora biti n € |N, onda je rjesenje i n = -1... Smile



_________________
U pravilu ignoriram pitanja u krivim topicima i kodove koji nisu u [code]...[/code] blokovima.
Takodjer, OBJASNITE sto vas muci! "Sto mi je krivo?", bez opisa u cemu je problem, rijetko ce zadobiti moju paznju. Drzim prodike
[Vrh]
Korisnički profil Pošaljite privatnu poruku
2HigH
Gost
PostPostano: 21:20 sri, 19. 10. 2005    Naslov: Citirajte i odgovorite
E puno hvala. Al meni ne treba rješenje koliko je n nego je to zapravo MATEMATIČKA INDUKCIJA!

Cijeli zadatak ti glasi ovako:
[URL=http://imageshack.us][img]http://img444.imageshack.us/img444/4170/zadatak6oe.png[/img][/URL]

Za prvi slučaj dobio sam da za n=1 vrijedi.
Za drugi slučaj pretpostavimo da vrijedi kako piše zadatak.
A sad za treći slučaj treba dokraja dogurat, a to neznam. Znači treći slučaj T(n)->T(n+1). Kad se to sve sredi, dođem do onog koraka koji je gore naveden i dalje neznam. Treba dobit da je jedna i druga strana ista ili 0=0!
E puno hvala. Al meni ne treba rješenje koliko je n nego je to zapravo MATEMATIČKA INDUKCIJA!

Cijeli zadatak ti glasi ovako:


Za prvi slučaj dobio sam da za n=1 vrijedi.
Za drugi slučaj pretpostavimo da vrijedi kako piše zadatak.
A sad za treći slučaj treba dokraja dogurat, a to neznam. Znači treći slučaj T(n)->T(n+1). Kad se to sve sredi, dođem do onog koraka koji je gore naveden i dalje neznam. Treba dobit da je jedna i druga strana ista ili 0=0!


[Vrh]
vsego
Site Admin
Site Admin


Pridružen/a: 06. 10. 2002. (22:07:09)
Postovi: (3560)16
Spol: zombi
Sarma = la pohva - posuda
854 = 1068 - 214
Lokacija: /sbin/init
PostPostano: 21:53 sri, 19. 10. 2005    Naslov: Citirajte i odgovorite
Pa, rijesio sam ti jednadzbu, dakle isto je za n = 1 ili n = -1. :-s Zvuci kao da si fulao u postupku... :?

Da vidimo za n+1:

[latex]$\begin{equation*}\begin{array}{l}
1\cdot 2^{n+1} + 2 \cdot 2^n + \ldots + (n+1) \cdot 2 + (n+2) = \\
\textrm{izlu\v{c}i 2 iz prvih $n+1$ pribrojnika} \\
2 \cdot (1\cdot 2^n + 2 \cdot 2^{n-1} + \ldots + (n+1)) + (n+2) = \\
\textrm{po pretpostavci indukcije} \\
2 \cdot (2^{n+2} - (n - 3)) + (n+2) = \\
2^{n+3} - 2n + 6 + n + 2 = \\
2^{n+3} - n + 8 = \\
2^{(n+1)+2} - ((n+1) - 3) + 6
\end{array}\end{equation*}$[/latex]

Meni se cini da to ne vrijedi... :?

[code:1][vsego@degiorgi ~]$ perl -e 'foreach$n(1..10){$s=0;foreach(0..$n){$s+=($_+1)*2**($n-$_);}print$n,": ",$s," ? ",2**($n+2)-($n-3),"\n";}'
1: 4 ? 10
2: 11 ? 17
3: 26 ? 32
4: 57 ? 63
5: 120 ? 126
6: 247 ? 253
7: 502 ? 508
8: 1013 ? 1019
9: 2036 ? 2042
10: 4083 ? 4089
[vsego@degiorgi ~]$ perl -e 'foreach$n(1..10){$s=0;foreach(0..$n){$s+=($_+1)*2**($n-$_);}print$n,": ",$s," ? ",2**($n+2)-($n+3),"\n";}'
1: 4 ? 4
2: 11 ? 11
3: 26 ? 26
4: 57 ? 57
5: 120 ? 120
6: 247 ? 247
7: 502 ? 502
8: 1013 ? 1013
9: 2036 ? 2036
10: 4083 ? 4083[/code:1]

Fulao si: u zadnjoj zagradi je "+3". :D Sad provedi kako sam opisao za "-3" i bit ce u redu... 8)

P.S. Please, manje scannove ubuduce. :)
Pa, rijesio sam ti jednadzbu, dakle isto je za n = 1 ili n = -1. Eh? Zvuci kao da si fulao u postupku... Confused

Da vidimo za n+1:



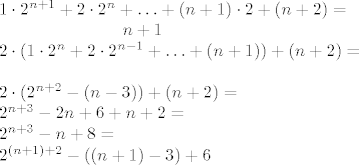
Meni se cini da to ne vrijedi... Confused

Kod:
[vsego@degiorgi ~]$ perl -e 'foreach$n(1..10){$s=0;foreach(0..$n){$s+=($_+1)*2**($n-$_);}print$n,": ",$s," ? ",2**($n+2)-($n-3),"\n";}'
1: 4 ? 10
2: 11 ? 17
3: 26 ? 32
4: 57 ? 63
5: 120 ? 126
6: 247 ? 253
7: 502 ? 508
8: 1013 ? 1019
9: 2036 ? 2042
10: 4083 ? 4089
[vsego@degiorgi ~]$ perl -e 'foreach$n(1..10){$s=0;foreach(0..$n){$s+=($_+1)*2**($n-$_);}print$n,": ",$s," ? ",2**($n+2)-($n+3),"\n";}'
1: 4 ? 4
2: 11 ? 11
3: 26 ? 26
4: 57 ? 57
5: 120 ? 120
6: 247 ? 247
7: 502 ? 502
8: 1013 ? 1013
9: 2036 ? 2036
10: 4083 ? 4083


Fulao si: u zadnjoj zagradi je "+3". Very Happy Sad provedi kako sam opisao za "-3" i bit ce u redu... Cool

P.S. Please, manje scannove ubuduce. Smile



_________________
U pravilu ignoriram pitanja u krivim topicima i kodove koji nisu u [code]...[/code] blokovima.
Takodjer, OBJASNITE sto vas muci! "Sto mi je krivo?", bez opisa u cemu je problem, rijetko ce zadobiti moju paznju. Drzim prodike
[Vrh]
Korisnički profil Pošaljite privatnu poruku
2HigH
Gost
PostPostano: 23:20 sri, 19. 10. 2005    Naslov: Citirajte i odgovorite
Hvala puno. Dužan sam ti! 8)
Hvala puno. Dužan sam ti! Cool


[Vrh]
Prethodni postovi:   
Započnite novu temu   Odgovorite na temu   printer-friendly view    Forum@DeGiorgi: Početna -> Ostalo - ozbiljno -> Čistilište Vremenska zona: GMT + 01:00.
Stranica 1 / 1.

 
Forum(o)Bir:  
Ne možete otvarati nove teme.
Ne možete odgovarati na postove.
Ne možete uređivati Vaše postove.
Ne možete izbrisati Vaše postove.
Ne možete glasovati u anketama.
You can attach files in this forum
You can download files in this forum


Powered by phpBB © 2001, 2002 phpBB Group
Theme created by Vjacheslav Trushkin
HR (Cro) by Ančica Sečan