|
[quote="pefri"][b]Da li je d metrika?
d(m,n) = { 0, m = n
3^(-k), m-n = 3^k *l, l nije djeljiv s 3[/b][/quote]
[quote="pefri"]M4) d(m,n) <= d(m,p) + d(p,n)
Kako za sva tri m,n i p različita?[/quote]
Neka je [latex]m-p=3^a\cdot u,\ p-n=3^b\cdot v[/latex]
Pretpostavimo recimo da je a<=b. (Analogno za a>=b.)
Tada je [latex]m-n=(m-p)+(p-n)=3^a\cdot(u+3^{b-a}\cdot v)[/latex] pa je eksponent u najvećoj potenciji od 3 koja dijeli m-n veći ili jednak a.
[latex]d(m,n)\leq 3^{-a} \leq 3^{-a}+3^{-b}=d(m,p)+d(p,n)[/latex]
[quote="pefri"][b]d(x,y)=|x-y|-e^(-|x-y|)+1 je metrika. Da li je ultrametrika?[/b]
d(x,y) <= max{d(x,z),d(z,y)}[/quote]
[quote="pefri"]za x=y trivijalno vrijedi
u slučaju x,y,z međusobno različiti d(x,y) <= d(x,z) + d(z,y) <= 2* max{ d(x,z), d(z,y)} odakle naslućujem da nije ultrametrika pa protuprimjerom pokažem npr. za x=1 y=5 i z=3 da ne vrijedi nejednakost d(x,y) <= max{d(x,z),d(z,y)}. DA li je dobar ovakav postupak?[/quote]
Da. x=1, y=5 i z=3 je dobar protuprimjer.
| pefri (napisa): | Da li je d metrika?
d(m,n) = { 0, m = n
3^(-k), m-n = 3^k *l, l nije djeljiv s 3 |
| pefri (napisa): | M4) d(m,n) ⇐ d(m,p) + d(p,n)
Kako za sva tri m,n i p različita? |
Neka je 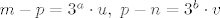
Pretpostavimo recimo da je a⇐b. (Analogno za a>=b.)
Tada je  pa je eksponent u najvećoj potenciji od 3 koja dijeli m-n veći ili jednak a. pa je eksponent u najvećoj potenciji od 3 koja dijeli m-n veći ili jednak a.
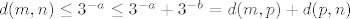
| pefri (napisa): | d(x,y)=|x-y|-e^(-|x-y|)+1 je metrika. Da li je ultrametrika?
d(x,y) ⇐ max{d(x,z),d(z,y)} |
| pefri (napisa): | za x=y trivijalno vrijedi
u slučaju x,y,z međusobno različiti d(x,y) ⇐ d(x,z) + d(z,y) ⇐ 2* max{ d(x,z), d(z,y)} odakle naslućujem da nije ultrametrika pa protuprimjerom pokažem npr. za x=1 y=5 i z=3 da ne vrijedi nejednakost d(x,y) ⇐ max{d(x,z),d(z,y)}. DA li je dobar ovakav postupak? |
Da. x=1, y=5 i z=3 je dobar protuprimjer.
|




