| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
Gost
|
|
| [Vrh] |
|
goranm
Forumaš(ica)


Pridružen/a: 12. 11. 2002. (20:09:12)
Postovi: (906)16
Spol: 
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
hermione
Forumaš(ica)


Pridružen/a: 23. 09. 2003. (10:50:57)
Postovi: (152)16
Spol: 
Sarma: -
|
|
| [Vrh] |
|
goranm
Forumaš(ica)


Pridružen/a: 12. 11. 2002. (20:09:12)
Postovi: (906)16
Spol: 
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
hermione
Forumaš(ica)


Pridružen/a: 23. 09. 2003. (10:50:57)
Postovi: (152)16
Spol: 
Sarma: -
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
amimica
Forumaš(ica)

Pridružen/a: 14. 04. 2004. (15:40:42)
Postovi: (CA)16
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
Gost
|
 Postano: 13:50 sri, 26. 4. 2006 Naslov: Postano: 13:50 sri, 26. 4. 2006 Naslov: |
    |
|
|
Jel netko uspio rjesiti 3zadatak pod c?
Iz segmenta [0,1] na slucajan nacin i nezavisno biramo tocke x,y,z. Izr vjer da vrijedi 2xy >= zx + zy.
(dosao sam do integrala, no tamo sam zapeo... :oops: )
A zadatak 9?
Na kruznici polumjera R se slucajno biraju dvije tocke. Kolika je vjerojatnost da ce udaljenost medju njima biti manja od r, gdje je r<2R?
Jel netko uspio rjesiti 3zadatak pod c?
Iz segmenta [0,1] na slucajan nacin i nezavisno biramo tocke x,y,z. Izr vjer da vrijedi 2xy >= zx + zy.
(dosao sam do integrala, no tamo sam zapeo...  ) )
A zadatak 9?
Na kruznici polumjera R se slucajno biraju dvije tocke. Kolika je vjerojatnost da ce udaljenost medju njima biti manja od r, gdje je r<2R?
|
|
| [Vrh] |
|
greeneyes
Forumaš(ica)


Pridružen/a: 13. 09. 2004. (11:44:20)
Postovi: (CD)16
Spol: 
Lokacija: The water's edge Is where she waits
|
 Postano: 15:16 sri, 26. 4. 2006 Naslov: Postano: 15:16 sri, 26. 4. 2006 Naslov: |
    |
|
|
za ovo prvo.. imas dvostruki integral (granice svakog su od nula do jedan) od 2xy/(x+y) jel da? pa to malo sredis i dobis 3 jednostruka po y, od cega je jedan skroz ok ( integriras 2y u granicama nula do jedan), i imas integral od -2y^2*ln(1+y) i 2y^2lny (opet, granice su od nula do jedan).. ova dva zadnja lijepo rijesis parcijalnom integracijom (u=ln(1+y), i u drugom slucaju u=lny).. mislim, ima nest malo raspisivanja al dodje dobro na kraju.. rezultat je 4/3(1-ln2).. znam da je ovo ljepse (i citljivije ;O) ) vidjeti onak lijepo s integralima i svim, but this is the best i can do at the moment..
a drugo.. nacrtas sliku, gledas, gledas.. pa uzmes formule za kruzni odsjecak i tam nadjes zgodnicku formulu da je udaljenost tih dviju tocki moguce odrediti iz formule d=2*R*sin(alfa/2), gdje je alfa sredisnji kut nad tom tetivom..
znaci, fixiras tocku na kruznici, i zapravo biras kut alfa iz [0, pi] (zato jer d mora biti manje od r, koje je manje od promjera (vidi opet promjer u igri :O) ) tj alfa je manje od pi..) i to ti je vj. prostor ( [0,pi])
A je dogadjaj da je d<r, podijelis s 2*R i dobis da sin(alfa/2)<r/(2*R)onda rjesenje te trigonometrijske nejednadzbe (alfa) ispadne iz intervala [0,2*Arcsin(r/(2*R))], pa znaci da je mjera od A duljina tog intervala, i to jos podijelis s pi (mjera od omega) i to je trazena vjerojatnost.. evo, otprilike :O)
nadam se da se da shvatiti.. heh :wink:
za ovo prvo.. imas dvostruki integral (granice svakog su od nula do jedan) od 2xy/(x+y) jel da? pa to malo sredis i dobis 3 jednostruka po y, od cega je jedan skroz ok ( integriras 2y u granicama nula do jedan), i imas integral od -2y^2*ln(1+y) i 2y^2lny (opet, granice su od nula do jedan).. ova dva zadnja lijepo rijesis parcijalnom integracijom (u=ln(1+y), i u drugom slucaju u=lny).. mislim, ima nest malo raspisivanja al dodje dobro na kraju.. rezultat je 4/3(1-ln2).. znam da je ovo ljepse (i citljivije ;O) ) vidjeti onak lijepo s integralima i svim, but this is the best i can do at the moment..
a drugo.. nacrtas sliku, gledas, gledas.. pa uzmes formule za kruzni odsjecak i tam nadjes zgodnicku formulu da je udaljenost tih dviju tocki moguce odrediti iz formule d=2*R*sin(alfa/2), gdje je alfa sredisnji kut nad tom tetivom..
znaci, fixiras tocku na kruznici, i zapravo biras kut alfa iz [0, pi] (zato jer d mora biti manje od r, koje je manje od promjera (vidi opet promjer u igri :O) ) tj alfa je manje od pi..) i to ti je vj. prostor ( [0,pi])
A je dogadjaj da je d<r, podijelis s 2*R i dobis da sin(alfa/2)<r/(2*R)onda rjesenje te trigonometrijske nejednadzbe (alfa) ispadne iz intervala [0,2*Arcsin(r/(2*R))], pa znaci da je mjera od A duljina tog intervala, i to jos podijelis s pi (mjera od omega) i to je trazena vjerojatnost.. evo, otprilike :O)
nadam se da se da shvatiti.. heh 
_________________
Am I so different from you
Now does it scare you that I'm able to discern
What to love and what to burn..
Don't judge what you don't understand..
// Disturbed: Fear
|
|
| [Vrh] |
|
hermione
Forumaš(ica)


Pridružen/a: 23. 09. 2003. (10:50:57)
Postovi: (152)16
Spol: 
Sarma: -
|
 Postano: 16:09 sri, 26. 4. 2006 Naslov: Postano: 16:09 sri, 26. 4. 2006 Naslov: |
    |
|
|
[quote="Anonymous"]Jel netko uspio rjesiti 3zadatak pod c?
Iz segmenta [0,1] na slucajan nacin i nezavisno biramo tocke x,y,z. Izr vjer da vrijedi 2xy >= zx + zy.
(dosao sam do integrala, no tamo sam zapeo... :oops: )
[/quote]
[latex]
\int_{0}^{1}\int_{0}^{1}\frac{2xy}{x+y} \,dy\,dx = \int_{0}^{1}\int_{0}^{1} \frac {2xy + 2y^2 - 2y^2}{x+y} \,dy\,dx =
\int_{0}^{1}\int_{0}^{1}\frac{2y\left(x+y\right)-2y^2}{x+y} \,dy\,dx \\=
\int_{0}^{1}\int_{0}^{1} 2y- \frac{2y^2}{x+y}\,dy\,dx =
\int_{0}^{1}\int_{0}^{1}2y \,dy\,dx -2\int_{0}^{1}\int_{0}^{1}\frac{y^2}{x+y}\,dy\,dx=\dots =\frac{4}{3}\left(1-ln2\right)
[/latex]
| Anonymous (napisa): | Jel netko uspio rjesiti 3zadatak pod c?
Iz segmenta [0,1] na slucajan nacin i nezavisno biramo tocke x,y,z. Izr vjer da vrijedi 2xy >= zx + zy.
(dosao sam do integrala, no tamo sam zapeo...  ) )
|
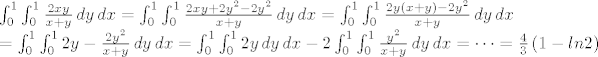
|
|
| [Vrh] |
|
hermione
Forumaš(ica)


Pridružen/a: 23. 09. 2003. (10:50:57)
Postovi: (152)16
Spol: 
Sarma: -
|
 Postano: 17:40 sri, 26. 4. 2006 Naslov: Postano: 17:40 sri, 26. 4. 2006 Naslov: |
    |
|
|
[quote="Anonymous"]
A zadatak 9?
Na kruznici polumjera R se slucajno biraju dvije tocke. Kolika je vjerojatnost da ce udaljenost medju njima biti manja od r, gdje je r<2R?[/quote]
Moze i ovako. Izaberemo dvije tocke na kruznici koje zajedno sa sredistem kruznice cine trokut.Osnovica tog trokuta je d, tj udaljenost izmedu nase dvije proizvoljne dvije tocke, a φ/2 je kut izmedu radijusa kruznice i visine na osnovicu.
[latex]
d = 2R\sin\frac{\varphi}{2}<r \Longleftrightarrow
\sin\frac{\varphi}{2}<\frac{r}{2R}
\Longleftrightarrow\frac{\varphi}{2}<\arcsin\frac{r}{2R}\Longleftrightarrow
\varphi<2\arcsin\frac{r}{2R}
\\|\varphi_{1}-\varphi_{2}|<2\arcsin\frac{r}{2R}, \quad
|\varphi_{1}-\varphi_{2}\pm 2\pi|<2\arcsin\frac{r}{2R},\ {a}
\quad\Omega=[0,2\pi]\times [0,2\pi] \\
P=\frac{{4\arcsin\frac{r}{2R}\cdot2\pi}}{\left({2\pi}\right)^2}=
\frac{2}{\pi}\arcsin\frac{r}{2R}
[/latex]
| Anonymous (napisa): |
A zadatak 9?
Na kruznici polumjera R se slucajno biraju dvije tocke. Kolika je vjerojatnost da ce udaljenost medju njima biti manja od r, gdje je r<2R? |
Moze i ovako. Izaberemo dvije tocke na kruznici koje zajedno sa sredistem kruznice cine trokut.Osnovica tog trokuta je d, tj udaljenost izmedu nase dvije proizvoljne dvije tocke, a φ/2 je kut izmedu radijusa kruznice i visine na osnovicu.
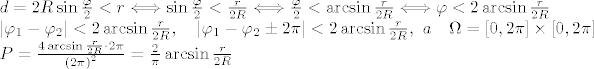
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
hermione
Forumaš(ica)


Pridružen/a: 23. 09. 2003. (10:50:57)
Postovi: (152)16
Spol: 
Sarma: -
|
|
| [Vrh] |
|
Nikola
Gost
|
|
| [Vrh] |
|
Gost
|
 Postano: 0:49 uto, 2. 5. 2006 Naslov: Postano: 0:49 uto, 2. 5. 2006 Naslov: |
    |
|
|
[quote="hermione"][quote="Anonymous"]
A zadatak 9?
Na kruznici polumjera R se slucajno biraju dvije tocke. Kolika je vjerojatnost da ce udaljenost medju njima biti manja od r, gdje je r<2R?[/quote]
Moze i ovako. Izaberemo dvije tocke na kruznici koje zajedno sa sredistem kruznice cine trokut.Osnovica tog trokuta je d, tj udaljenost izmedu nase dvije proizvoljne dvije tocke, a φ/2 je kut izmedu radijusa kruznice i visine na osnovicu.
[latex]
d = 2R\sin\frac{\varphi}{2}<r \Longleftrightarrow
\sin\frac{\varphi}{2}<\frac{r}{2R}
\Longleftrightarrow\frac{\varphi}{2}<\arcsin\frac{r}{2R}\Longleftrightarrow
\varphi<2\arcsin\frac{r}{2R}
\\|\varphi_{1}-\varphi_{2}|<2\arcsin\frac{r}{2R}, \quad
|\varphi_{1}-\varphi_{2}\pm 2\pi|<2\arcsin\frac{r}{2R},\ {a}
\quad\Omega=[0,2\pi]\times [0,2\pi] \\
P=\frac{{4\arcsin\frac{r}{2R}\cdot2\pi}}{\left({2\pi}\right)^2}=
\frac{2}{\pi}\arcsin\frac{r}{2R}
[/latex][/quote]
Što su fi_1 i fi_2 i zasto apsolutna vrijednost? Kako dobijemo brojnik od P? Thx!
| hermione (napisa): | | Anonymous (napisa): |
A zadatak 9?
Na kruznici polumjera R se slucajno biraju dvije tocke. Kolika je vjerojatnost da ce udaljenost medju njima biti manja od r, gdje je r<2R? |
Moze i ovako. Izaberemo dvije tocke na kruznici koje zajedno sa sredistem kruznice cine trokut.Osnovica tog trokuta je d, tj udaljenost izmedu nase dvije proizvoljne dvije tocke, a φ/2 je kut izmedu radijusa kruznice i visine na osnovicu.
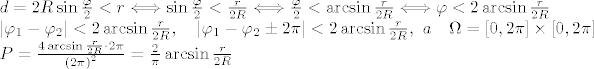 |
Što su fi_1 i fi_2 i zasto apsolutna vrijednost? Kako dobijemo brojnik od P? Thx!
|
|
| [Vrh] |
|
Gost
|
 Postano: 2:53 uto, 2. 5. 2006 Naslov: Postano: 2:53 uto, 2. 5. 2006 Naslov: |
    |
|
|
Može li mi netko rijesiti ovaj zadatak:
Biramo tri dužine čije su duljine na sreću odabrani brojevi iz intervala [0,a]. Kolika je vjerojatnost da se od tih dijelova može napraviti trokut?
Znam početak :D :
x, y, z €[0.a] => omega=[0,a]^3 => m(omega)=a^3
Mora biti: x+y>z, x+z>y, y+z>x ili x<a/2, y<a/2, z<a/2.
Kako dalje? Vidjela sam u riješenjima da ide nešto sa volumenima 3 tetraedra, ali ne kužim.
Puno hvala! :-)
Može li mi netko rijesiti ovaj zadatak:
Biramo tri dužine čije su duljine na sreću odabrani brojevi iz intervala [0,a]. Kolika je vjerojatnost da se od tih dijelova može napraviti trokut?
Znam početak  : :
x, y, z €[0.a] ⇒ omega=[0,a]^3 ⇒ m(omega)=a^3
Mora biti: x+y>z, x+z>y, y+z>x ili x<a/2, y<a/2, z<a/2.
Kako dalje? Vidjela sam u riješenjima da ide nešto sa volumenima 3 tetraedra, ali ne kužim.
Puno hvala! 
|
|
| [Vrh] |
|
|












