| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
goranm
Forumaš(ica)


Pridružen/a: 12. 11. 2002. (20:09:12)
Postovi: (906)16
Spol: 
|
|
| [Vrh] |
|
Ignavia
Forumaš(ica)


Pridružen/a: 02. 10. 2004. (19:22:39)
Postovi: (235)16
Spol: 
Lokacija: prijestolnica
|
|
| [Vrh] |
|
Ilja
Forumaš(ica)

Pridružen/a: 30. 10. 2002. (22:22:31)
Postovi: (1AF)16
|
 Postano: 21:32 pet, 30. 6. 2006 Naslov: Re: Ocjena pogreške splajna 1. stupnja Postano: 21:32 pet, 30. 6. 2006 Naslov: Re: Ocjena pogreške splajna 1. stupnja |
    |
|
|
[quote="Ignavia"][quote="goranm"]Zašto vrijedi:
Ako je [latex]x \in [a,b][/latex] onda postoji [latex]i \in \{0,1,\dots,n-1\}[/latex] tako da vrijedi:
[latex]f(x)-L_1f(x)=\frac{1}{2}f^{''}(\zeta)(x-x_i)(x-x_{i+1}),\quad \zeta \in [x_i,x_{i+1}]\subseteq[a,b][/latex][/quote]
TAKO JE! zasto to vrijedi? :D[/quote]
Pa to slijedi iz izvoda ocjene pogreške za interpolaciju prvog stupnja.
Spline je po dijelovima linearna interpolacija prvog supnja, pa na podsegmentima na kojima je linearna možemo koristiti izvod za ocjenu pogreške interpolacije polinomom (u ovom slučaju prvog stupnja). :D
@Ignavia: :cmok: :oops:
| Ignavia (napisa): | | goranm (napisa): | Zašto vrijedi:
Ako je 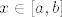 onda postoji onda postoji  tako da vrijedi: tako da vrijedi:
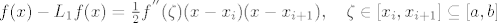 |
TAKO JE! zasto to vrijedi?  |
Pa to slijedi iz izvoda ocjene pogreške za interpolaciju prvog stupnja.
Spline je po dijelovima linearna interpolacija prvog supnja, pa na podsegmentima na kojima je linearna možemo koristiti izvod za ocjenu pogreške interpolacije polinomom (u ovom slučaju prvog stupnja). 
@Ignavia:  
|
|
| [Vrh] |
|
Ignavia
Forumaš(ica)


Pridružen/a: 02. 10. 2004. (19:22:39)
Postovi: (235)16
Spol: 
Lokacija: prijestolnica
|
|
| [Vrh] |
|
MB
Forumaš(ica)


Pridružen/a: 01. 07. 2005. (12:35:21)
Postovi: (224)16
Spol: 
Lokacija: Molvice
|
|
| [Vrh] |
|
zavod za analizu
Forumaš s poteškoćama u pisanju

Pridružen/a: 23. 06. 2006. (05:33:55)
Postovi: (5A)16
Spol: 
|
 Postano: 10:12 sub, 1. 7. 2006 Naslov: Postano: 10:12 sub, 1. 7. 2006 Naslov: |
    |
|
|
[quote="MB"]meni to izgleda kao taylorov polinom srednje vrijednosti, sto je isti argument, valjda se tako dobiva i spomenuta ocjena 8)[/quote]
Taylorov teorem srednje vrijednosti je specijalni slučaj interpolacije u [u]samo jednoj točki[/u].
Ocjena za pogrešku interpolacije polinomom u točkama [latex]x_1,x_2,\ldots,x_r[/latex] i to ako u točki [latex]x_i[/latex] gledamo podudaranje prvih [latex]n_i[/latex] derivacija funkcije [i]f[/i] i polinoma [i]P[/i] glasi
[latex]\displaystyle f(x)-P(x)=\frac{f^{n+1}(\xi)}{(n+1)!}(x-x_1)^{n_1}(x-x_2)^{n_2} \ldots(x-x_r)^{n_r}[/latex]
za neku međutočku [latex]\xi[/latex] te uz pokratu [latex]n=n_1+n_2+\ldots n_r[/latex].
________
@MB: Kolega MB, malo smo razočarani. :vatrica:
@Ignavia: Evo, cijeli Zavod ti šalje: :cmok: :luck: :srce: :paprika:
| MB (napisa): | meni to izgleda kao taylorov polinom srednje vrijednosti, sto je isti argument, valjda se tako dobiva i spomenuta ocjena  |
Taylorov teorem srednje vrijednosti je specijalni slučaj interpolacije u samo jednoj točki.
Ocjena za pogrešku interpolacije polinomom u točkama 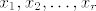 i to ako u točki i to ako u točki 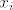 gledamo podudaranje prvih gledamo podudaranje prvih 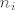 derivacija funkcije f i polinoma P glasi derivacija funkcije f i polinoma P glasi
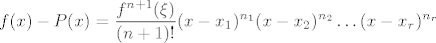
za neku međutočku 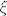 te uz pokratu te uz pokratu 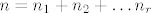 . .
________
@MB: Kolega MB, malo smo razočarani. 
@Ignavia: Evo, cijeli Zavod ti šalje:    
_________________  |
|
| [Vrh] |
|
Ignavia
Forumaš(ica)


Pridružen/a: 02. 10. 2004. (19:22:39)
Postovi: (235)16
Spol: 
Lokacija: prijestolnica
|
 Postano: 13:43 sub, 1. 7. 2006 Naslov: Postano: 13:43 sub, 1. 7. 2006 Naslov: |
    |
|
|
@zavod: hvala, paprika mi nedostaje vec tri dana... :tomato:
i evo jos malo pitanja za zavod pa i sire...
1. kod parcijalnog i potpunog pivotiranja smo napisali da nije potrebno izvrsiti zamjene redaka odnosno stupaca, nego samo pronadjemo doticni element u matrici s kojim hocemo ponistavat i onda bla bla...
hm, znaci dobijemo na kraju neku rupicastu matricu i da li nam je to sad neki problem? hocemo ju onda na kraju pretvorit u prekrasnu gornjetrokutastu ili nas to uopce ne zanima? ako ne, onda ce kompic stalno morat provjeravat i trazit di je nula di ne (kad rjesava sustav)? dal mi mozda nismo uopce obzirni prema kompicu? :cry:
2. dobili smo jednom za dz usporedit ocjenu pogreske kod Taylorovog i interpolacijskog polinoma u nultockama Cebisevljevog p., kak to tocno trebamo napravit - jasno je npr da kod interpol. imamo maksimum n+1-ve derivacije(tj. u nekoj tocki isto, al si malo zaokruzimo), a kod T. n+1-vu u nekoj tocki, (n+1)! i kod jednog i kod drugog, ali kaj cemo s ostatkom...
3. ona tri teorem- Faber, 2. i Weierstrass koje smo samo naveli trebaju i ostat samo navedeni il kaj? (dokaz?) (ovo je podmetnuto glupo pitanje)
4. kakvu posebnu poruku nam salje Rungeov primjer? (u smislu Pn ne tezi ka f(x))
f(x)=1/1+x^2
5. sto je s Banachovim milim teoremom, pa to je najsvjetlija tocka, a nismo ni spomenuli na predavanjima? jel smo to mozda kojim slucajem dobili za zadacu bez da sam ja toga svijesna ili ne? opcenito rjesavanja nelinearnih jednadzbi ima samo 2 lista???
:band:
@zavod: hvala, paprika mi nedostaje vec tri dana... 
i evo jos malo pitanja za zavod pa i sire...
1. kod parcijalnog i potpunog pivotiranja smo napisali da nije potrebno izvrsiti zamjene redaka odnosno stupaca, nego samo pronadjemo doticni element u matrici s kojim hocemo ponistavat i onda bla bla...
hm, znaci dobijemo na kraju neku rupicastu matricu i da li nam je to sad neki problem? hocemo ju onda na kraju pretvorit u prekrasnu gornjetrokutastu ili nas to uopce ne zanima? ako ne, onda ce kompic stalno morat provjeravat i trazit di je nula di ne (kad rjesava sustav)? dal mi mozda nismo uopce obzirni prema kompicu? 
2. dobili smo jednom za dz usporedit ocjenu pogreske kod Taylorovog i interpolacijskog polinoma u nultockama Cebisevljevog p., kak to tocno trebamo napravit - jasno je npr da kod interpol. imamo maksimum n+1-ve derivacije(tj. u nekoj tocki isto, al si malo zaokruzimo), a kod T. n+1-vu u nekoj tocki, (n+1)! i kod jednog i kod drugog, ali kaj cemo s ostatkom...
3. ona tri teorem- Faber, 2. i Weierstrass koje smo samo naveli trebaju i ostat samo navedeni il kaj? (dokaz?) (ovo je podmetnuto glupo pitanje)
4. kakvu posebnu poruku nam salje Rungeov primjer? (u smislu Pn ne tezi ka f(x))
f(x)=1/1+x^2
5. sto je s Banachovim milim teoremom, pa to je najsvjetlija tocka, a nismo ni spomenuli na predavanjima? jel smo to mozda kojim slucajem dobili za zadacu bez da sam ja toga svijesna ili ne? opcenito rjesavanja nelinearnih jednadzbi ima samo 2 lista???
|
|
| [Vrh] |
|
Anđelčić
Forumaš(ica)

Pridružen/a: 11. 05. 2005. (16:57:50)
Postovi: (201)16
|
 Postano: 14:12 sub, 1. 7. 2006 Naslov: Postano: 14:12 sub, 1. 7. 2006 Naslov: |
    |
|
|
evo, ja cu odgovorit na jedno, a nek si ovi iz zavoda rasporede ostala 4 :)
[quote="Ignavia"]
5. sto je s Banachovim milim teoremom, pa to je najsvjetlija tocka, a nismo ni spomenuli na predavanjima? jel smo to mozda kojim slucajem dobili za zadacu bez da sam ja toga svijesna ili ne? opcenito rjesavanja nelinearnih jednadzbi ima samo 2 lista???
[/quote]
radili smo banacha zadnji sat, kao secer na kraju :)
ima koji list vise nelinearnih :)
evo, ja cu odgovorit na jedno, a nek si ovi iz zavoda rasporede ostala 4 
| Ignavia (napisa): |
5. sto je s Banachovim milim teoremom, pa to je najsvjetlija tocka, a nismo ni spomenuli na predavanjima? jel smo to mozda kojim slucajem dobili za zadacu bez da sam ja toga svijesna ili ne? opcenito rjesavanja nelinearnih jednadzbi ima samo 2 lista???
|
radili smo banacha zadnji sat, kao secer na kraju 
ima koji list vise nelinearnih 
|
|
| [Vrh] |
|
Ignavia
Forumaš(ica)


Pridružen/a: 02. 10. 2004. (19:22:39)
Postovi: (235)16
Spol: 
Lokacija: prijestolnica
|
|
| [Vrh] |
|
Anđelčić
Forumaš(ica)

Pridružen/a: 11. 05. 2005. (16:57:50)
Postovi: (201)16
|
|
| [Vrh] |
|
Ignavia
Forumaš(ica)


Pridružen/a: 02. 10. 2004. (19:22:39)
Postovi: (235)16
Spol: 
Lokacija: prijestolnica
|
|
| [Vrh] |
|
vsego
Site Admin


Pridružen/a: 06. 10. 2002. (22:07:09)
Postovi: (3562)16
Spol: 
Lokacija: /sbin/init
|
|
| [Vrh] |
|
Anđelčić
Forumaš(ica)

Pridružen/a: 11. 05. 2005. (16:57:50)
Postovi: (201)16
|
|
| [Vrh] |
|
Ignavia
Forumaš(ica)


Pridružen/a: 02. 10. 2004. (19:22:39)
Postovi: (235)16
Spol: 
Lokacija: prijestolnica
|
|
| [Vrh] |
|
Anđelčić
Forumaš(ica)

Pridružen/a: 11. 05. 2005. (16:57:50)
Postovi: (201)16
|
|
| [Vrh] |
|
goranm
Forumaš(ica)


Pridružen/a: 12. 11. 2002. (20:09:12)
Postovi: (906)16
Spol: 
|
|
| [Vrh] |
|
Anđelčić
Forumaš(ica)

Pridružen/a: 11. 05. 2005. (16:57:50)
Postovi: (201)16
|
|
| [Vrh] |
|
goranm
Forumaš(ica)


Pridružen/a: 12. 11. 2002. (20:09:12)
Postovi: (906)16
Spol: 
|
|
| [Vrh] |
|
Anđelčić
Forumaš(ica)

Pridružen/a: 11. 05. 2005. (16:57:50)
Postovi: (201)16
|
|
| [Vrh] |
|
goranm
Forumaš(ica)


Pridružen/a: 12. 11. 2002. (20:09:12)
Postovi: (906)16
Spol: 
|
|
| [Vrh] |
|
|

















