| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
Chvarak
Forumaš(ica)


Pridružen/a: 06. 12. 2006. (14:12:04)
Postovi: (12)16
Spol: 
|
 Postano: 0:33 ned, 18. 2. 2007 Naslov: Zadaci sa usmenog Postano: 0:33 ned, 18. 2. 2007 Naslov: Zadaci sa usmenog |
    |
|
|
[color=darkblue]Da li se moze naci neka dobra dusa da rijesi ovo:[/color]1.zadatak
Neka je V vektorski prostor i A = {a1, a2, a3, a4, a5} linearno zavisan skup vektorau V . Odredite koji od navedenih zakljuˇcaka se mogu izvesti:
(a) Postoji vektor u A koji je linearna kombinacija preostalih vektora iz A.
Da Ne
(b) A nije sustav izvodnica za V .
Da Ne
(c) Svaki vektor skupa A se moˇze prikazati kao linearna kombinacija preostalih
vektora iz A.
Da Ne
(d) dim[A] _ 5.
Da Ne
(e) Postoji vektor u A koji se moˇze prikazati kao linearna kombinacija svojih
prethodnika u A.
Da Ne
(f) Postoji linearno nezavisan podskup skupaA.
Da Ne
(g) Skup A se moˇze reducirati do baze prostora V .
2.zadatak:dokazi
1) za kvadratne matrice A i B,A regularna vrijedi:
det(A(na -1)*B*A)=DET(A*B*A(-1))
2)adjunkta gornjetrokutaste matrice A je donjetrokutasta
3)sustav lin jednadzbi sa n jednadzbi i n nepoznanica ima jedinstveno rjesenje
4)ako su A i B redcano ekvivalentne i A je invertibilna da li je i B
5)ako matrica ima sve lin nezavisne retke da li je regularna
6)u V ne postoji cetveroclani skup vektora takav da je svaki njegov troclani podskup lin nezavisan
7)ako A ima isti nulprostor kao i A(na T) onda matrica A mora biti kvadratna
Da li se moze naci neka dobra dusa da rijesi ovo:1.zadatak
Neka je V vektorski prostor i A = {a1, a2, a3, a4, a5} linearno zavisan skup vektorau V . Odredite koji od navedenih zakljuˇcaka se mogu izvesti:
(a) Postoji vektor u A koji je linearna kombinacija preostalih vektora iz A.
Da Ne
(b) A nije sustav izvodnica za V .
Da Ne
(c) Svaki vektor skupa A se moˇze prikazati kao linearna kombinacija preostalih
vektora iz A.
Da Ne
(d) dim[A] _ 5.
Da Ne
(e) Postoji vektor u A koji se moˇze prikazati kao linearna kombinacija svojih
prethodnika u A.
Da Ne
(f) Postoji linearno nezavisan podskup skupaA.
Da Ne
(g) Skup A se moˇze reducirati do baze prostora V .
2.zadatak:dokazi
1) za kvadratne matrice A i B,A regularna vrijedi:
det(A(na -1)*B*A)=DET(A*B*A(-1))
2)adjunkta gornjetrokutaste matrice A je donjetrokutasta
3)sustav lin jednadzbi sa n jednadzbi i n nepoznanica ima jedinstveno rjesenje
4)ako su A i B redcano ekvivalentne i A je invertibilna da li je i B
5)ako matrica ima sve lin nezavisne retke da li je regularna
6)u V ne postoji cetveroclani skup vektora takav da je svaki njegov troclani podskup lin nezavisan
7)ako A ima isti nulprostor kao i A(na T) onda matrica A mora biti kvadratna
_________________
...Visita Interiora Terrae Rectificando Invenies Occultum Lapidem...
|
|
| [Vrh] |
|
teja
Forumaš(ica)


Pridružen/a: 14. 07. 2006. (15:34:28)
Postovi: (14A)16
Spol: 
Lokacija: zg-ma and back
|
|
| [Vrh] |
|
Gost
|
 Postano: 11:44 ned, 18. 2. 2007 Naslov: Postano: 11:44 ned, 18. 2. 2007 Naslov: |
    |
|
|
U 1.f:
Ipak, postoji linearno nezavisan podskup tog skupa, za što je dovoljno da
postoji bar jedan vektor skupa različit od nulvektora. A čim je napisan skup od 5 elemenata, među njima ne može biti jednakih pa samo jedan može biti nulvektor.
2.4 : da, i B je regularna jer je istog tipa i ranga kao A
2.6. općenito ne postoji, npr. ako je dim V < 3.
2.7. da, očito, jer su tada stupci i retci jednake "duljine"
U 1.f:
Ipak, postoji linearno nezavisan podskup tog skupa, za što je dovoljno da
postoji bar jedan vektor skupa različit od nulvektora. A čim je napisan skup od 5 elemenata, među njima ne može biti jednakih pa samo jedan može biti nulvektor.
2.4 : da, i B je regularna jer je istog tipa i ranga kao A
2.6. općenito ne postoji, npr. ako je dim V < 3.
2.7. da, očito, jer su tada stupci i retci jednake "duljine"
|
|
| [Vrh] |
|
teja
Forumaš(ica)


Pridružen/a: 14. 07. 2006. (15:34:28)
Postovi: (14A)16
Spol: 
Lokacija: zg-ma and back
|
 Postano: 14:53 ned, 18. 2. 2007 Naslov: Postano: 14:53 ned, 18. 2. 2007 Naslov: |
    |
|
|
[quote="Anonymous"]U 1.f:
Ipak, postoji linearno nezavisan podskup tog skupa, za što je dovoljno da
postoji bar jedan vektor skupa različit od nulvektora. A čim je napisan skup od 5 elemenata, među njima ne može biti jednakih pa samo jedan može biti nulvektor.
[/quote]
a zašto ne može biti jednakih?
[quote="Anonymous"]
2.6. općenito ne postoji, npr. ako je dim V < 3.
[/quote]
hm.... tvrdnja je da ne postoji. dakle, ako može postojat onda tvrdnja nije točna.
| Anonymous (napisa): | U 1.f:
Ipak, postoji linearno nezavisan podskup tog skupa, za što je dovoljno da
postoji bar jedan vektor skupa različit od nulvektora. A čim je napisan skup od 5 elemenata, među njima ne može biti jednakih pa samo jedan može biti nulvektor.
|
a zašto ne može biti jednakih?
| Anonymous (napisa): |
2.6. općenito ne postoji, npr. ako je dim V < 3.
|
hm.... tvrdnja je da ne postoji. dakle, ako može postojat onda tvrdnja nije točna.
|
|
| [Vrh] |
|
herman
Forumaš(ica)

Pridružen/a: 07. 11. 2006. (19:51:13)
Postovi: (63)16
|
 Postano: 15:35 ned, 18. 2. 2007 Naslov: Postano: 15:35 ned, 18. 2. 2007 Naslov: |
    |
|
|
[quote="teja"][quote="Anonymous"]U 1.f:
Ipak, postoji linearno nezavisan podskup tog skupa, za što je dovoljno da
postoji bar jedan vektor skupa različit od nulvektora. A čim je napisan skup od 5 elemenata, među njima ne može biti jednakih pa samo jedan može biti nulvektor.
[/quote]
a zašto ne može biti jednakih?
Zato jer je {a, a, a, a, a} = {a}. :)
[quote="teja"] | Anonymous (napisa): | U 1.f:
Ipak, postoji linearno nezavisan podskup tog skupa, za što je dovoljno da
postoji bar jedan vektor skupa različit od nulvektora. A čim je napisan skup od 5 elemenata, među njima ne može biti jednakih pa samo jedan može biti nulvektor.
|
a zašto ne može biti jednakih?
Zato jer je {a, a, a, a, a} = {a}. 
|
|
| [Vrh] |
|
teja
Forumaš(ica)


Pridružen/a: 14. 07. 2006. (15:34:28)
Postovi: (14A)16
Spol: 
Lokacija: zg-ma and back
|
 Postano: 16:20 ned, 18. 2. 2007 Naslov: Postano: 16:20 ned, 18. 2. 2007 Naslov: |
    |
|
|
[quote="herman"][quote="teja"][quote="Anonymous"]U 1.f:
Ipak, postoji linearno nezavisan podskup tog skupa, za što je dovoljno da
postoji bar jedan vektor skupa različit od nulvektora. A čim je napisan skup od 5 elemenata, među njima ne može biti jednakih pa samo jedan može biti nulvektor.
[/quote]
a zašto ne može biti jednakih?
Zato jer je {a, a, a, a, a} = {a}. :)[/quote]
istina, ali odakle ti sigurnost da netko nije bio jako zao i mjesto {a} napisao {a,a,a,a,a}. ista stvar. :lol:
inače, ta da-ne pitanjca su uvijek jako diskutabilna....
[quote="herman"] | teja (napisa): | | Anonymous (napisa): | U 1.f:
Ipak, postoji linearno nezavisan podskup tog skupa, za što je dovoljno da
postoji bar jedan vektor skupa različit od nulvektora. A čim je napisan skup od 5 elemenata, među njima ne može biti jednakih pa samo jedan može biti nulvektor.
|
a zašto ne može biti jednakih?
Zato jer je {a, a, a, a, a} = {a}.  |
istina, ali odakle ti sigurnost da netko nije bio jako zao i mjesto {a} napisao {a,a,a,a,a}. ista stvar. 
inače, ta da-ne pitanjca su uvijek jako diskutabilna....
|
|
| [Vrh] |
|
goranm
Forumaš(ica)


Pridružen/a: 12. 11. 2002. (20:09:12)
Postovi: (906)16
Spol: 
|
|
| [Vrh] |
|
vsego
Site Admin


Pridružen/a: 06. 10. 2002. (22:07:09)
Postovi: (3562)16
Spol: 
Lokacija: /sbin/init
|
 Postano: 17:29 ned, 18. 2. 2007 Naslov: Re: Zadaci sa usmenog Postano: 17:29 ned, 18. 2. 2007 Naslov: Re: Zadaci sa usmenog |
    |
|
|
[quote="Chvarak"]1.zadatak
Neka je V vektorski prostor i A = {a1, a2, a3, a4, a5} linearno zavisan skup vektorau V . Odredite koji od navedenih zakljuˇcaka se mogu izvesti:
(e) Postoji vektor u A koji se moˇze prikazati kao linearna kombinacija svojih
prethodnika u A.
Da Ne[/quote]
Da. :) Prema (a), oko kojeg ste se slozili, postoji vektor koji je linearna kombinacija ostalih. 8) To zaci da postoje [latex]\alpha_i[/latex] koji nisu svi jednaki nuli, takvi da je [latex]\sum_i \alpha_i a_i = 0[/latex]. 8) Neka je [latex]k = \max \{i:\ \alpha_i \not= 0\}[/latex]. Tada je:
[latex]a_k = -\frac1{\alpha_k} \sum_{i<k} \alpha_i a_i[/latex]
| Chvarak (napisa): | 1.zadatak
Neka je V vektorski prostor i A = {a1, a2, a3, a4, a5} linearno zavisan skup vektorau V . Odredite koji od navedenih zakljuˇcaka se mogu izvesti:
(e) Postoji vektor u A koji se moˇze prikazati kao linearna kombinacija svojih
prethodnika u A.
Da Ne |
Da.  Prema (a), oko kojeg ste se slozili, postoji vektor koji je linearna kombinacija ostalih. Prema (a), oko kojeg ste se slozili, postoji vektor koji je linearna kombinacija ostalih.  To zaci da postoje To zaci da postoje 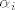 koji nisu svi jednaki nuli, takvi da je koji nisu svi jednaki nuli, takvi da je 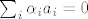 . .  Neka je Neka je 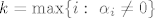 . Tada je: . Tada je:
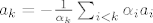
_________________ U pravilu ignoriram pitanja u krivim topicima i kodove koji nisu u [code]...[/code] blokovima.
Takodjer, OBJASNITE sto vas muci! "Sto mi je krivo?", bez opisa u cemu je problem, rijetko ce zadobiti moju paznju.  |
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
pinkgirl
Forumaš(ica)

Pridružen/a: 30. 11. 2006. (21:08:16)
Postovi: (1AE)16
Spol: 
Lokacija: K-K-Z
|
|
| [Vrh] |
|
vsego
Site Admin


Pridružen/a: 06. 10. 2002. (22:07:09)
Postovi: (3562)16
Spol: 
Lokacija: /sbin/init
|
 Postano: 18:06 ned, 18. 2. 2007 Naslov: Postano: 18:06 ned, 18. 2. 2007 Naslov: |
    |
|
|
[quote="Anonymous"]Odgovor je ne. Prvi vektor u skupu može biti nulvektor, a sljedeća 4 mogu činiti linearno nezavisan podskup. U tom slučaju skup je linearno zavisan, ali niti jedan vektor ne može se prikazati kao linearno kombinacije prethodnika.[/quote]
Hmda... u tom slucaju ovisi o tome da li mozemo reci da je nul-vektor linearna kombinacija prethodnika (tj. praznog skupa vektora, jer u sumi imamo i < 0). :| Ja sam pretpostavio da mozemo, jer on nema prethodnika, pa je linearna kombinacija "prazna", tj. njena suma je nul-vektor... :D
| Anonymous (napisa): | | Odgovor je ne. Prvi vektor u skupu može biti nulvektor, a sljedeća 4 mogu činiti linearno nezavisan podskup. U tom slučaju skup je linearno zavisan, ali niti jedan vektor ne može se prikazati kao linearno kombinacije prethodnika. |
Hmda... u tom slucaju ovisi o tome da li mozemo reci da je nul-vektor linearna kombinacija prethodnika (tj. praznog skupa vektora, jer u sumi imamo i < 0).  Ja sam pretpostavio da mozemo, jer on nema prethodnika, pa je linearna kombinacija "prazna", tj. njena suma je nul-vektor... Ja sam pretpostavio da mozemo, jer on nema prethodnika, pa je linearna kombinacija "prazna", tj. njena suma je nul-vektor... 
_________________ U pravilu ignoriram pitanja u krivim topicima i kodove koji nisu u [code]...[/code] blokovima.
Takodjer, OBJASNITE sto vas muci! "Sto mi je krivo?", bez opisa u cemu je problem, rijetko ce zadobiti moju paznju.  |
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
teja
Forumaš(ica)


Pridružen/a: 14. 07. 2006. (15:34:28)
Postovi: (14A)16
Spol: 
Lokacija: zg-ma and back
|
 Postano: 18:18 ned, 18. 2. 2007 Naslov: Postano: 18:18 ned, 18. 2. 2007 Naslov: |
    |
|
|
[quote="vsego"][quote="Anonymous"]Odgovor je ne. Prvi vektor u skupu može biti nulvektor, a sljedeća 4 mogu činiti linearno nezavisan podskup. U tom slučaju skup je linearno zavisan, ali niti jedan vektor ne može se prikazati kao linearno kombinacije prethodnika.[/quote]
Hmda... u tom slucaju ovisi o tome da li mozemo reci da je nul-vektor linearna kombinacija prethodnika (tj. praznog skupa vektora, jer u sumi imamo i < 0). :| Ja sam pretpostavio da mozemo, jer on nema prethodnika, pa je linearna kombinacija "prazna", tj. njena suma je nul-vektor... :D[/quote]
ma da :lol:
| vsego (napisa): | | Anonymous (napisa): | | Odgovor je ne. Prvi vektor u skupu može biti nulvektor, a sljedeća 4 mogu činiti linearno nezavisan podskup. U tom slučaju skup je linearno zavisan, ali niti jedan vektor ne može se prikazati kao linearno kombinacije prethodnika. |
Hmda... u tom slucaju ovisi o tome da li mozemo reci da je nul-vektor linearna kombinacija prethodnika (tj. praznog skupa vektora, jer u sumi imamo i < 0).  Ja sam pretpostavio da mozemo, jer on nema prethodnika, pa je linearna kombinacija "prazna", tj. njena suma je nul-vektor... Ja sam pretpostavio da mozemo, jer on nema prethodnika, pa je linearna kombinacija "prazna", tj. njena suma je nul-vektor...  |
ma da 
|
|
| [Vrh] |
|
herman
Forumaš(ica)

Pridružen/a: 07. 11. 2006. (19:51:13)
Postovi: (63)16
|
|
| [Vrh] |
|
|













