| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
Ilja
Forumaš(ica)
Pridružen/a: 30. 10. 2002. (22:22:31)
Postovi: (1AF)16
|
|
| [Vrh] |
|
vsego
Site Admin
Pridružen/a: 06. 10. 2002. (22:07:09)
Postovi: (3560)16
Spol: 
Lokacija: /sbin/init
|
|
| [Vrh] |
|
Ilja
Forumaš(ica)
Pridružen/a: 30. 10. 2002. (22:22:31)
Postovi: (1AF)16
|
|
| [Vrh] |
|
MB
Forumaš(ica)
Pridružen/a: 01. 07. 2005. (12:35:21)
Postovi: (224)16
Spol: 
Lokacija: Molvice
|
 Postano: 21:50 sri, 9. 5. 2007 Naslov: |
    |
|
|
evo glupavih pitanja nakon previse ucenja:
1. jel bitan clanak 'non-normal derivation...'?
2. jel se derivacija definira na komutativnoj algebri (pitam zbog Leibnitza)?
3. zasto stavljamo 'ogranicena' derivacija? jedino sto nam u tim zadacima treba je da je spektar ogranicen, a to imamo bez obzira kakav je operator, zar ne? ako se misli da je derivacija ogranicena kao lin. op., kud onda spada ona prica s kompaktnih op. kad smo pokazivali da u C([0,1]) derivacija nije neprekidna?
4. kak znamo da je bijekcija CH prostora homeomorfizam? pojavljuje se u nekom zadatku i na predavanjima..
Gelfandova se vise ne cini tak strasna, ali onaj primjer sa l^1(Z) je malo previse.. ne bih se nikad sjetio da iskoristim da je dual l^besk (iako se sjecam s kolokvija)
uglavnom, laku noc..
evo glupavih pitanja nakon previse ucenja:
1. jel bitan clanak 'non-normal derivation...'?
2. jel se derivacija definira na komutativnoj algebri (pitam zbog Leibnitza)?
3. zasto stavljamo 'ogranicena' derivacija? jedino sto nam u tim zadacima treba je da je spektar ogranicen, a to imamo bez obzira kakav je operator, zar ne? ako se misli da je derivacija ogranicena kao lin. op., kud onda spada ona prica s kompaktnih op. kad smo pokazivali da u C([0,1]) derivacija nije neprekidna?
4. kak znamo da je bijekcija CH prostora homeomorfizam? pojavljuje se u nekom zadatku i na predavanjima..
Gelfandova se vise ne cini tak strasna, ali onaj primjer sa l^1(Z) je malo previse.. ne bih se nikad sjetio da iskoristim da je dual l^besk (iako se sjecam s kolokvija)
uglavnom, laku noc..
_________________  |
|
| [Vrh] |
|
Ilja
Forumaš(ica)
Pridružen/a: 30. 10. 2002. (22:22:31)
Postovi: (1AF)16
|
| Postano: 13:29 čet, 10. 5. 2007 Naslov: |
|
|
|
[quote="MB"]evo glupavih pitanja nakon previse ucenja:
1. jel bitan clanak 'non-normal derivation...'?
2. jel se derivacija definira na komutativnoj algebri (pitam zbog Leibnitza)?
3. zasto stavljamo 'ogranicena' derivacija? jedino sto nam u tim zadacima treba je da je spektar ogranicen, a to imamo bez obzira kakav je operator, zar ne? ako se misli da je derivacija ogranicena kao lin. op., kud onda spada ona prica s kompaktnih op. kad smo pokazivali da u C([0,1]) derivacija nije neprekidna?
4. kak znamo da je bijekcija CH prostora homeomorfizam? pojavljuje se u nekom zadatku i na predavanjima..
Gelfandova se vise ne cini tak strasna, ali onaj primjer sa l^1(Z) je malo previse.. ne bih se nikad sjetio da iskoristim da je dual l^besk (iako se sjecam s kolokvija)
uglavnom, laku noc..[/quote]
1. ovisi što smatraš bitnim. Za kolokvij nije.
2. Da. Npr. ovdje imaš jedan članak vezan uz derivacije na komutativnim algebrama:
http://links.jstor.org/sici?sici=0002-9939%28198201%2984%3A1%3C60%3ADOCBA%3E2.0.CO%3B2-6&size=LARGE&origin=JSTOR-enlargePage
3. Na kompaktnim operatorima pokazali da na prostoru funkcija klase [latex]C^\infty([0,1])[/latex] ne postoji norma obzirom na koju je (standardna) derivacija neprekdina. No postoje derivacije koje su neprekdina. Ono što se zna da je na nivou C*-algebri svaka derivacija nužno neprekidna. Derivacije se između ostalog proučavaju radi dobivanja invarijanti Banachovih algebri. Kao u algebarskoj topologiji, i ovdje konstruiraš niz grupa (tzv. Hochschildova kohomologija) koje imaju veze sa ponašanjem derivacija na toj algebri. No to sad nije bitno.
4. Zato što je inverz neprekidne bijekcije sa kompakta na neki skup (koji također mora biti kompaktan jer je neprekidna slika kompakta) automatski neprekidan, tj. homeomorfizam. Mislim je da to dokazano u analizi 3.
Zadatak sa Gelfandovom transformacijom algebri [latex]\ell^{1}(\mathbb{Z}_n)[/latex] i [latex]\ell^{1}(\mathbb{Z})[/latex] služe samo kao motivacijski primjer da Gelfandova transformacija na grupovnim algebrama (imaš u vježbama što je to) korespondira Fourierovoj transformaciji. O tome sam bio pričao prošli put na vježbama.
| MB (napisa): | evo glupavih pitanja nakon previse ucenja:
1. jel bitan clanak 'non-normal derivation...'?
2. jel se derivacija definira na komutativnoj algebri (pitam zbog Leibnitza)?
3. zasto stavljamo 'ogranicena' derivacija? jedino sto nam u tim zadacima treba je da je spektar ogranicen, a to imamo bez obzira kakav je operator, zar ne? ako se misli da je derivacija ogranicena kao lin. op., kud onda spada ona prica s kompaktnih op. kad smo pokazivali da u C([0,1]) derivacija nije neprekidna?
4. kak znamo da je bijekcija CH prostora homeomorfizam? pojavljuje se u nekom zadatku i na predavanjima..
Gelfandova se vise ne cini tak strasna, ali onaj primjer sa l^1(Z) je malo previse.. ne bih se nikad sjetio da iskoristim da je dual l^besk (iako se sjecam s kolokvija)
uglavnom, laku noc.. |
1. ovisi što smatraš bitnim. Za kolokvij nije.
2. Da. Npr. ovdje imaš jedan članak vezan uz derivacije na komutativnim algebrama:
http://links.jstor.org/sici?sici=0002-9939%28198201%2984%3A1%3C60%3ADOCBA%3E2.0.CO%3B2-6&size=LARGE&origin=JSTOR-enlargePage
3. Na kompaktnim operatorima pokazali da na prostoru funkcija klase 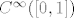 ne postoji norma obzirom na koju je (standardna) derivacija neprekdina. No postoje derivacije koje su neprekdina. Ono što se zna da je na nivou C*-algebri svaka derivacija nužno neprekidna. Derivacije se između ostalog proučavaju radi dobivanja invarijanti Banachovih algebri. Kao u algebarskoj topologiji, i ovdje konstruiraš niz grupa (tzv. Hochschildova kohomologija) koje imaju veze sa ponašanjem derivacija na toj algebri. No to sad nije bitno.
4. Zato što je inverz neprekidne bijekcije sa kompakta na neki skup (koji također mora biti kompaktan jer je neprekidna slika kompakta) automatski neprekidan, tj. homeomorfizam. Mislim je da to dokazano u analizi 3.
Zadatak sa Gelfandovom transformacijom algebr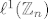i  i 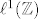 služe samo kao motivacijski primjer da Gelfandova transformacija na grupovnim algebrama (imaš u vježbama što je to) korespondira Fourierovoj transformaciji. O tome sam bio pričao prošli put na vježbama.
|
|
| [Vrh] |
|
MB
Forumaš(ica)
Pridružen/a: 01. 07. 2005. (12:35:21)
Postovi: (224)16
Spol:
Lokacija: Molvice
|
|
| [Vrh] |
|
Ilja
Forumaš(ica)
Pridružen/a: 30. 10. 2002. (22:22:31)
Postovi: (1AF)16
|
| Postano: 16:09 sri, 16. 5. 2007 Naslov: |
|
|
|
U attachmentu je kolokvij s rješenjima. Ako uočite neki tipfeler, javite.
U attachmentu je kolokvij s rješenjima. Ako uočite neki tipfeler, javite.
| Description: |
|
Download |
| Filename: |
Czvijezda-kol1-0607.pdf |
| Filesize: |
112.45 KB |
| Downloaded: |
379 Time(s) |
|
|
| [Vrh] |
|
MB
Forumaš(ica)
Pridružen/a: 01. 07. 2005. (12:35:21)
Postovi: (224)16
Spol:
Lokacija: Molvice
|
|
| [Vrh] |
|
Ilja
Forumaš(ica)
Pridružen/a: 30. 10. 2002. (22:22:31)
Postovi: (1AF)16
|
|
| [Vrh] |
|
|
)