| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
dancy
Forumaš(ica)

Pridružen/a: 22. 09. 2007. (22:02:57)
Postovi: (D)16
|
|
| [Vrh] |
|
vsego
Site Admin


Pridružen/a: 06. 10. 2002. (22:07:09)
Postovi: (3562)16
Spol: 
Lokacija: /sbin/init
|
 Postano: 19:26 ned, 23. 9. 2007 Naslov: Postano: 19:26 ned, 23. 9. 2007 Naslov: |
    |
|
|
Cek... a zasto, na primjer, [latex]x^2+2x+1 = 0[/latex] ne bi imala realno rjesenje? :shock:
Diskriminanata je [latex]b^2-4ac = k_1^2-4k_2[/latex] i tebi treba da je to vece ili jednako nuli. :) Dakle: [latex]k_1^2 \geq 4k_2[/latex] 8)
I sada provjeris kad je to istina (ako nikako drugacije, imas 36 kandidata ili 6 linearnih nejednadzbi). 8) Ako nisam fulao, takvih ima 19 od 36, sto je 0.527778. :D
Ovo sto si ti rijesila lici mi na "bacamo [b]jednu[/b] kocku, rezultat je [i]k[/i], kolika je vjerojatnost da jednadzba [latex]x^2 + kx + k = 0[/latex] ima realna rjesenja?" :?
Cek... a zasto, na primjer, 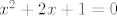 ne bi imala realno rjesenje? ne bi imala realno rjesenje? 
Diskriminanata je 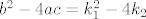 i tebi treba da je to vece ili jednako nuli. i tebi treba da je to vece ili jednako nuli.  Dakle: Dakle: 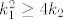 
I sada provjeris kad je to istina (ako nikako drugacije, imas 36 kandidata ili 6 linearnih nejednadzbi).  Ako nisam fulao, takvih ima 19 od 36, sto je 0.527778. Ako nisam fulao, takvih ima 19 od 36, sto je 0.527778. 
Ovo sto si ti rijesila lici mi na "bacamo jednu kocku, rezultat je k, kolika je vjerojatnost da jednadzba 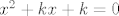 ima realna rjesenja?" ima realna rjesenja?" 
_________________ U pravilu ignoriram pitanja u krivim topicima i kodove koji nisu u [code]...[/code] blokovima.
Takodjer, OBJASNITE sto vas muci! "Sto mi je krivo?", bez opisa u cemu je problem, rijetko ce zadobiti moju paznju.  |
|
| [Vrh] |
|
goranm
Forumaš(ica)


Pridružen/a: 12. 11. 2002. (20:09:12)
Postovi: (906)16
Spol: 
|
 Postano: 20:37 ned, 23. 9. 2007 Naslov: Re: rok 3.9.2007. Postano: 20:37 ned, 23. 9. 2007 Naslov: Re: rok 3.9.2007. |
    |
|
|
[quote="dancy"]Dakle, jednadzba ima realna rjesenja ako je diskriminanta >=0.
Buduci da sl.varijable K1 i K2 primaju iste vrijednosti, zanima me da li ih mogu gledat kao isto... pa bi gornju jednadzbu pisala kao
xna2 + K1*x + K1=0.[/quote]
Ne možeš. Slučajne varijable K1 i K2 imaju istu razdiobu, ali mogu istovremeno poprimiti različite vrijednosti.
Ako imaju isti zakon razdiobe, to znači da određenu vrijednost primaju s istom vjerojatnošću, tj. [latex]P(K_1=k)=P(K_2=k), k \in \{1,2,3,4,5,6\}[/latex], što je opet različito od [latex]K_1=K_2[/latex] ili [latex]P(K_1=K_2).[/latex]
A ako je [latex]P(K_1=K_2)=1[/latex], onda se kaže da su sl. varijable K1 i K2 [u][b]gotovo sigurno jednake[/b][/u] i mislim da tek u tom slučaju možeš primijeniti to što si primijenila. A lako se vidi da je [latex]P(K_1=K_2)\neq 1.[/latex]
Ti tražiš vjerojatnost [latex]P(K_1^2 -4K_2 \geq 0)=P(K_1^2 \geq 4K_2)[/latex]
Kako je
[latex]K_1 = \left (
\begin{array}{cccccc}
1 & 2 & 3 & 4 & 5 & 6 \\
\frac{1}{6}&\frac{1}{6}&\frac{1}{6}&\frac{1}{6}&\frac{1}{6}&\frac{1}{6}
\end{array}
\right)
[/latex]
onda je
[latex]K_1^2 = \left (
\begin{array}{cccccc}
1 & 4 & 9 & 16 & 25 & 36 \\
\frac{1}{6}&\frac{1}{6}&\frac{1}{6}&\frac{1}{6}&\frac{1}{6}&\frac{1}{6}
\end{array}
\right)
[/latex],
a isto tako je
[latex]4K_2 = \left (
\begin{array}{cccccc}
4 & 8 & 12 & 16 & 20 & 24 \\
\frac{1}{6}&\frac{1}{6}&\frac{1}{6}&\frac{1}{6}&\frac{1}{6}&\frac{1}{6}
\end{array}
\right)
[/latex].
Možeš pretpostaviti da su K1 i K2 nezavisne sl. varijable pa je onda
[latex]P(K_1^2 \geq 4K_2)=P(K^2_1=4,4K_2=4)+\\
+P(K^2_1=9)(P(4K_2=4)+P(4K_2=8))+\dots=\frac{19}{36}[/latex]
| dancy (napisa): | Dakle, jednadzba ima realna rjesenja ako je diskriminanta >=0.
Buduci da sl.varijable K1 i K2 primaju iste vrijednosti, zanima me da li ih mogu gledat kao isto... pa bi gornju jednadzbu pisala kao
xna2 + K1*x + K1=0. |
Ne možeš. Slučajne varijable K1 i K2 imaju istu razdiobu, ali mogu istovremeno poprimiti različite vrijednosti.
Ako imaju isti zakon razdiobe, to znači da određenu vrijednost primaju s istom vjerojatnošću, tj. 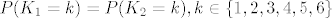 , što je opet različito od , što je opet različito od 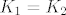 ili ili 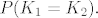
A ako je 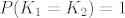 , onda se kaže da su sl. varijable K1 i K2 gotovo sigurno jednake i mislim da tek u tom slučaju možeš primijeniti to što si primijenila. A lako se vidi da je , onda se kaže da su sl. varijable K1 i K2 gotovo sigurno jednake i mislim da tek u tom slučaju možeš primijeniti to što si primijenila. A lako se vidi da je 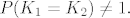
Ti tražiš vjerojatnost 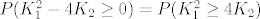
Kako je
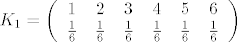
onda je
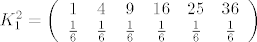 , ,
a isto tako je
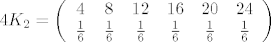 . .
Možeš pretpostaviti da su K1 i K2 nezavisne sl. varijable pa je onda
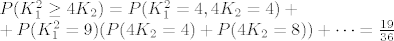
_________________
The Dude Abides
Zadnja promjena: goranm; 23:27 sub, 13. 9. 2008; ukupno mijenjano 2 put/a.
|
|
| [Vrh] |
|
dancy
Forumaš(ica)

Pridružen/a: 22. 09. 2007. (22:02:57)
Postovi: (D)16
|
|
| [Vrh] |
|
|






