| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
blob
Forumaš(ica)


Pridružen/a: 13. 07. 2007. (18:09:52)
Postovi: (23)16
|
 Postano: 18:48 uto, 15. 4. 2008 Naslov: Zadatak s današnjeg blica Postano: 18:48 uto, 15. 4. 2008 Naslov: Zadatak s današnjeg blica |
    |
|
|
U prvom zadatku je jedna grupa dobila linearni operator [latex]f:\mathbb{R}^3 \rightarrow \mathbb{R}^3[/latex], našla njegov matrični prikaz (3x3 matrica) i dobila dvije svojstvene vrijednosti: jednu algebarske kratnosti 1, i jednu algebarske kratnosti 2. Bilo je pitanje može li se nešto reći o dijagonalizabilnosti ovog operatora, BEZ da se računaju svojstveni vektori i geometrijske kratnosti svojstvenih vrijednosti.
E sad, imamo teorem da je [latex]f:V\rightarrow V[/latex] dijagonalizabilan ako i samo ako se za svaku svojstvenu vrijednost [latex]\lambda[/latex] od [latex]f[/latex] njena geometrijska poklapa sa algebarskom kratnošću. Isto tako znamo da za svojstvenu vrijednost [latex]\lambda[/latex] vrijedi [latex]1 \leq g_{\lambda} \leq a_{\lambda}[/latex], gdje je [latex]g_{\lambda}[/latex] geometrijska, a [latex]a_{\lambda}[/latex] algebarska kratnost od [latex]\lambda[/latex].
Ako znamo da je za neku [latex]\lambda[/latex] njena algebarska kratnost 2, vidimo da njena geometrijska kratnost može biti ili 1 ili 2, a to pak ne možemo točno odrediti bez računanja svojstvenih vektora, promatranja dimenzije svojstvenog potprostora za tu [latex]\lambda[/latex], odnosno njene geometrijske kratnosti.
Dakle, odgovor bi bio da, poznavajući samo algebarsku kratnost svojstvene vrijednosti [latex]\lambda[/latex] koja je jednaka 2, ne možemo odrediti je li [latex]f[/latex] dijagonalizabilan.
Je li tako?
[size=9](Naravno, kada bi dobili 3 različite [latex]\lambda[/latex], svaka algebarske kratnosti 1, onda bi iz gornjih tvrdnji slijedilo i da su njihove geometrijske kratnosti jednake 1 i da je u tom slučaju operator dijagonalizabilan.)[/size]
U prvom zadatku je jedna grupa dobila linearni operator 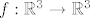 , našla njegov matrični prikaz (3x3 matrica) i dobila dvije svojstvene vrijednosti: jednu algebarske kratnosti 1, i jednu algebarske kratnosti 2. Bilo je pitanje može li se nešto reći o dijagonalizabilnosti ovog operatora, BEZ da se računaju svojstveni vektori i geometrijske kratnosti svojstvenih vrijednosti. , našla njegov matrični prikaz (3x3 matrica) i dobila dvije svojstvene vrijednosti: jednu algebarske kratnosti 1, i jednu algebarske kratnosti 2. Bilo je pitanje može li se nešto reći o dijagonalizabilnosti ovog operatora, BEZ da se računaju svojstveni vektori i geometrijske kratnosti svojstvenih vrijednosti.
E sad, imamo teorem da je 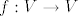 dijagonalizabilan ako i samo ako se za svaku svojstvenu vrijednost dijagonalizabilan ako i samo ako se za svaku svojstvenu vrijednost  od od  njena geometrijska poklapa sa algebarskom kratnošću. Isto tako znamo da za svojstvenu vrijednost njena geometrijska poklapa sa algebarskom kratnošću. Isto tako znamo da za svojstvenu vrijednost  vrijedi vrijedi 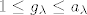 , gdje je , gdje je 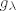 geometrijska, a geometrijska, a 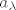 algebarska kratnost od algebarska kratnost od  . .
Ako znamo da je za neku  njena algebarska kratnost 2, vidimo da njena geometrijska kratnost može biti ili 1 ili 2, a to pak ne možemo točno odrediti bez računanja svojstvenih vektora, promatranja dimenzije svojstvenog potprostora za tu njena algebarska kratnost 2, vidimo da njena geometrijska kratnost može biti ili 1 ili 2, a to pak ne možemo točno odrediti bez računanja svojstvenih vektora, promatranja dimenzije svojstvenog potprostora za tu  , odnosno njene geometrijske kratnosti. , odnosno njene geometrijske kratnosti.
Dakle, odgovor bi bio da, poznavajući samo algebarsku kratnost svojstvene vrijednosti  koja je jednaka 2, ne možemo odrediti je li koja je jednaka 2, ne možemo odrediti je li  dijagonalizabilan. dijagonalizabilan.
Je li tako?
(Naravno, kada bi dobili 3 različite  , svaka algebarske kratnosti 1, onda bi iz gornjih tvrdnji slijedilo i da su njihove geometrijske kratnosti jednake 1 i da je u tom slučaju operator dijagonalizabilan.) , svaka algebarske kratnosti 1, onda bi iz gornjih tvrdnji slijedilo i da su njihove geometrijske kratnosti jednake 1 i da je u tom slučaju operator dijagonalizabilan.)
|
|
| [Vrh] |
|
Gost
|
 Postano: 19:44 uto, 15. 4. 2008 Naslov: Postano: 19:44 uto, 15. 4. 2008 Naslov: |
    |
|
|
Valjda... Tako sam i ja dobila.
Samo sto sam ja raspisala dalje. .
Gledajuci algebarsku kratnost, zakljucujem da geometrijska moze biti ili 1 ili 2, pa sam raspisala slucajeve:
1. ako je geom. kratnost 1, f se moze dijagonalizirati,
dok se u suprotnom (tj. ako je geom. kratnost 2) ne moze.
No, koji slucaj zaista vrijedi, ne moze se odrediti bez odredivanja svojstvenih vektora.
Valjda... Tako sam i ja dobila.
Samo sto sam ja raspisala dalje. .
Gledajuci algebarsku kratnost, zakljucujem da geometrijska moze biti ili 1 ili 2, pa sam raspisala slucajeve:
1. ako je geom. kratnost 1, f se moze dijagonalizirati,
dok se u suprotnom (tj. ako je geom. kratnost 2) ne moze.
No, koji slucaj zaista vrijedi, ne moze se odrediti bez odredivanja svojstvenih vektora.
|
|
| [Vrh] |
|
Masiela
Forumaš(ica)


Pridružen/a: 11. 09. 2007. (22:28:01)
Postovi: (338)16
Spol: 
Lokacija: Među bananama
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
Masiela
Forumaš(ica)


Pridružen/a: 11. 09. 2007. (22:28:01)
Postovi: (338)16
Spol: 
Lokacija: Među bananama
|
|
| [Vrh] |
|
Ally
Forumaš(ica)

Pridružen/a: 15. 04. 2008. (19:57:23)
Postovi: (7F)16
Spol: 
|
|
| [Vrh] |
|
Masiela
Forumaš(ica)


Pridružen/a: 11. 09. 2007. (22:28:01)
Postovi: (338)16
Spol: 
Lokacija: Među bananama
|
|
| [Vrh] |
|
|








