| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
Liddy
Forumaš(ica)


Pridružen/a: 17. 08. 2004. (10:03:41)
Postovi: (169)16
|
|
| [Vrh] |
|
Anja
Forumaš(ica)


Pridružen/a: 24. 03. 2003. (10:51:07)
Postovi: (132)16
|
|
| [Vrh] |
|
loreal
Forumaš(ica)


Pridružen/a: 09. 02. 2008. (18:30:35)
Postovi: (33)16
Spol: 
Lokacija: sava
|
|
| [Vrh] |
|
Pukica
Forumaš(ica)


Pridružen/a: 22. 10. 2004. (16:42:51)
Postovi: (1A5)16
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
alen
Forumaš(ica)


Pridružen/a: 14. 10. 2005. (23:25:58)
Postovi: (221)16
|
 Postano: 12:28 uto, 22. 4. 2008 Naslov: Postano: 12:28 uto, 22. 4. 2008 Naslov: |
    |
|
|
Evo rješenja
Evo rješenja
_________________
Između ostalog, mislim da bi kolegij mjera i integral trebao imati svoj podforum među kolegijima treće godine
| Description: |
|

Download |
| Filename: |
ispravak 5a.pdf |
| Filesize: |
30.79 KB |
| Downloaded: |
438 Time(s) |
| Description: |
|

Download |
| Filename: |
ispravak 3a.pdf |
| Filesize: |
25.45 KB |
| Downloaded: |
354 Time(s) |
| Description: |
|

Download |
| Filename: |
ispravak 7b.pdf |
| Filesize: |
20.77 KB |
| Downloaded: |
358 Time(s) |
| Description: |
|

Download |
| Filename: |
ka zad.pdf |
| Filesize: |
844.99 KB |
| Downloaded: |
536 Time(s) |
Zadnja promjena: alen; 17:32 uto, 22. 4. 2008; ukupno mijenjano 3 put/a.
|
|
| [Vrh] |
|
Pukica
Forumaš(ica)


Pridružen/a: 22. 10. 2004. (16:42:51)
Postovi: (1A5)16
|
|
| [Vrh] |
|
Anja
Forumaš(ica)


Pridružen/a: 24. 03. 2003. (10:51:07)
Postovi: (132)16
|
|
| [Vrh] |
|
loreal
Forumaš(ica)


Pridružen/a: 09. 02. 2008. (18:30:35)
Postovi: (33)16
Spol: 
Lokacija: sava
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
jakov
Forumaš(ica)

Pridružen/a: 30. 08. 2006. (20:03:41)
Postovi: (47)16
Spol: 
Lokacija: evo me doma
|
 Postano: 18:35 pet, 13. 6. 2008 Naslov: Postano: 18:35 pet, 13. 6. 2008 Naslov: |
    |
|
|
Evo onih lakših:
3. a) z[size=9][/size]k[size=12][/size]=ln2 + i(2k + 1)pi, k e Z ->pol reda 1; beskonačno je bitan singularitet.
b) 0 je pol reda 2, a beskonačno je bitan singularitet.
c) 0 je bitan singularitet, beskonačno nije singularitet.
d) 0 je uklonjiv singularitet, beskonačno je bitan singularitet.
4. ipi(e-2)/2.
6. pi/2.
7. 2pi/3.
Nadam se da pomaže.
Evo onih lakših:
3. a) zk=ln2 + i(2k + 1)pi, k e Z →pol reda 1; beskonačno je bitan singularitet.
b) 0 je pol reda 2, a beskonačno je bitan singularitet.
c) 0 je bitan singularitet, beskonačno nije singularitet.
d) 0 je uklonjiv singularitet, beskonačno je bitan singularitet.
4. ipi(e-2)/2.
6. pi/2.
7. 2pi/3.
Nadam se da pomaže.
_________________
"Čovjek radi cijeli život da bi bio poznat, a onda ide po svijetu s tamnim naočalama da ga ne bi prepoznali." W. S. Maugham
Zadnja promjena: jakov; 13:13 pon, 16. 6. 2008; ukupno mijenjano 1 put.
|
|
| [Vrh] |
|
Anja
Forumaš(ica)


Pridružen/a: 24. 03. 2003. (10:51:07)
Postovi: (132)16
|
|
| [Vrh] |
|
alen
Forumaš(ica)


Pridružen/a: 14. 10. 2005. (23:25:58)
Postovi: (221)16
|
|
| [Vrh] |
|
MB
Forumaš(ica)


Pridružen/a: 01. 07. 2005. (12:35:21)
Postovi: (224)16
Spol: 
Lokacija: Molvice
|
 Postano: 15:56 uto, 17. 6. 2008 Naslov: Postano: 15:56 uto, 17. 6. 2008 Naslov: |
    |
|
|
pomalo sam zaboravio odredjene trikove, ali ono sto uvijek mozes napraviti ako ti se da racunati je slijedece:
tvoj res je zapravo [latex]res(\frac{e^{\frac{1}{w}}}{(w+4)^{10}+1},0)[/latex].
[latex]e^{1/w}[/latex] znas razviti u red oko 0, a za nazivnik mozes izračunati red rjesavanjem sustava kojeg dobijes iz
[latex]((w+4)^{10}+1)(a_0+a_1w+a_2w^2+...)=1[/latex] pri cemu koristis binomni poucak.
Kad to izracunas, pomnozis red od [latex]e^{1/w}[/latex] i [latex]a_0+a_1w+a_2w^2+...[/latex] i pogledas sto ti stoji uz [latex]w^{-1}[/latex].
Nadam se da racun nije prestrasan i da na kraju dobije sumu koju znas izracunati.
Nekako mi se cini da postoji laksi nacin, ali mozda se u ovom postupku krije kako izvesti neku formulu ili metodu.
pomalo sam zaboravio odredjene trikove, ali ono sto uvijek mozes napraviti ako ti se da racunati je slijedece:
tvoj res je zapravo 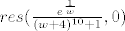 . .
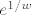 znas razviti u red oko 0, a za nazivnik mozes izračunati red rjesavanjem sustava kojeg dobijes iz znas razviti u red oko 0, a za nazivnik mozes izračunati red rjesavanjem sustava kojeg dobijes iz
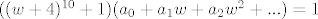 pri cemu koristis binomni poucak. pri cemu koristis binomni poucak.
Kad to izracunas, pomnozis red od 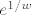 i i 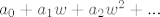 i pogledas sto ti stoji uz i pogledas sto ti stoji uz 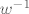 . .
Nadam se da racun nije prestrasan i da na kraju dobije sumu koju znas izracunati.
Nekako mi se cini da postoji laksi nacin, ali mozda se u ovom postupku krije kako izvesti neku formulu ili metodu.
_________________  |
|
| [Vrh] |
|
|








