| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
gulf56
Forumaš(ica)
Pridružen/a: 08. 05. 2008. (17:25:04)
Postovi: (6)16
|
 Postano: 17:33 čet, 8. 5. 2008 Naslov: Kvadratna nejednadzba Postano: 17:33 čet, 8. 5. 2008 Naslov: Kvadratna nejednadzba |
    |
|
|
Pozdrav ! Novi sam na forumu, ali moram reci da je ovo najbolji forum koji sam uspjeo pronaći na temu matematike.
Trebam malu pomoć, radi se o slijedećem zadatku:
(X+2/X+3) - (X+1/X-1) >= (4/X²+2x-3)
Zadatak je jednostavan, ali moje rješenje se ne poklapa sa rješenjem iz zbirke, da dokažem da se ne radi o rješavanju domaćih zataka, neću tražiti kompletan postupak rješavanja zadatka nego samo rješenje, odnosno x. Pripremam se za važan pismeni i tip ovakvog zadatka očekujem kao najlakši, a već sam zapeo ... inače imam jako dobre ocjene. Samo se želim uvjeriti šta je tačno ...
Pozdrav ! Novi sam na forumu, ali moram reci da je ovo najbolji forum koji sam uspjeo pronaći na temu matematike.
Trebam malu pomoć, radi se o slijedećem zadatku:
(X+2/X+3) - (X+1/X-1) >= (4/X²+2x-3)
Zadatak je jednostavan, ali moje rješenje se ne poklapa sa rješenjem iz zbirke, da dokažem da se ne radi o rješavanju domaćih zataka, neću tražiti kompletan postupak rješavanja zadatka nego samo rješenje, odnosno x. Pripremam se za važan pismeni i tip ovakvog zadatka očekujem kao najlakši, a već sam zapeo ... inače imam jako dobre ocjene. Samo se želim uvjeriti šta je tačno ...
|
|
| [Vrh] |
|
vsego
Site Admin


Pridružen/a: 06. 10. 2002. (22:07:09)
Postovi: (3562)16
Spol: 
Lokacija: /sbin/init
|
 Postano: 17:52 čet, 8. 5. 2008 Naslov: Postano: 17:52 čet, 8. 5. 2008 Naslov: |
    |
|
|
Mala preporuka: slaz zagrade kako treba. :) Pretpostavljam da je prvi clan
[latex]\frac{x+2}{x+3}[/latex],
a ne (kako tvoje zagrade aludiraju)
[latex]x+\frac{2}{x}+3[/latex]. :)
Svedi desnu stranu na zajednicki nazivnik:
[latex]\frac{(x+2)(x-1) - (x+3)(x+1)}{(x+3)(x-1)} \geq \frac4{x^2+2x-3}[/latex]
[latex]-\frac{3x+5}{(x+3)(x-1)} \geq \frac4{(x+3)(x-1)}[/latex]
Mnozimo s nazivnikom. :)
Za [latex]x \in \langle -3, 1 \rangle[/latex] je nazivnik negativan, pa se okrece nejednakost; inace ne. :)
1. Slucaj [latex]x \in \langle -3, 1 \rangle[/latex]:
[latex]-3x-5 \leq 4[/latex]
[latex]x \geq -3[/latex]
Dakle: [latex]x \in \langle -3, 1 \rangle[/latex].
2. Slucaj [latex]x \not\in \langle -3, 1 \rangle[/latex]:
[latex]-3x-5 \geq 4[/latex]
[latex]x \leq -3[/latex]
Dakle: [latex]x \in \langle -\infty, -3 \rangle[/latex].
Ukupno: [latex]x \in \langle -\infty, 1 \rangle \setminus \{-3\}[/latex]. 8)
Disklejmer: zurim na hranidbu, pa nisam provjeravao i greske su moguce (dapace, vjerojatne). ;)
Mala preporuka: slaz zagrade kako treba.  Pretpostavljam da je prvi clan Pretpostavljam da je prvi clan
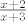 , ,
a ne (kako tvoje zagrade aludiraju)
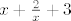 . . 
Svedi desnu stranu na zajednicki nazivnik:
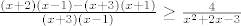
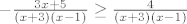
Mnozimo s nazivnikom. 
Za 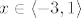 je nazivnik negativan, pa se okrece nejednakost; inace ne. je nazivnik negativan, pa se okrece nejednakost; inace ne. 
1. Slucaj 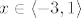 : :
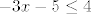

Dakle: 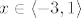 . .
2. Slucaj 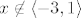 : :
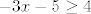
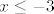
Dakle: 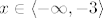 . .
Ukupno: 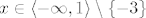 . . 
Disklejmer: zurim na hranidbu, pa nisam provjeravao i greske su moguce (dapace, vjerojatne). 
_________________ U pravilu ignoriram pitanja u krivim topicima i kodove koji nisu u [code]...[/code] blokovima.
Takodjer, OBJASNITE sto vas muci! "Sto mi je krivo?", bez opisa u cemu je problem, rijetko ce zadobiti moju paznju.  |
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
gulf56
Forumaš(ica)
Pridružen/a: 08. 05. 2008. (17:25:04)
Postovi: (6)16
|
|
| [Vrh] |
|
Luuka
Forumaš(ica)


Pridružen/a: 13. 02. 2007. (20:34:54)
Postovi: (925)16
Spol: 
Lokacija: Hakuna Matata
|
 Postano: 18:07 čet, 8. 5. 2008 Naslov: Postano: 18:07 čet, 8. 5. 2008 Naslov: |
    |
|
|
[quote="vsego"]
Mnozimo s nazivnikom. :)
[/quote]
Pa zar nije "bolje" (kako su mene učili u srednoj ;), ne trebaš pazit na znak nejednakosti, sve lagana šablona) sve prebacit na jednu stranu,dobije se "neki razlomak veći/manji od nule" , faktorizirat (u ovom slučaju to je odmah gotovo) pa onda nacrtat onu tablicu u kojoj se upišu svi faktori, sve nultočke pa se promatraju predznaci. I na kraju se svi predznaci po stupcu izmnože i gleda se minus ili plus ovisno dal imamo veće ili manje od nule. (i ofkors paze se na zagrade, ovisno jel faktor u brojniku ili nazivniku ako imamo >= ili <= od nule) :D
8)
...ako je itko skužio o čemu pričam... :?
btw za ovaj zadatak je jednostavnije kak je vsego, ali mislim da je kod kompliciranih izraza jednostavnije preko tablice ;)
| vsego (napisa): |
Mnozimo s nazivnikom. 
|
Pa zar nije "bolje" (kako su mene učili u srednoj  , ne trebaš pazit na znak nejednakosti, sve lagana šablona) sve prebacit na jednu stranu,dobije se "neki razlomak veći/manji od nule" , faktorizirat (u ovom slučaju to je odmah gotovo) pa onda nacrtat onu tablicu u kojoj se upišu svi faktori, sve nultočke pa se promatraju predznaci. I na kraju se svi predznaci po stupcu izmnože i gleda se minus ili plus ovisno dal imamo veće ili manje od nule. (i ofkors paze se na zagrade, ovisno jel faktor u brojniku ili nazivniku ako imamo >= ili ⇐ od nule) , ne trebaš pazit na znak nejednakosti, sve lagana šablona) sve prebacit na jednu stranu,dobije se "neki razlomak veći/manji od nule" , faktorizirat (u ovom slučaju to je odmah gotovo) pa onda nacrtat onu tablicu u kojoj se upišu svi faktori, sve nultočke pa se promatraju predznaci. I na kraju se svi predznaci po stupcu izmnože i gleda se minus ili plus ovisno dal imamo veće ili manje od nule. (i ofkors paze se na zagrade, ovisno jel faktor u brojniku ili nazivniku ako imamo >= ili ⇐ od nule) 

...ako je itko skužio o čemu pričam... 
btw za ovaj zadatak je jednostavnije kak je vsego, ali mislim da je kod kompliciranih izraza jednostavnije preko tablice 
_________________ "Bolje bi prolazio na faxu da sam na drogama nego na netu" - by a friend of mine
"Poslije spavanja doma spavanje bilo di mi je najdraža stvar" - by the same guy  |
|
| [Vrh] |
|
ma
Forumaš(ica)


Pridružen/a: 27. 01. 2007. (12:06:50)
Postovi: (347)16
Spol: 
|
 Postano: 22:55 čet, 8. 5. 2008 Naslov: Postano: 22:55 čet, 8. 5. 2008 Naslov: |
    |
|
|
[quote="Luuka"]...ako je itko skužio o čemu pričam... :?[/quote]
:lol: da, ja znam o čemu pričaš. samo, ne znam možemo li reći što je 'bolje' kad su oba načina točna. kako kome paše :)
meni je isto tablica draža, ali samo zato što ne volim množiti s nečim za što uopće ne znam što je :shock: - ja sad tu množim s nekim x-om, a ne znam jel on manji, veći ili jednak 0.
| Luuka (napisa): | ...ako je itko skužio o čemu pričam...  |
 da, ja znam o čemu pričaš. samo, ne znam možemo li reći što je 'bolje' kad su oba načina točna. kako kome paše da, ja znam o čemu pričaš. samo, ne znam možemo li reći što je 'bolje' kad su oba načina točna. kako kome paše 
meni je isto tablica draža, ali samo zato što ne volim množiti s nečim za što uopće ne znam što je  - ja sad tu množim s nekim x-om, a ne znam jel on manji, veći ili jednak 0. - ja sad tu množim s nekim x-om, a ne znam jel on manji, veći ili jednak 0.
_________________
ima let u finish
|
|
| [Vrh] |
|
Luuka
Forumaš(ica)


Pridružen/a: 13. 02. 2007. (20:34:54)
Postovi: (925)16
Spol: 
Lokacija: Hakuna Matata
|
|
| [Vrh] |
|
vsego
Site Admin


Pridružen/a: 06. 10. 2002. (22:07:09)
Postovi: (3562)16
Spol: 
Lokacija: /sbin/init
|
|
| [Vrh] |
|
Markec
Forumaš(ica)

Pridružen/a: 20. 02. 2003. (14:49:45)
Postovi: (134)16
Spol: 
|
|
| [Vrh] |
|
|









