| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
Tomy007
Forumaš(ica)

Pridružen/a: 08. 11. 2009. (19:45:28)
Postovi: (94)16
|
|
| [Vrh] |
|
goranm
Forumaš(ica)


Pridružen/a: 12. 11. 2002. (20:09:12)
Postovi: (906)16
Spol: 
|
|
| [Vrh] |
|
kaj
Forumaš(ica)

Pridružen/a: 15. 11. 2009. (21:02:20)
Postovi: (B8)16
|
|
| [Vrh] |
|
mornik
Forumaš(ica)

Pridružen/a: 26. 09. 2009. (06:25:44)
Postovi: (128)16
|
 Postano: 8:52 pon, 30. 11. 2009 Naslov: Postano: 8:52 pon, 30. 11. 2009 Naslov: |
    |
|
|
Dakle, prvo želimo iskoristiti formulu za razvoj razlike kvadrata, pa ćemo pomnožiti taj izraz s [latex]\displaystyle \frac{\sqrt{n^2+n}+\sqrt[3]{n^3+n^2}}{\sqrt{n^2+n}+\sqrt[3]{n^3+n^2}}=1[/latex]. Dobivamo da sad tražimo [latex]\displaystyle \lim_{n\rightarrow +\infty} \frac{n^2+n-\sqrt[3]{(n^3+n^2)^2}}{\sqrt{n^2+n}+\sqrt[3]{n^3+n^2}}[/latex]. Podijelimo i brojnik i nazivnik s [latex]n[/latex] i dobivamo da je to jednako [latex]\displaystyle \lim_{n\rightarrow +\infty} \frac{n+1-\sqrt[3]{n^3+2n^2+n}}{\sqrt{1+\frac{1}{n}}+\sqrt[3]{1+\frac{1}{n}}}[/latex].
Sad ćemo pronaći [latex]\displaystyle \lim_{n\rightarrow +\infty}{n-\sqrt[3]{n^3+2n^2+n}}[/latex]. No, ovo nije teško - ovaj put koristimo razvoj razlike trećih potencija, pa dobivamo da je to jednako [latex]\displaystyle \lim_{n\rightarrow +\infty}{\frac{n^3-(n^3+2n^2+n)}{n^2+n\sqrt[3]{n^3+2n^2+n}+\sqrt[3]{(n^3+2n^2+n)^2}}[/latex]. Dijelimo sad i brojnik i nazivnik s [latex]n^2[/latex] i dobivamo da tražimo [latex]\displaystyle \lim_{n\rightarrow +\infty}{\frac{-2-\frac{1}{n}}{1+\sqrt[3]{1+\frac{2}{n}+\frac{1}{n^2}}+\sqrt[3]{(1+\frac{2}{n}+\frac{1}{n^2})^2}}}[/latex], a to je očito [latex]\displaystyle -\frac{2}{3}[/latex].
Sada uvrštavanjem dobivamo da limes kojeg smo tražili iznosi [latex]\displaystyle\frac{-\frac{2}{3}+1}{1+1}=\frac{1}{6}[/latex].
Vjerojatno nije baš najjednostavniji način... :) Možda bi išlo "odjednom", dakle, bez traženja pomoćnog limesa, kad bismo na početku gledali raspis razlike šestih potencija, ali to isto ne bi bilo najljepše, makar bi bilo nešto kraće.
Dakle, prvo želimo iskoristiti formulu za razvoj razlike kvadrata, pa ćemo pomnožiti taj izraz s 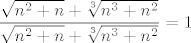 . Dobivamo da sad tražimo . Dobivamo da sad tražimo 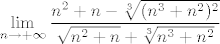 . Podijelimo i brojnik i nazivnik s . Podijelimo i brojnik i nazivnik s  i dobivamo da je to jednako i dobivamo da je to jednako 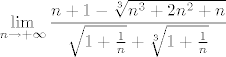 . .
Sad ćemo pronaći 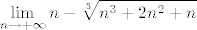 . No, ovo nije teško - ovaj put koristimo razvoj razlike trećih potencija, pa dobivamo da je to jednako . No, ovo nije teško - ovaj put koristimo razvoj razlike trećih potencija, pa dobivamo da je to jednako 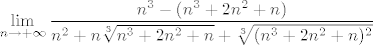 . Dijelimo sad i brojnik i nazivnik s . Dijelimo sad i brojnik i nazivnik s 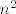 i dobivamo da tražimo i dobivamo da tražimo 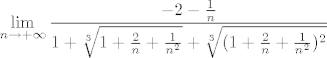 , a to je očito , a to je očito 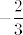 . .
Sada uvrštavanjem dobivamo da limes kojeg smo tražili iznosi 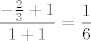 . .
Vjerojatno nije baš najjednostavniji način...  Možda bi išlo "odjednom", dakle, bez traženja pomoćnog limesa, kad bismo na početku gledali raspis razlike šestih potencija, ali to isto ne bi bilo najljepše, makar bi bilo nešto kraće. Možda bi išlo "odjednom", dakle, bez traženja pomoćnog limesa, kad bismo na početku gledali raspis razlike šestih potencija, ali to isto ne bi bilo najljepše, makar bi bilo nešto kraće.
|
|
| [Vrh] |
|
kaj
Forumaš(ica)

Pridružen/a: 15. 11. 2009. (21:02:20)
Postovi: (B8)16
|
|
| [Vrh] |
|
mornik
Forumaš(ica)

Pridružen/a: 26. 09. 2009. (06:25:44)
Postovi: (128)16
|
 Postano: 10:37 pon, 30. 11. 2009 Naslov: Postano: 10:37 pon, 30. 11. 2009 Naslov: |
    |
|
|
[quote="kaj"]I da , je li u 2.41 (b) treba biti minus u brojniku??[/quote]
A zašto ne u nazivniku? :P Ili možda treba biti [latex]3n+2[/latex] u brojniku? :P Ili je to zamka? :P (Najbolje da pitaš svog asistenta ili mu pošalješ mail...)
Inače, ako sam sad dobro na brzinu provjerio, zbilja možemo lakše na način koji spomenuh - razlika šestih potencija. Dobijemo [latex]\displaystyle \lim_{n\rightarrow +\infty}\frac{(n^2+n)^3-(n^3+n^2)^2}{(\sqrt{n^2+n})^5+(\sqrt{n^2+n})^4\sqrt[3]{n^3+n^2}+\ldots+(\sqrt[3]{n^3+n^2})^5}}[/latex]. Nakon što i brojnik i nazivnik podijelimo s [latex]n^5[/latex], lako vidimo da brojnik ide u [latex]1[/latex], a nazivnik u [latex]6[/latex]. Dakle, limes je [latex]\displaystyle \frac{1}{6}[/latex].
| kaj (napisa): | | I da , je li u 2.41 (b) treba biti minus u brojniku?? |
A zašto ne u nazivniku?  Ili možda treba biti Ili možda treba biti 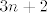 u brojniku? u brojniku?  Ili je to zamka? Ili je to zamka?  (Najbolje da pitaš svog asistenta ili mu pošalješ mail...) (Najbolje da pitaš svog asistenta ili mu pošalješ mail...)
Inače, ako sam sad dobro na brzinu provjerio, zbilja možemo lakše na način koji spomenuh - razlika šestih potencija. Dobijemo 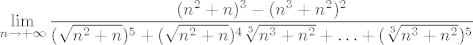 . Nakon što i brojnik i nazivnik podijelimo s . Nakon što i brojnik i nazivnik podijelimo s 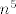 , lako vidimo da brojnik ide u , lako vidimo da brojnik ide u  , a nazivnik u , a nazivnik u  . Dakle, limes je . Dakle, limes je  . .
|
|
| [Vrh] |
|
kaj
Forumaš(ica)

Pridružen/a: 15. 11. 2009. (21:02:20)
Postovi: (B8)16
|
|
| [Vrh] |
|
pbakic
Forumaš(ica)

Pridružen/a: 05. 10. 2009. (17:48:30)
Postovi: (143)16
Spol: 
|
|
| [Vrh] |
|
NeonBlack
Forumaš(ica)

Pridružen/a: 13. 10. 2009. (15:46:24)
Postovi: (37)16
|
|
| [Vrh] |
|
kaj
Forumaš(ica)

Pridružen/a: 15. 11. 2009. (21:02:20)
Postovi: (B8)16
|
|
| [Vrh] |
|
NeonBlack
Forumaš(ica)

Pridružen/a: 13. 10. 2009. (15:46:24)
Postovi: (37)16
|
|
| [Vrh] |
|
kaj
Forumaš(ica)

Pridružen/a: 15. 11. 2009. (21:02:20)
Postovi: (B8)16
|
|
| [Vrh] |
|
Genaro
Forumaš(ica)

Pridružen/a: 27. 10. 2009. (18:57:50)
Postovi: (8B)16
Spol: 
Lokacija: Zagreb
|
 Postano: 21:53 uto, 8. 12. 2009 Naslov: Postano: 21:53 uto, 8. 12. 2009 Naslov: |
    |
|
|
Ok, dakle, zanimaju me dva zadatka:
[latex]
\\
\\2.38
\\
\\
(a)\ \ \ Izracunajte\ limese:
\\
\\
\displaystyle \lim_{n \rightarrow \infty} \Big(n - \frac{(n-a)^{3}}{(n+1)^2}\Big)
\\
\\
u\ ovisnost\ o\ parametru\ a \in \mathbb{R}[/latex]
Nisam baš siguran u način rješavanja pa me, eto, zanima.
Drugi zadatak jest:
[latex]
\\
\\
2.40
\\
(b)\ \ \ Izracunajte\ limese:
\\
\\
\\ \displaystyle \lim_{n \rightarrow \infty} \sqrt[n]{\Big(1+2^{n}+4^{n}+8^{n}+32^{n}\Big)}
[/latex]
Drugi dio bi kao trebao ispasti 32, ali kako doći do toga, nemam ideje neke.
Hvala unaprijed.
Ok, dakle, zanimaju me dva zadatka:
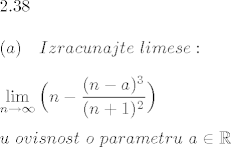
Nisam baš siguran u način rješavanja pa me, eto, zanima.
Drugi zadatak jest:
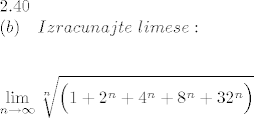
Drugi dio bi kao trebao ispasti 32, ali kako doći do toga, nemam ideje neke.
Hvala unaprijed.
|
|
| [Vrh] |
|
eve
Forumaš(ica)

Pridružen/a: 13. 07. 2009. (23:07:06)
Postovi: (192)16
Spol: 
|
|
| [Vrh] |
|
Genaro
Forumaš(ica)

Pridružen/a: 27. 10. 2009. (18:57:50)
Postovi: (8B)16
Spol: 
Lokacija: Zagreb
|
|
| [Vrh] |
|
niveus
Forumaš(ica)

Pridružen/a: 26. 10. 2009. (16:12:58)
Postovi: (5E)16
|
|
| [Vrh] |
|
mornik
Forumaš(ica)

Pridružen/a: 26. 09. 2009. (06:25:44)
Postovi: (128)16
|
 Postano: 15:15 ned, 13. 12. 2009 Naslov: Postano: 15:15 ned, 13. 12. 2009 Naslov: |
    |
|
|
Pretpostavljam da se radi o [latex]\displaystyle \lim_{n\rightarrow +\infty}\frac{1}{n^2+1}+\frac{1}{n^2+2}+\ldots+\frac{1}{n^2+n}[/latex]. Zadatak nije težak, samo se koristi usporedba s [latex]\displaystyle \frac{1}{n}[/latex] s obje strane, što je zapravo i na prvi pogled dosta prirodno budući da imamo [latex]n[/latex] pribrojnika, a svaki od njih "je sličan" [latex]\displaystyle \frac{1}{n^2}[/latex], pa je cijela suma "slična" [latex]\displaystyle n\cdot\frac{1}{n^2}=\frac{1}{n}[/latex]. Vjerojatno onda sad možeš i pretpostaviti što je limes :).
Sad kad smo stekli neku ideju kakva je otprilike ta suma, 'ajmo sad to rigorozno dokazati :):
Označimo s [latex]\displaystyle S_n:=\frac{1}{n^2+1}+\frac{1}{n^2+2}+\ldots+\frac{1}{n^2+n}[/latex]. Za svaki [latex]n\in\mathbb{N}[/latex], svaki od pribrojnika u [latex]S_n[/latex] je manji ili jednak (zapravo, strogo manji, ali nebitno) od [latex]\displaystyle \frac{1}{n^2}[/latex]. Kako pribrojnika ima točno [latex]n[/latex], vrijedi [latex]\displaystyle S_n\leq \frac{n}{n^2}=\frac{1}{n}[/latex].
Također, za svaki [latex]n\in\mathbb{N}[/latex], svaki od pribrojnika u [latex]S_n[/latex] je veći ili jednak [latex]\displaystyle \frac{1}{n^2+n}[/latex]. Ponovno, kako pribrojnika ima [latex]n[/latex], vrijedi [latex]\displaystyle S_n\geq \frac{n}{n^2+n}=\frac{1}{n+1}[/latex].
Sada imamo da za svaki [latex]n\in\mathbb{N}[/latex] vrijedi [latex]\displaystyle \frac{1}{n+1}\leq S_n\leq \frac{1}{n}[/latex]. Kako je [latex]\displaystyle \lim_{n\rightarrow +\infty}\frac{1}{n+1}=\lim_{n\rightarrow +\infty}\frac{1}{n}=0[/latex], po teoremu o sendviču je i [latex]\displaystyle \lim_{n\rightarrow +\infty} S_n=\lim_{n\rightarrow +\infty}\frac{1}{n^2+1}+\frac{1}{n^2+2}+\ldots+\frac{1}{n^2+n}=0[/latex].
Pretpostavljam da se radi o 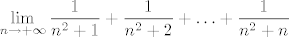 . Zadatak nije težak, samo se koristi usporedba s . Zadatak nije težak, samo se koristi usporedba s  s obje strane, što je zapravo i na prvi pogled dosta prirodno budući da imamo s obje strane, što je zapravo i na prvi pogled dosta prirodno budući da imamo  pribrojnika, a svaki od njih "je sličan" pribrojnika, a svaki od njih "je sličan" 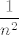 , pa je cijela suma "slična" , pa je cijela suma "slična" 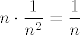 . Vjerojatno onda sad možeš i pretpostaviti što je limes . Vjerojatno onda sad možeš i pretpostaviti što je limes  . .
Sad kad smo stekli neku ideju kakva je otprilike ta suma, 'ajmo sad to rigorozno dokazati  : :
Označimo s 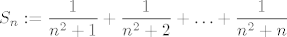 . Za svaki . Za svaki 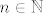 , svaki od pribrojnika u , svaki od pribrojnika u 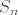 je manji ili jednak (zapravo, strogo manji, ali nebitno) od je manji ili jednak (zapravo, strogo manji, ali nebitno) od 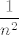 . Kako pribrojnika ima točno . Kako pribrojnika ima točno  , vrijedi , vrijedi 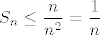 . .
Također, za svaki 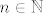 , svaki od pribrojnika u , svaki od pribrojnika u 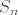 je veći ili jednak je veći ili jednak 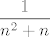 . Ponovno, kako pribrojnika ima . Ponovno, kako pribrojnika ima  , vrijedi , vrijedi 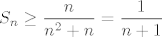 . .
Sada imamo da za svaki 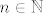 vrijedi vrijedi 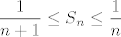 . Kako je . Kako je 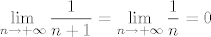 , po teoremu o sendviču je i , po teoremu o sendviču je i 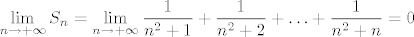 . .
|
|
| [Vrh] |
|
niveus
Forumaš(ica)

Pridružen/a: 26. 10. 2009. (16:12:58)
Postovi: (5E)16
|
|
| [Vrh] |
|
mornik
Forumaš(ica)

Pridružen/a: 26. 09. 2009. (06:25:44)
Postovi: (128)16
|
 Postano: 17:58 ned, 13. 12. 2009 Naslov: Postano: 17:58 ned, 13. 12. 2009 Naslov: |
    |
|
|
(Upozorenje: Ovo će biti dugo :lol:. Među ostalim i jer su, bar meni, takve stvari dosta zanimljive. Vjerojatno će ti trebati papir ako planiraš pomno pratiti :P.)
Nešto slično sam napisao već u prethodnom postu. Uglavnom, po mom je mišljenju u ovakvim zadacima intuicija dosta bitna stvar, bitnija od učenja čistih šablona za rješavanje zadataka. Naime, onda se pojavi ovakav zadatak kakav se tebi pojavio, koji se nije puno obrađivao na vježbama i čovjek ostane zbunjen. Tu, pod "intuicija" mislim na "kako se nešto ponaša", tj. "čemu jednostavnome to sliči". To se upravo pojavljuje u tvom zadatku - poanta je da shvatiš koliko ima pribrojnika i kako svaki od njih "izgleda".
Da dam jedan nasumični primjer (nije sa sumama, ali je ideja koju želim pokazati ista) - zanima nas [latex]\displaystyle \lim_{n\rightarrow +\infty}\frac{5\cdot 2^n+56n^4+n\sin(n)}{\sqrt[88]{2^{86+88n}+3(n\cdot \frac{2^{43+44n}}{n+\sin(n)})^2+\sqrt{\cos^2(n)+4}}}[/latex]. Jest, izraz je krajnje gnjusan (a nazivnik pomalo namješten :)). Upravo zato, pogledajmo prvo "zdravo seljački" kako se ponašaju brojnik i nazivnik, a onda ćemo odlučiti kako dalje. Nemoj da te buni ako nisi siguran/na kako bi ga riješio/la iz prve - zadatak je namjerno vrijedan prezira, zato da pokažem princip na ekstremnom primjeru kojeg je teško čak i za napisati, ali začudo neće biti toliko teško za shvatiti ideju rješenja.
Primijetit ćeš da je sve ovo što radimo upravo kako sam rekao - "zdravo seljački", što bi reklo da, makar jest u biti točno, nikako nije dovoljno rigorozno da se može prihvatiti kao legalni dokaz. Do tog dijela ćemo doći kasnije. OK, dakle, otprilike ovako razmišljamo:
Primijetimo da je [latex]5\cdot 2^n[/latex] uvjerljivo "najjači" član u brojniku: [latex]56n^4[/latex] raste puno sporije nego [latex]5\cdot 2^n[/latex], a [latex]n\sin(n)[/latex] se ponaša "negdje između" [latex]-n[/latex] i [latex]n[/latex], što je u svakom slučaju dovoljno malo da ne igra ulogu na sumu u kojoj sudjeluje [latex]2^n[/latex] (tj. [latex]5\cdot 2^n[/latex] - znamo da nam konstanta baš ni ne utječe na "red veličine" brzine rasta, da ju množi s tom konstantom). Stoga, brojnik otprilike izgleda kao [latex]5\cdot 2^n[/latex].
Pogledajmo nazivnik. Imamo [latex]88[/latex]-i korijen od svega, pa pogledajmo prvo što je ispod tog korijena. Vidimo da u sumi sudjeluje [latex]2^{86+88n}[/latex], što raste jako brzo. Sad, primijetimo da drugi pribrojnik, tj. [latex]\displaystyle 3(n\cdot \frac{2^{43+44n}}{n+\sin(n)})^2[/latex] izgleda otprilike kao [latex]3\cdot 2^{86+88n}[/latex]. To argumentiramo ovako: [latex]\displaystyle 3(n\cdot \frac{2^{43+44n}}{n+\sin(n)})^2=3\cdot 2^{86+88n}\cdot (\frac{n}{n+\sin(n)})^2[/latex]. Ovaj zadnji razlomak (pod kvadratom) ima brojnik [latex]n[/latex], a nazivnik isto "izgleda kao" [latex]n[/latex]. Naime, [latex]\sin(n)[/latex] je između [latex]-1[/latex] i [latex]1[/latex], a to "u beskonačnosti" i ne igra nekakvu ulogu kad se zbroji s [latex]n[/latex]. Dakle, [latex]\displaystyle (\frac{n}{n+\sin(n)})^2[/latex] će izgledati kao [latex]1^2=1[/latex], pa će i [latex]\displaystyle 3(n\cdot \frac{2^{43+44n}}{n+\sin(n)})^2[/latex] izgledati kao [latex]3\cdot 2^{86+88n}[/latex]. Preostaje nam još korijen od ovog izraza s kosinusom, ali to nam i nije neki problem: kako je kosinus između [latex]-1[/latex] i [latex]1[/latex], onda će i ovaj korijen biti ograničen (bit će između [latex]2=\sqrt{0+4}[/latex] i [latex]\sqrt{1^2+4}=\sqrt{5}[/latex]), a to nikako ne igra ulogu pored "tako jakog" člana kao [latex]2^{86+88n}[/latex]. Dakle, cijeli nazivnik zajedno izgleda kao [latex]\sqrt[88]{2^{86+88n}+3\cdot 2^{86+88n}}=\sqrt[88]{4\cdot 2^{86+88n}}=\sqrt[88]{2^{88+88n}}=2^{1+n}=2\cdot 2^n[/latex].
Stoga zaključujemo da je, budući da brojnik "izgleda kao" [latex]5\cdot 2^n[/latex], a nazivnik kao [latex]2\cdot 2^n[/latex], traženi limes jednak [latex]\displaystyle \frac{5\cdot 2^n}{2\cdot 2^n}=\frac{5}{2}[/latex].
I sad smo, vjerovao/la ili ne, manje-više gotovi. Glavno je da imamo ideju, nakon toga je sve dosta lagano - upravo ćemo doslovno iste stvari koje smo "zdravo seljački" objasnili gore pretvoriti u matematički ispravan argument.
Dakle, prvo ćemo i brojnik i nazivnik podijeliti s [latex]2^n[/latex] (jer smo shvatili da i jedno i drugo "otprilike izgleda" kao neka konstanta pomnožena s tim). Tada dobivamo da je traženi izraz jednak [latex]\displaystyle \frac{5+56\frac{n^4}{2^n}+\frac{n\sin(n)}{2^n}}{\sqrt[88]{\frac{2^{86+88n}}{2^{88n}}+3\frac{(n\cdot \frac{2^{43+44n}}{n+\sin(n)})^2}{2^{88n}}+\frac{\sqrt{\cos^2(n)+4}}{2^{88n}}}}[/latex].
OK, idemo sad član po član u brojniku: prvi član je konstanta, to je u redu. Drugi član ide u [latex]0[/latex], to ste i formalno dokazali na vježbama (da je eksponencijalna funkcija uvijek "puno jača" od polinoma), a i treći član isto. Naime, po teoremu o sendviču, [latex]-n\leq n\sin(n)\leq n[/latex], tj. [latex]\displaystyle -\frac{n}{2^n}\leq \frac{n\sin(n)}{2^n}\leq \frac{n}{2^n}[/latex], a i lijeva i desna strana idu u [latex]0[/latex] (ponovo iz argumenta s polinomom i eksponencijalnom funkcijom). Dakle, brojnik ide u [latex]5[/latex].
Pogledajmo nazivnik: Prvi član pod korijenom je konstanta, to je točno [latex]2^{86}[/latex]. Drugi član ćemo malo srediti i vidjeti da on iznosi [latex]\displaystyle 3\cdot 2^{86}\cdot (\frac{n}{n+\sin(n)})^2[/latex]. Kako očito vrijedi (iz definicije sinusa) [latex]\displaystyle \frac{n}{n-1}\leq \frac{n}{n+\sin(n)}\leq \frac{n}{n+1}[/latex], a i lijeva i desna strana idu u [latex]1[/latex], [latex](\frac{n}{n+\sin(n)})^2[/latex] ide u [latex]1^2=1[/latex], pa drugi član ide u [latex]3\cdot 2^{86}[/latex]. Ostaje još treći član. No, budući da vrijedi (po definiciji kosinusa) [latex]\displaystyle 0\leq \frac{\sqrt{\cos^2(n)+4}}{2^{88n}}\leq \frac{\sqrt{5}}{2^{88n}}[/latex], a i lijeva i desna strana idu u [latex]0[/latex] (tj. lijeva točno jest [latex]0[/latex]), zaključujemo po teoremu o sendviču da [latex]\frac{\sqrt{\cos^2(n)+4}}{2^{88n}}[/latex] ide u [latex]0[/latex].
I to je to - zbog neprekidnosti [latex]88[/latex]-og korijena, nazivnik ide u [latex]\sqrt[88]{2^{86}+3\cdot 2^{86}+0}=2[/latex], pa je i limes cijelog niza [latex]\frac{5}{2}[/latex], dakle, upravo ono što smo utvrdili "zdravo seljački".
Nadam se da sam ovime pokazao ideju kojom se ja vodim prilikom rješavanja ovakvih zadataka. Moje isprike što sam te izvrgao zaista krajnjoj gnjusobi od zadatka, ali uzmi u obzir da sam ga ja smislio - zamisli samo kako je meni teško živjeti sa mnom svaki dan :D.
I sad ti se vjerojatno tvoj zadatak ne čini ni toliko čudan ni toliko težak :). Dakle, svaki od članova u sumi "izgleda kao" [latex]\displaystyle \frac{1}{n^2}[/latex]: brojnik je [latex]1[/latex], a u nazivniku imamo nešto između [latex]n^2[/latex] i [latex]n^2+n[/latex]. Ovaj drugi pribrojnik u nazivniku je svakako manji (tj. manji ili jednak) od [latex]n[/latex], a kako [latex]n^2[/latex] raste "puno brže" od [latex]n[/latex], jasno nam je (opet "zdravo seljački", ne matematički) da ga možemo zanemariti. Stoga, ti tu imaš, zapravo, sumu [latex]n[/latex] brojeva koji svi izgledaju kao [latex]\displaystyle \frac{1}{n^2}[/latex]. Dakle, ta suma izgleda kao [latex]\displaystyle n\cdot \frac{1}{n^2}[/latex] - odavde ideja da uspoređujemo s [latex]\displaystyle \frac{1}{n}[/latex], što se i pokazuje točnim u formalnom matematičkom računu kojeg sam prije izveo.
Nekako se jako puno zadataka (nešto manje njih sa sumama, oni znaju biti malo atipični, ali u ovom zadatku smo imali sreću) da sagledati na ovakav način - dakle, osnovnu ideju steknemo i prije nego što počnemo ozbiljno pisati pravi dokaz, a taj dokaz nam je onda relativno lagan i jasan jer smo već prije isplanirali što ćemo sve napraviti.
(Upozorenje: Ovo će biti dugo  . Među ostalim i jer su, bar meni, takve stvari dosta zanimljive. Vjerojatno će ti trebati papir ako planiraš pomno pratiti . Među ostalim i jer su, bar meni, takve stvari dosta zanimljive. Vjerojatno će ti trebati papir ako planiraš pomno pratiti  .) .)
Nešto slično sam napisao već u prethodnom postu. Uglavnom, po mom je mišljenju u ovakvim zadacima intuicija dosta bitna stvar, bitnija od učenja čistih šablona za rješavanje zadataka. Naime, onda se pojavi ovakav zadatak kakav se tebi pojavio, koji se nije puno obrađivao na vježbama i čovjek ostane zbunjen. Tu, pod "intuicija" mislim na "kako se nešto ponaša", tj. "čemu jednostavnome to sliči". To se upravo pojavljuje u tvom zadatku - poanta je da shvatiš koliko ima pribrojnika i kako svaki od njih "izgleda".
Da dam jedan nasumični primjer (nije sa sumama, ali je ideja koju želim pokazati ista) - zanima nas 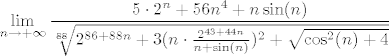 . Jest, izraz je krajnje gnjusan (a nazivnik pomalo namješten . Jest, izraz je krajnje gnjusan (a nazivnik pomalo namješten  ). Upravo zato, pogledajmo prvo "zdravo seljački" kako se ponašaju brojnik i nazivnik, a onda ćemo odlučiti kako dalje. Nemoj da te buni ako nisi siguran/na kako bi ga riješio/la iz prve - zadatak je namjerno vrijedan prezira, zato da pokažem princip na ekstremnom primjeru kojeg je teško čak i za napisati, ali začudo neće biti toliko teško za shvatiti ideju rješenja. ). Upravo zato, pogledajmo prvo "zdravo seljački" kako se ponašaju brojnik i nazivnik, a onda ćemo odlučiti kako dalje. Nemoj da te buni ako nisi siguran/na kako bi ga riješio/la iz prve - zadatak je namjerno vrijedan prezira, zato da pokažem princip na ekstremnom primjeru kojeg je teško čak i za napisati, ali začudo neće biti toliko teško za shvatiti ideju rješenja.
Primijetit ćeš da je sve ovo što radimo upravo kako sam rekao - "zdravo seljački", što bi reklo da, makar jest u biti točno, nikako nije dovoljno rigorozno da se može prihvatiti kao legalni dokaz. Do tog dijela ćemo doći kasnije. OK, dakle, otprilike ovako razmišljamo:
Primijetimo da je  uvjerljivo "najjači" član u brojniku: uvjerljivo "najjači" član u brojniku: 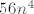 raste puno sporije nego raste puno sporije nego  , a , a 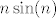 se ponaša "negdje između" se ponaša "negdje između"  i i  , što je u svakom slučaju dovoljno malo da ne igra ulogu na sumu u kojoj sudjeluje , što je u svakom slučaju dovoljno malo da ne igra ulogu na sumu u kojoj sudjeluje 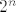 (tj. (tj.  - znamo da nam konstanta baš ni ne utječe na "red veličine" brzine rasta, da ju množi s tom konstantom). Stoga, brojnik otprilike izgleda kao - znamo da nam konstanta baš ni ne utječe na "red veličine" brzine rasta, da ju množi s tom konstantom). Stoga, brojnik otprilike izgleda kao  . .
Pogledajmo nazivnik. Imamo 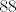 -i korijen od svega, pa pogledajmo prvo što je ispod tog korijena. Vidimo da u sumi sudjeluje -i korijen od svega, pa pogledajmo prvo što je ispod tog korijena. Vidimo da u sumi sudjeluje 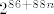 , što raste jako brzo. Sad, primijetimo da drugi pribrojnik, tj. , što raste jako brzo. Sad, primijetimo da drugi pribrojnik, tj. 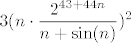 izgleda otprilike kao izgleda otprilike kao 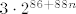 . To argumentiramo ovako: . To argumentiramo ovako: 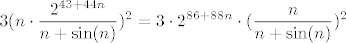 . Ovaj zadnji razlomak (pod kvadratom) ima brojnik . Ovaj zadnji razlomak (pod kvadratom) ima brojnik  , a nazivnik isto "izgleda kao" , a nazivnik isto "izgleda kao"  . Naime, . Naime, 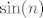 je između je između  i i  , a to "u beskonačnosti" i ne igra nekakvu ulogu kad se zbroji s , a to "u beskonačnosti" i ne igra nekakvu ulogu kad se zbroji s  . Dakle, . Dakle, 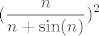 će izgledati kao će izgledati kao 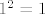 , pa će i , pa će i 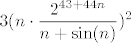 izgledati kao izgledati kao 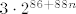 . Preostaje nam još korijen od ovog izraza s kosinusom, ali to nam i nije neki problem: kako je kosinus između . Preostaje nam još korijen od ovog izraza s kosinusom, ali to nam i nije neki problem: kako je kosinus između  i i  , onda će i ovaj korijen biti ograničen (bit će između , onda će i ovaj korijen biti ograničen (bit će između 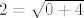 i i 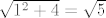 ), a to nikako ne igra ulogu pored "tako jakog" člana kao ), a to nikako ne igra ulogu pored "tako jakog" člana kao 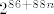 . Dakle, cijeli nazivnik zajedno izgleda kao . Dakle, cijeli nazivnik zajedno izgleda kao 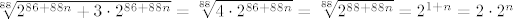 . .
Stoga zaključujemo da je, budući da brojnik "izgleda kao"  , a nazivnik kao , a nazivnik kao  , traženi limes jednak , traženi limes jednak 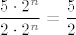 . .
I sad smo, vjerovao/la ili ne, manje-više gotovi. Glavno je da imamo ideju, nakon toga je sve dosta lagano - upravo ćemo doslovno iste stvari koje smo "zdravo seljački" objasnili gore pretvoriti u matematički ispravan argument.
Dakle, prvo ćemo i brojnik i nazivnik podijeliti s 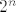 (jer smo shvatili da i jedno i drugo "otprilike izgleda" kao neka konstanta pomnožena s tim). Tada dobivamo da je traženi izraz jednak (jer smo shvatili da i jedno i drugo "otprilike izgleda" kao neka konstanta pomnožena s tim). Tada dobivamo da je traženi izraz jednak 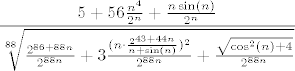 . .
OK, idemo sad član po član u brojniku: prvi član je konstanta, to je u redu. Drugi član ide u  , to ste i formalno dokazali na vježbama (da je eksponencijalna funkcija uvijek "puno jača" od polinoma), a i treći član isto. Naime, po teoremu o sendviču, , to ste i formalno dokazali na vježbama (da je eksponencijalna funkcija uvijek "puno jača" od polinoma), a i treći član isto. Naime, po teoremu o sendviču, 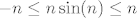 , tj. , tj. 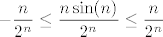 , a i lijeva i desna strana idu u , a i lijeva i desna strana idu u  (ponovo iz argumenta s polinomom i eksponencijalnom funkcijom). Dakle, brojnik ide u (ponovo iz argumenta s polinomom i eksponencijalnom funkcijom). Dakle, brojnik ide u  . .
Pogledajmo nazivnik: Prvi član pod korijenom je konstanta, to je točno 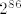 . Drugi član ćemo malo srediti i vidjeti da on iznosi . Drugi član ćemo malo srediti i vidjeti da on iznosi 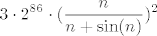 . Kako očito vrijedi (iz definicije sinusa) . Kako očito vrijedi (iz definicije sinusa) 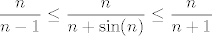 , a i lijeva i desna strana idu u , a i lijeva i desna strana idu u  , , 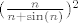 ide u ide u 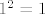 , pa drugi član ide u , pa drugi član ide u 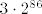 . Ostaje još treći član. No, budući da vrijedi (po definiciji kosinusa) . Ostaje još treći član. No, budući da vrijedi (po definiciji kosinusa) 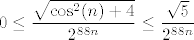 , a i lijeva i desna strana idu u , a i lijeva i desna strana idu u  (tj. lijeva točno jest (tj. lijeva točno jest  ), zaključujemo po teoremu o sendviču da ), zaključujemo po teoremu o sendviču da 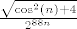 ide u ide u  . .
I to je to - zbog neprekidnosti 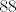 -og korijena, nazivnik ide u -og korijena, nazivnik ide u 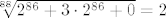 , pa je i limes cijelog niza , pa je i limes cijelog niza 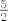 , dakle, upravo ono što smo utvrdili "zdravo seljački". , dakle, upravo ono što smo utvrdili "zdravo seljački".
Nadam se da sam ovime pokazao ideju kojom se ja vodim prilikom rješavanja ovakvih zadataka. Moje isprike što sam te izvrgao zaista krajnjoj gnjusobi od zadatka, ali uzmi u obzir da sam ga ja smislio - zamisli samo kako je meni teško živjeti sa mnom svaki dan  . .
I sad ti se vjerojatno tvoj zadatak ne čini ni toliko čudan ni toliko težak  . Dakle, svaki od članova u sumi "izgleda kao" . Dakle, svaki od članova u sumi "izgleda kao" 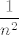 : brojnik je : brojnik je  , a u nazivniku imamo nešto između , a u nazivniku imamo nešto između 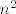 i i 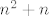 . Ovaj drugi pribrojnik u nazivniku je svakako manji (tj. manji ili jednak) od . Ovaj drugi pribrojnik u nazivniku je svakako manji (tj. manji ili jednak) od  , a kako , a kako 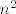 raste "puno brže" od raste "puno brže" od  , jasno nam je (opet "zdravo seljački", ne matematički) da ga možemo zanemariti. Stoga, ti tu imaš, zapravo, sumu , jasno nam je (opet "zdravo seljački", ne matematički) da ga možemo zanemariti. Stoga, ti tu imaš, zapravo, sumu  brojeva koji svi izgledaju kao brojeva koji svi izgledaju kao 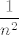 . Dakle, ta suma izgleda kao . Dakle, ta suma izgleda kao 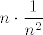 - odavde ideja da uspoređujemo s - odavde ideja da uspoređujemo s  , što se i pokazuje točnim u formalnom matematičkom računu kojeg sam prije izveo. , što se i pokazuje točnim u formalnom matematičkom računu kojeg sam prije izveo.
Nekako se jako puno zadataka (nešto manje njih sa sumama, oni znaju biti malo atipični, ali u ovom zadatku smo imali sreću) da sagledati na ovakav način - dakle, osnovnu ideju steknemo i prije nego što počnemo ozbiljno pisati pravi dokaz, a taj dokaz nam je onda relativno lagan i jasan jer smo već prije isplanirali što ćemo sve napraviti.
|
|
| [Vrh] |
|
niveus
Forumaš(ica)

Pridružen/a: 26. 10. 2009. (16:12:58)
Postovi: (5E)16
|
|
| [Vrh] |
|
|









