| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
satja
Forumaš(ica)

Pridružen/a: 16. 05. 2010. (10:44:17)
Postovi: (F1)16
|
 Postano: 9:52 pon, 2. 1. 2012 Naslov: Postano: 9:52 pon, 2. 1. 2012 Naslov: |
    |
|
|
Prvi limes ti je dobar i 33. ti je dobar i 34. ti je dobar i 37. ti je dobar.
Što se tiče ovog 36. zadatka, njega je riješio mornik na temi iz prošle godine, pa ću ga samo citirati.
[quote="mornik"]
Dakle, način na koji sam ja išao (ne jamčim da ne postoji bolji... dapače, začudio bih se da ne postoji :D): očito vrijedi [latex]a_{n+1}-a_n=\displaystyle\frac{1-2n}{2n}(a_n-a_{n-1})[/latex]. Teleskopiranjem, indukcijom ili kako već dolazimo lako do toga da je [latex]a_{n+1}-a_n=\displaystyle\frac{(1-2n)(3-2n)\cdots 3}{(2n)(2n-2)\cdots 4}(b-a)=\displaystyle\frac{2\cdot (-1)^{n-1}(2n-1)!!}{(2n)!!}[/latex]. (U ovom zapisu, [latex]k!!:=k\cdot (k-2)\cdot (k-4)\cdots[/latex], pri čemu je zadnji član u produktu [latex]2[/latex] ili [latex]1[/latex], ovisno o parnosti [latex]k[/latex]). Označimo, čisto radi lakšeg zapisa, s [latex]T(n)=\displaystyle\frac{2\cdot (-1)^n(2n+1)!!}{(2n+2)!!}[/latex].
E, sad, dolazi ovaj dio za koji baš i nemam objašnjenje. Kažem, moguće je da [latex]T_n[/latex] u sebi ima neki kombinatorni element, ali trenutno ga ne vidim. Nisam neko dulje vrijeme potrošio na ovo, pa je moguće da je očito, doduše.
U svakom slučaju, očito je dakle [latex]a_{n+1}=T(n-1)(b-a)+a_n=(T(n-1)+T(n-2))(b-a)+a_{n-1}[/latex]. Nastavljamo dalje, formalno indukcijom ili kako već, i dobivamo da je [latex]a_{n+1}=(T(n-1)+T(n-2)+\ldots+T(2)+T(1))(b-a)+a_2=(b-a)\displaystyle\sum_{i=1}^{n-1}T(i)+b[/latex].
No, sada ispada da je, iz meni trenutno nepoznatih razloga (iako je WolframAlpha uz minimalnu modifikaciju izbacila točan, simbolički, rezultat, pa pretpostavljam da se radi o nekoj verziji poznatog limesa koji možda ima, a možda nema veze s tzv. hipergeometrijskim funkcijama), [latex]\displaystyle\lim_{n}\sum_{i=1}^{n-1}T(i)=1-\sqrt{2}[/latex].
Stoga, ispada da je [latex]\displaystyle\lim_{n}a_n=(1-\sqrt{2})(b-a)+b=(2-\sqrt{2})b+(\sqrt{2}-1)a[/latex], baš kako si rekao. :)
Kažem, ja sam razumno uvjeren da je ovaj rezultat točan, ali u ovom trenutku ne mogu reći zašto je suma reda [latex]\sum T(n)[/latex] jednaka baš [latex]1-\sqrt{2}[/latex]. Ovaj prvi dio s gledanjem razlika susjednih članova niza mi se čini relativno bitnim za rješavanje ali, kažem, moguće, pa čak i vjerojatno, je da ima i boljih rješenja. :)[/quote]
Ovaj sa [tex]n^{p+1}[/tex] ću probati riješiti. Zapise iskaza o limesima i gomilištima pomoću logičkih simbola ste, nadam se, radili na predavanjima.
[size=9][color=#999999]Added after 8 minutes:[/color][/size]
I još nešto... Zenone, pitao si kako se možeš odužiti. Pa ja evo imam jednu ideju. Na ovom podforumu od analize ima puno tema s rješenjima raznih zadataka s kolokvija. Budući da se ekipa žalila što ne postoje rješenja kolokvija na webu, moguće je malo pogledati po tim starim temama i kopirati ta rješenja u TeX-u, a ona koja ne postoje, nadopisati (samo kratko, naravno, a i ne moraju biti svi riješeni), i tako možemo za buduće generacije ostaviti pdf-ove sa rješenjima bivših kolokvija. Tako bi studentima bilo lakše, a i demosi bi imali manje posla :).
Nemoj to raditi ako ti se ne da. Ali eto, budući da dosta svojih rješenja objavljuješ na forumu radi provjere, pomislio sam, da bi ti to možda rado napravio.
Prvi limes ti je dobar i 33. ti je dobar i 34. ti je dobar i 37. ti je dobar.
Što se tiče ovog 36. zadatka, njega je riješio mornik na temi iz prošle godine, pa ću ga samo citirati.
| mornik (napisa): |
Dakle, način na koji sam ja išao (ne jamčim da ne postoji bolji... dapače, začudio bih se da ne postoji  ): očito vrijedi ): očito vrijedi 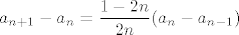 . Teleskopiranjem, indukcijom ili kako već dolazimo lako do toga da je . Teleskopiranjem, indukcijom ili kako već dolazimo lako do toga da je 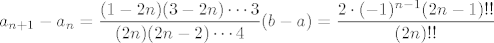 . (U ovom zapisu, . (U ovom zapisu, 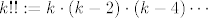 , pri čemu je zadnji član u produktu , pri čemu je zadnji član u produktu  ili ili  , ovisno o parnosti , ovisno o parnosti  ). Označimo, čisto radi lakšeg zapisa, s ). Označimo, čisto radi lakšeg zapisa, s 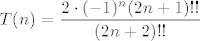 . .
E, sad, dolazi ovaj dio za koji baš i nemam objašnjenje. Kažem, moguće je da 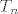 u sebi ima neki kombinatorni element, ali trenutno ga ne vidim. Nisam neko dulje vrijeme potrošio na ovo, pa je moguće da je očito, doduše. u sebi ima neki kombinatorni element, ali trenutno ga ne vidim. Nisam neko dulje vrijeme potrošio na ovo, pa je moguće da je očito, doduše.
U svakom slučaju, očito je dakle 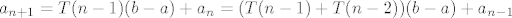 . Nastavljamo dalje, formalno indukcijom ili kako već, i dobivamo da je . Nastavljamo dalje, formalno indukcijom ili kako već, i dobivamo da je 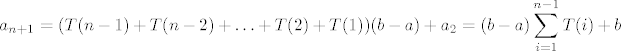 . .
No, sada ispada da je, iz meni trenutno nepoznatih razloga (iako je WolframAlpha uz minimalnu modifikaciju izbacila točan, simbolički, rezultat, pa pretpostavljam da se radi o nekoj verziji poznatog limesa koji možda ima, a možda nema veze s tzv. hipergeometrijskim funkcijama), 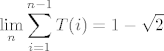 . .
Stoga, ispada da je 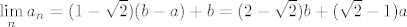 , baš kako si rekao. , baš kako si rekao. 
Kažem, ja sam razumno uvjeren da je ovaj rezultat točan, ali u ovom trenutku ne mogu reći zašto je suma reda 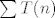 jednaka baš jednaka baš 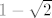 . Ovaj prvi dio s gledanjem razlika susjednih članova niza mi se čini relativno bitnim za rješavanje ali, kažem, moguće, pa čak i vjerojatno, je da ima i boljih rješenja. . Ovaj prvi dio s gledanjem razlika susjednih članova niza mi se čini relativno bitnim za rješavanje ali, kažem, moguće, pa čak i vjerojatno, je da ima i boljih rješenja.  |
Ovaj sa [tex]n^{p+1}[/tex] ću probati riješiti. Zapise iskaza o limesima i gomilištima pomoću logičkih simbola ste, nadam se, radili na predavanjima.
Added after 8 minutes:
I još nešto... Zenone, pitao si kako se možeš odužiti. Pa ja evo imam jednu ideju. Na ovom podforumu od analize ima puno tema s rješenjima raznih zadataka s kolokvija. Budući da se ekipa žalila što ne postoje rješenja kolokvija na webu, moguće je malo pogledati po tim starim temama i kopirati ta rješenja u TeX-u, a ona koja ne postoje, nadopisati (samo kratko, naravno, a i ne moraju biti svi riješeni), i tako možemo za buduće generacije ostaviti pdf-ove sa rješenjima bivših kolokvija. Tako bi studentima bilo lakše, a i demosi bi imali manje posla  . .
Nemoj to raditi ako ti se ne da. Ali eto, budući da dosta svojih rješenja objavljuješ na forumu radi provjere, pomislio sam, da bi ti to možda rado napravio.
|
|
| [Vrh] |
|
vsego
Site Admin


Pridružen/a: 06. 10. 2002. (22:07:09)
Postovi: (3562)16
Spol: 
Lokacija: /sbin/init
|
 Postano: 12:37 pon, 2. 1. 2012 Naslov: Postano: 12:37 pon, 2. 1. 2012 Naslov: |
    |
|
|
[quote="Zenon"]Ne znam riješiti:
Koristeći Cesaro-Stolzov teorem izračunajte:
[dtex]\lim_{n\to\infty}{\frac{1^p+2^p+\ldots +n^p}{n^{p+1}}},\quad p>1[/dtex]
Želim samo na glasiti da jedini uvijet na p je taj da je p>1, tj. [tex]p>1,p\in\mathbb R[/tex]. Pokušao sam svašta ali stalno dobijam ili 0-0, [tex]\frac 00[/tex], [tex]\infty -\infty[/tex] ili [tex]0\cdot\infty[/tex]... :([/quote]
Iskoristi teorem i dobit ces
[dtex]\lim_{n\to\infty} \frac{1^p+2^p+\ldots +n^p}{n^{p+1}} = \lim_{n\to\infty} \frac{(n+1)^p}{(n+1)^{p+1}-n^{p+1}}[/dtex]
Sada potencije suma raspises po [url=http://en.wikipedia.org/wiki/Binomial_theorem#Newton.27s_generalised_binomial_theorem]Newtonovom generaliziranom binomnom teoremu[/url]. U nazivniku ce se pokratiti [tex]n^{p+1}[/tex], pa ce ti ostati gore i dolje "polinomi" (navodnici jer potencije nisu nuzno cijele) s istom najvecom potencijom ([tex]n^p[/tex]), no s faktorom [tex]1[/tex] kod te potencije u brojniku i faktorom [tex]p+1[/tex] kod te potencije u nazivniku. Kad [tex]n \to \infty[/tex], ostale potencije se gube, pa ti ostane [tex]\frac{1}{p+1}[/tex].
Iskreno, ne da mi se to formalno raspisivati, pa taj dio prepustam tebi. O:)
| Zenon (napisa): | Ne znam riješiti:
Koristeći Cesaro-Stolzov teorem izračunajte:
[dtex]\lim_{n\to\infty}{\frac{1^p+2^p+\ldots +n^p}{n^{p+1}}},\quad p>1[/dtex]
Želim samo na glasiti da jedini uvijet na p je taj da je p>1, tj. [tex]p>1,p\in\mathbb R[/tex]. Pokušao sam svašta ali stalno dobijam ili 0-0, [tex]\frac 00[/tex], [tex]\infty -\infty[/tex] ili [tex]0\cdot\infty[/tex]...  |
Iskoristi teorem i dobit ces
[dtex]\lim_{n\to\infty} \frac{1^p+2^p+\ldots +n^p}{n^{p+1}} = \lim_{n\to\infty} \frac{(n+1)^p}{(n+1)^{p+1}-n^{p+1}}[/dtex]
Sada potencije suma raspises po Newtonovom generaliziranom binomnom teoremu. U nazivniku ce se pokratiti [tex]n^{p+1}[/tex], pa ce ti ostati gore i dolje "polinomi" (navodnici jer potencije nisu nuzno cijele) s istom najvecom potencijom ([tex]n^p[/tex]), no s faktorom [tex]1[/tex] kod te potencije u brojniku i faktorom [tex]p+1[/tex] kod te potencije u nazivniku. Kad [tex]n \to \infty[/tex], ostale potencije se gube, pa ti ostane [tex]\frac{1}{p+1}[/tex].
Iskreno, ne da mi se to formalno raspisivati, pa taj dio prepustam tebi. 
_________________ U pravilu ignoriram pitanja u krivim topicima i kodove koji nisu u [code]...[/code] blokovima.
Takodjer, OBJASNITE sto vas muci! "Sto mi je krivo?", bez opisa u cemu je problem, rijetko ce zadobiti moju paznju.  |
|
| [Vrh] |
|
Zenon
Forumaš(ica)


Pridružen/a: 09. 09. 2011. (19:14:43)
Postovi: (2B1)16
Sarma: -
Lokacija: [tex]\pm\infty[/tex]
|
 Postano: 15:54 pon, 2. 1. 2012 Naslov: Postano: 15:54 pon, 2. 1. 2012 Naslov: |
    |
|
|
[quote="satja"]
I još nešto... Zenone, pitao si kako se možeš odužiti. Pa ja evo imam jednu ideju. Na ovom podforumu od analize ima puno tema s rješenjima raznih zadataka s kolokvija. Budući da se ekipa žalila što ne postoje rješenja kolokvija na webu, moguće je malo pogledati po tim starim temama i kopirati ta rješenja u TeX-u, a ona koja ne postoje, nadopisati (samo kratko, naravno, a i ne moraju biti svi riješeni), i tako možemo za buduće generacije ostaviti pdf-ove sa rješenjima bivših kolokvija. Tako bi studentima bilo lakše, a i demosi bi imali manje posla :).
Nemoj to raditi ako ti se ne da. Ali eto, budući da dosta svojih rješenja objavljuješ na forumu radi provjere, pomislio sam, da bi ti to možda rado napravio.[/quote]
Mogu to napraviti, vrlo rado, ali tek poslije ovih kolokvija zato što sam vrlo pedantan i sve mora biti "tip top", pa ću na to vjerovatno potrošiti dosta vremena, a sada ga baš i nemam :P
Uvijek pomognem ako mogu, npr. na Arhimedesu, ali na ovom forumu više trebam pomoć nego što je mogu ponuditi :P
Tako da ću to napraviti kada prođu kolokviji i usmeni :)
Eto super.
[quote="vsego"]
Iskoristi teorem i dobit ces
[dtex]\lim_{n\to\infty} \frac{1^p+2^p+\ldots +n^p}{n^{p+1}} = \lim_{n\to\infty} \frac{(n+1)^p}{(n+1)^{p+1}-n^{p+1}}[/dtex]
Sada potencije suma raspises po [url=http://en.wikipedia.org/wiki/Binomial_theorem#Newton.27s_generalised_binomial_theorem]Newtonovom generaliziranom binomnom teoremu[/url]. U nazivniku ce se pokratiti [tex]n^{p+1}[/tex], pa ce ti ostati gore i dolje "polinomi" (navodnici jer potencije nisu nuzno cijele) s istom najvecom potencijom ([tex]n^p[/tex]), no s faktorom [tex]1[/tex] kod te potencije u brojniku i faktorom [tex]p+1[/tex] kod te potencije u nazivniku. Kad [tex]n \to \infty[/tex], ostale potencije se gube, pa ti ostane [tex]\frac{1}{p+1}[/tex].
Iskreno, ne da mi se to formalno raspisivati, pa taj dio prepustam tebi. O:)[/quote]
Iskreno, ovo mi je sasvim dovoljno. ;) I da jeste, svejedno bih si ja raspisao sam tako da... :)
Puno hvala obojici!
:thankyou: :thankyou: :thankyou:
| satja (napisa): |
I još nešto... Zenone, pitao si kako se možeš odužiti. Pa ja evo imam jednu ideju. Na ovom podforumu od analize ima puno tema s rješenjima raznih zadataka s kolokvija. Budući da se ekipa žalila što ne postoje rješenja kolokvija na webu, moguće je malo pogledati po tim starim temama i kopirati ta rješenja u TeX-u, a ona koja ne postoje, nadopisati (samo kratko, naravno, a i ne moraju biti svi riješeni), i tako možemo za buduće generacije ostaviti pdf-ove sa rješenjima bivših kolokvija. Tako bi studentima bilo lakše, a i demosi bi imali manje posla  . .
Nemoj to raditi ako ti se ne da. Ali eto, budući da dosta svojih rješenja objavljuješ na forumu radi provjere, pomislio sam, da bi ti to možda rado napravio. |
Mogu to napraviti, vrlo rado, ali tek poslije ovih kolokvija zato što sam vrlo pedantan i sve mora biti "tip top", pa ću na to vjerovatno potrošiti dosta vremena, a sada ga baš i nemam 
Uvijek pomognem ako mogu, npr. na Arhimedesu, ali na ovom forumu više trebam pomoć nego što je mogu ponuditi 
Tako da ću to napraviti kada prođu kolokviji i usmeni 
Eto super.
| vsego (napisa): |
Iskoristi teorem i dobit ces
[dtex]\lim_{n\to\infty} \frac{1^p+2^p+\ldots +n^p}{n^{p+1}} = \lim_{n\to\infty} \frac{(n+1)^p}{(n+1)^{p+1}-n^{p+1}}[/dtex]
Sada potencije suma raspises po Newtonovom generaliziranom binomnom teoremu. U nazivniku ce se pokratiti [tex]n^{p+1}[/tex], pa ce ti ostati gore i dolje "polinomi" (navodnici jer potencije nisu nuzno cijele) s istom najvecom potencijom ([tex]n^p[/tex]), no s faktorom [tex]1[/tex] kod te potencije u brojniku i faktorom [tex]p+1[/tex] kod te potencije u nazivniku. Kad [tex]n \to \infty[/tex], ostale potencije se gube, pa ti ostane [tex]\frac{1}{p+1}[/tex].
Iskreno, ne da mi se to formalno raspisivati, pa taj dio prepustam tebi.  |
Iskreno, ovo mi je sasvim dovoljno.  I da jeste, svejedno bih si ja raspisao sam tako da... I da jeste, svejedno bih si ja raspisao sam tako da... 
Puno hvala obojici!
  
|
|
| [Vrh] |
|
PermutiranoPrase
Forumaš(ica)


Pridružen/a: 10. 09. 2011. (16:08:19)
Postovi: (F4)16
Spol: 
|
|
| [Vrh] |
|
quark
Forumaš(ica)


Pridružen/a: 22. 10. 2011. (16:47:39)
Postovi: (DA)16
Spol: 
|
|
| [Vrh] |
|
PermutiranoPrase
Forumaš(ica)


Pridružen/a: 10. 09. 2011. (16:08:19)
Postovi: (F4)16
Spol: 
|
|
| [Vrh] |
|
room
Forumaš(ica)

Pridružen/a: 03. 11. 2013. (15:41:40)
Postovi: (78)16
Spol: 
|
 Postano: 0:03 pon, 6. 1. 2014 Naslov: Postano: 0:03 pon, 6. 1. 2014 Naslov: |
    |
|
|
Imam par pitanja iz skripte sa weba ([url]http://web.math.pmf.unizg.hr/nastava/analiza/files/nizovi2.pdf[/url]) i iz treće zadaće ([url]http://web.math.pmf.unizg.hr/nastava/analiza/files/ma1-zadaca3.pdf[/url])
Iz zadaće 1 pod b). Treba dokazati da je strogo padajući. Jel ja tu trebam samo dokazati da je [tex]a_n > a_{n+1}[/tex] ? Jer ako da, onda sam se nešto zapetljala u raspisivanju pa ću pokušati ponovno.
Onda 2 pod b) i c). Pod b) me zanima što se treba dobiti jer nisam sigurna da sam dobro dobila jer mislim da sam negdje na forumu vidjela nešto drugačije. A pod c) ne znam kako bi uopće (i to sam isto vidjela negdje na forumu, ali nisam neko dobro objašnjenje našla ili ga bar ja nisam shvatila..)
9 a), ne znam kako bi trebalo ići to sa četvrtim korijenom..
A što se skripte tiče, 2.9. pod d) i f). Jednostavni su zadaci, ali me zanima da li ima (tj. znam da ima) neki jednostavniji način rješavanja ovoga, a da ne moram raspisivati sve?
2.10. c) bi mi trebao hint, znam da će ići nekako pomoću teorema o sendviču.
2.28. b) objašnjenje jer ga ne shvaćam, zašto smo uopće sad tu uveli ln? (to je prvo pitanje, iako mi ni onda dalje neki djelići nisu jasni)
--
Ako bi itko išta od ovoga mogao riješiti ili objasniti, bila bih mu zahvalna. :)
Imam par pitanja iz skripte sa weba (http://web.math.pmf.unizg.hr/nastava/analiza/files/nizovi2.pdf) i iz treće zadaće (http://web.math.pmf.unizg.hr/nastava/analiza/files/ma1-zadaca3.pdf)
Iz zadaće 1 pod b). Treba dokazati da je strogo padajući. Jel ja tu trebam samo dokazati da je [tex]a_n > a_{n+1}[/tex] ? Jer ako da, onda sam se nešto zapetljala u raspisivanju pa ću pokušati ponovno.
Onda 2 pod b) i c). Pod b) me zanima što se treba dobiti jer nisam sigurna da sam dobro dobila jer mislim da sam negdje na forumu vidjela nešto drugačije. A pod c) ne znam kako bi uopće (i to sam isto vidjela negdje na forumu, ali nisam neko dobro objašnjenje našla ili ga bar ja nisam shvatila..)
9 a), ne znam kako bi trebalo ići to sa četvrtim korijenom..
A što se skripte tiče, 2.9. pod d) i f). Jednostavni su zadaci, ali me zanima da li ima (tj. znam da ima) neki jednostavniji način rješavanja ovoga, a da ne moram raspisivati sve?
2.10. c) bi mi trebao hint, znam da će ići nekako pomoću teorema o sendviču.
2.28. b) objašnjenje jer ga ne shvaćam, zašto smo uopće sad tu uveli ln? (to je prvo pitanje, iako mi ni onda dalje neki djelići nisu jasni)
–
Ako bi itko išta od ovoga mogao riješiti ili objasniti, bila bih mu zahvalna. 
|
|
| [Vrh] |
|
|









