| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
michelle.magenta
Forumaš(ica)

Pridružen/a: 18. 09. 2007. (22:48:47)
Postovi: (A)16
Lokacija: Zagreb
|
 Postano: 19:56 sri, 10. 10. 2007 Naslov: Dokaz da je broj iracionalan Postano: 19:56 sri, 10. 10. 2007 Naslov: Dokaz da je broj iracionalan |
    |
|
|
Na vježbama smo radili primjere tipa dokaži da je [latex]${\footnotesize\sqrt{7}}$[/latex] iracionalan broj.
Meni je taj dokaz savršeno jasan, međutim tračak sumnje ulila mi je činjenica da za [latex]${\small\sqrt{4}}$[/latex] na kraju isto dobivam kontradikciju s početnom pretpostavkom... odn. M(m,n)[latex]\neq[/latex]1
Zašto se matematika nije pobrinula i za to, odnosno moje pitanje je radim li što krivo? Po ovoj šabloni je i broj 2 iracionalan.
Mogu ja i cijeli postupak napisati kako sam završio na kontradikciji s pretpostavkom, međutim ne vladam baš još latexom toliko. Neka netko proba, pretpostavljam da postoji neko trivijalno objašnjenje.
Na vježbama smo radili primjere tipa dokaži da je 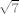 iracionalan broj. iracionalan broj.
Meni je taj dokaz savršeno jasan, međutim tračak sumnje ulila mi je činjenica da za 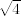 na kraju isto dobivam kontradikciju s početnom pretpostavkom... odn. M(m,n) na kraju isto dobivam kontradikciju s početnom pretpostavkom... odn. M(m,n)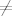 1 1
Zašto se matematika nije pobrinula i za to, odnosno moje pitanje je radim li što krivo? Po ovoj šabloni je i broj 2 iracionalan.
Mogu ja i cijeli postupak napisati kako sam završio na kontradikciji s pretpostavkom, međutim ne vladam baš još latexom toliko. Neka netko proba, pretpostavljam da postoji neko trivijalno objašnjenje.
Zadnja promjena: michelle.magenta; 20:05 sri, 10. 10. 2007; ukupno mijenjano 1 put.
|
|
| [Vrh] |
|
Novi
Forumaš(ica)

Pridružen/a: 17. 07. 2007. (12:08:32)
Postovi: (11F)16
Spol: 
|
|
| [Vrh] |
|
michelle.magenta
Forumaš(ica)

Pridružen/a: 18. 09. 2007. (22:48:47)
Postovi: (A)16
Lokacija: Zagreb
|
|
| [Vrh] |
|
|





