| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
punio4
Forumaš(ica)


Pridružen/a: 08. 11. 2006. (18:32:34)
Postovi: (120)16
Spol: 
Lokacija: Zagreb
|
 Postano: 15:51 sub, 12. 1. 2008 Naslov: Limes niza Postano: 15:51 sub, 12. 1. 2008 Naslov: Limes niza |
    |
|
|
Evo sad baš čitam skriptu prof. Guljaša, i nije mi jasna definicija limesa niza:
[latex](\forall \varepsilon > 0), (\exists n_\varepsilon \in \mathbb{N}), (\forall n \in \mathbb{N}), ((n>n_\varepsilon) \Rightarrow (|a_n - a| < \varepsilon)[/latex]
Dakle... Za svaki [latex]\varepsilon[/latex] veći od 0 ([latex]\varepsilon \in \mathbb{R}[/latex] ili [latex]\mathbb{N}[/latex]?), postoji... e sad... što je taj [latex]n_\varepsilon[/latex]? Indeks ili baš broj?
Uglavnom, taj neki cijeli broj [latex]n_\varepsilon[/latex], takav da za svaki cijeli [latex]n[/latex], veći od tog [latex]n_\varepsilon[/latex] vrijedi da je udaljenost između [latex]a[/latex] i [latex]a_n[/latex] manja od [latex]\varepsilon[/latex]...
Uglavnom zmotan sam. Help?
Evo sad baš čitam skriptu prof. Guljaša, i nije mi jasna definicija limesa niza:
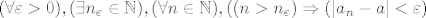
Dakle... Za svaki  veći od 0 ( veći od 0 (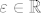 ili ili 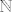 ?), postoji... e sad... što je taj ?), postoji... e sad... što je taj 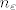 ? Indeks ili baš broj? ? Indeks ili baš broj?
Uglavnom, taj neki cijeli broj 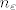 , takav da za svaki cijeli , takav da za svaki cijeli  , veći od tog , veći od tog 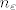 vrijedi da je udaljenost između vrijedi da je udaljenost između  i i 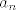 manja od manja od  ... ...
Uglavnom zmotan sam. Help?
|
|
| [Vrh] |
|
Luuka
Forumaš(ica)


Pridružen/a: 13. 02. 2007. (20:34:54)
Postovi: (925)16
Spol: 
Lokacija: Hakuna Matata
|
|
| [Vrh] |
|
punio4
Forumaš(ica)


Pridružen/a: 08. 11. 2006. (18:32:34)
Postovi: (120)16
Spol: 
Lokacija: Zagreb
|
|
| [Vrh] |
|
goranm
Forumaš(ica)


Pridružen/a: 12. 11. 2002. (20:09:12)
Postovi: (906)16
Spol: 
|
 Postano: 23:52 sub, 12. 1. 2008 Naslov: Re: Limes niza Postano: 23:52 sub, 12. 1. 2008 Naslov: Re: Limes niza |
    |
|
|
[quote="punio4"]što je taj [latex]n_\varepsilon[/latex]?[/quote]
Taj [latex]\epsilon[/latex] u [latex]n_\epsilon[/latex] je stavljen kako bi se naglasilo da [latex]n_\epsilon[/latex] ovisi o odabranom [latex]\epsilon[/latex]. Moglo je pisati i [latex](\forall \epsilon >0)(\exists m\in\mathbb{N})(\forall n\in\mathbb{N})(n>m) \dots[/latex]
Možda će ti topološka definicija konvergencije k točki biti jednostavnija za shvatiti:
Niz realnih brojeva [latex]x_1,x_2,x_3,\dots \in \mathbb{R}[/latex] konvergira k realnom broju [latex]x \in \mathbb{R}[/latex] ako za svaki interval [latex]\left\langle x- \epsilon,x+\epsilon\right\rangle[/latex] oko realnog broja [latex]x[/latex] postoji takav prirodan broj [latex]N[/latex] da svi članovi [latex]x_n[/latex] promatranog niza, za koje je [latex]n\geq N[/latex], pripadaju tom intervalu.
Dakle, koliko god mali intervalčić uzeo oko realnog broja [latex]x[/latex], uvijek će postojati dovoljno velik prirodan broj N tako da će se u tom intervalu nalaziti još svi oni članovi [latex]x_N,x_{N+1},\dots[/latex]
Ako malo raspišeš apsolutnu vrijednost u definiciji (iz analize), onda ćeš vidjeti da su te dvije definicije ekvivalentne. Ono što je u definiciji iz analize je:
[latex]|a_n-a|<\epsilon[/latex]
ili
[latex]-\epsilon<a_n - a <\epsilon[/latex]
[latex]a-\epsilon<a_n<a+\epsilon[/latex] , to jest
[latex]a_n \in \left\langle a-\epsilon,a+\epsilon \right \rangle[/latex].
| punio4 (napisa): | što je taj 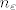 ? ? |
Taj  u u 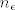 je stavljen kako bi se naglasilo da je stavljen kako bi se naglasilo da 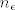 ovisi o odabranom ovisi o odabranom  . Moglo je pisati i . Moglo je pisati i 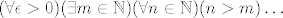
Možda će ti topološka definicija konvergencije k točki biti jednostavnija za shvatiti:
Niz realnih brojeva 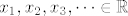 konvergira k realnom broju konvergira k realnom broju 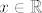 ako za svaki interval ako za svaki interval 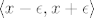 oko realnog broja oko realnog broja  postoji takav prirodan broj postoji takav prirodan broj 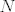 da svi članovi da svi članovi 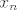 promatranog niza, za koje je promatranog niza, za koje je  , pripadaju tom intervalu. , pripadaju tom intervalu.
Dakle, koliko god mali intervalčić uzeo oko realnog broja  , uvijek će postojati dovoljno velik prirodan broj N tako da će se u tom intervalu nalaziti još svi oni članovi , uvijek će postojati dovoljno velik prirodan broj N tako da će se u tom intervalu nalaziti još svi oni članovi 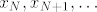
Ako malo raspišeš apsolutnu vrijednost u definiciji (iz analize), onda ćeš vidjeti da su te dvije definicije ekvivalentne. Ono što je u definiciji iz analize je:
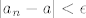
ili
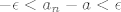
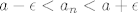 , to jest , to jest
 . .
_________________
The Dude Abides
|
|
| [Vrh] |
|
punio4
Forumaš(ica)


Pridružen/a: 08. 11. 2006. (18:32:34)
Postovi: (120)16
Spol: 
Lokacija: Zagreb
|
 Postano: 19:03 uto, 12. 2. 2008 Naslov: Postano: 19:03 uto, 12. 2. 2008 Naslov: |
    |
|
|
Evo, sad sam počeo raditi primjere, i nije mi npr jasan dokaz [latex]\lim_{n} \dfrac{1}{n} = 0[/latex]
[latex](\forall \varepsilon > 0), (\exists n_\varepsilon \in \mathbb{N}), (\forall n \in \mathbb{N}), ((n>n_\varepsilon) \Rightarrow (|a_n - a| < \varepsilon)[/latex]
Ok, prve 3 zagrade ostavimo sa strane, one su "univerzalne".
Ostane nam:
[latex](n>n_\varepsilon) \Rightarrow (|a_n - a| < \varepsilon)[/latex]
Modificiramo da vrijedi za ovaj niz:
[latex](n>n_\varepsilon) \Rightarrow (|\dfrac{1}{n} - 0| < \varepsilon)[/latex]
I dobili smo... Što :-k ?
[latex](n>n_\varepsilon) \Rightarrow (\dfrac{1}{n} < \varepsilon)[/latex]
Da je granična vrijednost < epsilon, a epsilon je > 0, dakle, da je granična vrijednost niza između nula i epsilon.
Da li smo time što dokazali? Mislim da ne.
Evo, sad sam počeo raditi primjere, i nije mi npr jasan dokaz 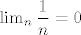
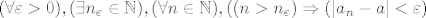
Ok, prve 3 zagrade ostavimo sa strane, one su "univerzalne".
Ostane nam:
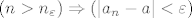
Modificiramo da vrijedi za ovaj niz:
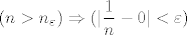
I dobili smo... Što  ? ?
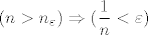
Da je granična vrijednost < epsilon, a epsilon je > 0, dakle, da je granična vrijednost niza između nula i epsilon.
Da li smo time što dokazali? Mislim da ne.
|
|
| [Vrh] |
|
Luuka
Forumaš(ica)


Pridružen/a: 13. 02. 2007. (20:34:54)
Postovi: (925)16
Spol: 
Lokacija: Hakuna Matata
|
|
| [Vrh] |
|
punio4
Forumaš(ica)


Pridružen/a: 08. 11. 2006. (18:32:34)
Postovi: (120)16
Spol: 
Lokacija: Zagreb
|
|
| [Vrh] |
|
nameless
Forumaš(ica)


Pridružen/a: 29. 09. 2007. (13:59:36)
Postovi: (58)16
Spol: 
Lokacija: Zagreb
|
 Postano: 19:56 uto, 12. 2. 2008 Naslov: Postano: 19:56 uto, 12. 2. 2008 Naslov: |
    |
|
|
[quote="punio4"]
Da li je onda *caka* u tome da zaključujemo:
Bez obzira koliko mali epsilon uzeli, 1/n je manji od njega, tj teži k nuli?
Ako da, čemu onda arhimed?[/quote]
pa nije caka.. koliki got mali epsilon uzeli, udaljenost od 1/n do 0 ce biti manja od njega nakon odredjenog n-a dakle kad epsilon tezi u 0, n epsilon tezi u besk,n tezi u besk, 1/n tezi u 0
| punio4 (napisa): |
Da li je onda *caka* u tome da zaključujemo:
Bez obzira koliko mali epsilon uzeli, 1/n je manji od njega, tj teži k nuli?
Ako da, čemu onda arhimed? |
pa nije caka.. koliki got mali epsilon uzeli, udaljenost od 1/n do 0 ce biti manja od njega nakon odredjenog n-a dakle kad epsilon tezi u 0, n epsilon tezi u besk,n tezi u besk, 1/n tezi u 0
_________________
"ja sam samo tu da vreme brže proleti"...
|
|
| [Vrh] |
|
Luuka
Forumaš(ica)


Pridružen/a: 13. 02. 2007. (20:34:54)
Postovi: (925)16
Spol: 
Lokacija: Hakuna Matata
|
|
| [Vrh] |
|
goranm
Forumaš(ica)


Pridružen/a: 12. 11. 2002. (20:09:12)
Postovi: (906)16
Spol: 
|
 Postano: 20:35 uto, 12. 2. 2008 Naslov: Postano: 20:35 uto, 12. 2. 2008 Naslov: |
    |
|
|
[quote="punio4"]
Da li je onda *caka* u tome da zaključujemo:
Bez obzira koliko mali epsilon uzeli, 1/n je manji od njega, tj teži k nuli?
Ako da, čemu onda arhimed?[/quote]
Arhimedov aksiom ti daje postojanje takvog broja [latex]n[/latex] za kojeg je [latex]\frac{1}{n}<\epsilon[/latex] , bez obzira o kojem se [latex]\epsilon[/latex]-u radilo.
Ključ je upravo u tri "univerzalne" zagrade koje si ostavio sastrane :) Definicija kaže da će limes od 1/n težiti k 0 ako, bez obzira koji epsilon odabrao, [u]postoji[/u] takav prirodan broj n tako da za svaki prirodan broj m veći od n vrijedi 1/m < e. Arhimedov aksiom kaže da takav broj stvarno postoji pa je onda limes 1/n = 0.
Kada ne bi imao Arhimedov aksiom, tada bi postojao barem jedan [latex]\epsilon > 0[/latex] takav da bi za sve prirodne brojeve n vrijedilo [latex]\frac{1}{n}\geq\epsilon[/latex] i tada 0 ne bi bila limes niza [latex](\frac{1}{n})_{n \in \mathbb{N}}[/latex].
| punio4 (napisa): |
Da li je onda *caka* u tome da zaključujemo:
Bez obzira koliko mali epsilon uzeli, 1/n je manji od njega, tj teži k nuli?
Ako da, čemu onda arhimed? |
Arhimedov aksiom ti daje postojanje takvog broja  za kojeg je za kojeg je 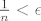 , bez obzira o kojem se , bez obzira o kojem se  -u radilo. -u radilo.
Ključ je upravo u tri "univerzalne" zagrade koje si ostavio sastrane  Definicija kaže da će limes od 1/n težiti k 0 ako, bez obzira koji epsilon odabrao, postoji takav prirodan broj n tako da za svaki prirodan broj m veći od n vrijedi 1/m < e. Arhimedov aksiom kaže da takav broj stvarno postoji pa je onda limes 1/n = 0. Definicija kaže da će limes od 1/n težiti k 0 ako, bez obzira koji epsilon odabrao, postoji takav prirodan broj n tako da za svaki prirodan broj m veći od n vrijedi 1/m < e. Arhimedov aksiom kaže da takav broj stvarno postoji pa je onda limes 1/n = 0.
Kada ne bi imao Arhimedov aksiom, tada bi postojao barem jedan 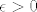 takav da bi za sve prirodne brojeve n vrijedilo takav da bi za sve prirodne brojeve n vrijedilo 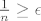 i tada 0 ne bi bila limes niza i tada 0 ne bi bila limes niza 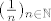 . .
_________________
The Dude Abides
|
|
| [Vrh] |
|
|














