| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
StateOfConsciousness
Forumaš s poteškoćama u pisanju


Pridružen/a: 22. 07. 2008. (16:08:24)
Postovi: (8A)16
|
|
| [Vrh] |
|
Luuka
Forumaš(ica)


Pridružen/a: 13. 02. 2007. (20:34:54)
Postovi: (925)16
Spol: 
Lokacija: Hakuna Matata
|
|
| [Vrh] |
|
goranm
Forumaš(ica)


Pridružen/a: 12. 11. 2002. (20:09:12)
Postovi: (906)16
Spol: 
|
 Postano: 23:30 sri, 6. 8. 2008 Naslov: Postano: 23:30 sri, 6. 8. 2008 Naslov: |
    |
|
|
U Aignerovoj i Zieglerovoj knjizi [i]Proofs from The Book[/i] predstavljeno je 6 dokaza; meni je najdraži Furstenbergov, no budući je već naveden, prepisati ću Goldbachov:
Promotrimo Fermatove brojeve [latex]F_n = 2^{2^n}+1[/latex], gdje je n nenegativan cijeli broj. Pokazati ćemo da su svaka dva Fermatova broja relativno prosta; iz toga slijedi da prostih brojeva mora biti beskonačno mnogo.
Promotrimo rekurziju [latex]\displaystyle\prod_{k=0}^{n-1}F_k = F_n - 2[/latex], gdje je n prirodan broj (sama rekurzija se jednostavno dokazuje indukcijom). Ako m dijeli [latex]F_k[/latex] i [latex]F_n[/latex], tada m dijeli 2 pa slijedi da je m jednak ili 1 ili 2. No m ne može biti 2 jer su svi Fermatovi brojevi neparni. Dakle, svaka dva Fermatova broja su relativno prosta.
Preostali dokazi u [i]Knjizi[/i] su Euklidov, Eulerov i Erdosov te jedan algebarski koji se smatra narodnim folklorom. :)
U Aignerovoj i Zieglerovoj knjizi Proofs from The Book predstavljeno je 6 dokaza; meni je najdraži Furstenbergov, no budući je već naveden, prepisati ću Goldbachov:
Promotrimo Fermatove brojeve 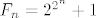 , gdje je n nenegativan cijeli broj. Pokazati ćemo da su svaka dva Fermatova broja relativno prosta; iz toga slijedi da prostih brojeva mora biti beskonačno mnogo. , gdje je n nenegativan cijeli broj. Pokazati ćemo da su svaka dva Fermatova broja relativno prosta; iz toga slijedi da prostih brojeva mora biti beskonačno mnogo.
Promotrimo rekurziju 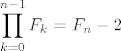 , gdje je n prirodan broj (sama rekurzija se jednostavno dokazuje indukcijom). Ako m dijeli , gdje je n prirodan broj (sama rekurzija se jednostavno dokazuje indukcijom). Ako m dijeli 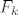 i i 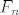 , tada m dijeli 2 pa slijedi da je m jednak ili 1 ili 2. No m ne može biti 2 jer su svi Fermatovi brojevi neparni. Dakle, svaka dva Fermatova broja su relativno prosta. , tada m dijeli 2 pa slijedi da je m jednak ili 1 ili 2. No m ne može biti 2 jer su svi Fermatovi brojevi neparni. Dakle, svaka dva Fermatova broja su relativno prosta.
Preostali dokazi u Knjizi su Euklidov, Eulerov i Erdosov te jedan algebarski koji se smatra narodnim folklorom. 
_________________
The Dude Abides
|
|
| [Vrh] |
|
alen
Forumaš(ica)


Pridružen/a: 14. 10. 2005. (23:25:58)
Postovi: (221)16
|
 Postano: 0:00 čet, 7. 8. 2008 Naslov: Postano: 0:00 čet, 7. 8. 2008 Naslov: |
    |
|
|
Ja ne vidim neku korist od dokazivanja neke tvrdnje na više načina osim ako se ne radi o bitno drukčijoj tehnici dokazivanja koja je znatno elegantnija.
Kom je dosadno, može probat dokazat da je [latex]\mathop {\lim }\limits_{n \to \infty } \sum\limits_{j = 0}^n {P\left( {X_n = j} \right)L_n^j } = 0[/latex], gdje je [latex]{X_n }[/latex] diskretna slučajna varijabla sa zakonom razdiobe [latex]P\left( {X_n = k} \right) = q\left( \begin{gathered}
n \hfill \\
k \hfill \\
\end{gathered} \right)\sum\limits_{i = 0}^k {\left( \begin{gathered}
k \hfill \\
i \hfill \\
\end{gathered} \right)\frac{{\left( { - 1} \right)^i \left( {1 - p} \right)^{n - k + i} }}
{{1 - \left( {1 - q} \right)\left( {1 - p} \right)^{n - k + i} }}} \cdot {\mathbf{1}}_{\left\{ {0,...,n} \right\}} \left( k \right)[/latex] i [latex]L_n : = 1 - \left( {P\left( {X_1 = 1} \right)} \right)^{\log _a n}[/latex] gdje je [latex]P\left( {X_1 = 1} \right) > a^{ - 1}[/latex] , [latex]a > 1[/latex] , [latex]p,q \in \left\langle {0,1} \right\rangle[/latex] (primjetite [latex]q \ne 1 - p[/latex]).
Vrijedi (već je dokazano) [latex]P\left( {X_1 = 1} \right) > a^{ - 1} \Rightarrow \mathop {\lim }\limits_{n \to \infty } L_n^n = 0[/latex] i [latex]Y_n \sim B\left( {n,p} \right) \Rightarrow \mathop {\lim }\limits_{n \to \infty } \frac{{P\left( {X_n = k} \right)}}
{{q \cdot P\left( {Y_n = k} \right)}} = 1[/latex], [latex]\forall k \in \mathbb{N}_0[/latex] .
Ja nisam uspio već 3 mjeseca pa ak neko zna... (lebegovi teoremi o konvergenciji baš nisu upalili jer nemogu nać s čim dominirat da bude integrabilno, a nije monoton niz)
Znači, za sad ima 0 dokaza ove tvrdnje pa ak neko navede samo jedan, to bi bilo sjajno
Ja ne vidim neku korist od dokazivanja neke tvrdnje na više načina osim ako se ne radi o bitno drukčijoj tehnici dokazivanja koja je znatno elegantnija.
Kom je dosadno, može probat dokazat da je 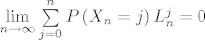 , gdje je , gdje je 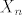 diskretna slučajna varijabla sa zakonom razdiobe diskretna slučajna varijabla sa zakonom razdiobe 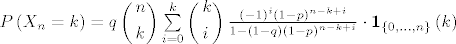 i i 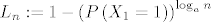 gdje je gdje je 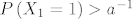 , , 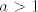 , , 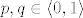 (primjetite (primjetite 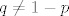 ). ).
Vrijedi (već je dokazano) 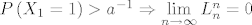 i i 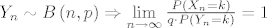 , , 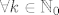 . .
Ja nisam uspio već 3 mjeseca pa ak neko zna... (lebegovi teoremi o konvergenciji baš nisu upalili jer nemogu nać s čim dominirat da bude integrabilno, a nije monoton niz)
Znači, za sad ima 0 dokaza ove tvrdnje pa ak neko navede samo jedan, to bi bilo sjajno
_________________
Između ostalog, mislim da bi kolegij mjera i integral trebao imati svoj podforum među kolegijima treće godine
Zadnja promjena: alen; 15:29 čet, 7. 8. 2008; ukupno mijenjano 1 put.
|
|
| [Vrh] |
|
Melkor
Forumaš(ica)


Pridružen/a: 07. 10. 2004. (18:48:00)
Postovi: (291)16
Spol: 
Lokacija: Void
|
|
| [Vrh] |
|
tantun
Forumaš(ica)


Pridružen/a: 17. 03. 2004. (22:32:32)
Postovi: (21)16
Spol: 
|
 Postano: 10:11 pet, 8. 8. 2008 Naslov: Postano: 10:11 pet, 8. 8. 2008 Naslov: |
    |
|
|
[quote="alen"]Ja ne vidim neku korist od dokazivanja neke tvrdnje na više načina osim ako se ne radi o bitno drukčijoj tehnici dokazivanja koja je znatno elegantnija.
Kom je dosadno, može probat dokazat da je [latex]\mathop {\lim }\limits_{n \to \infty } \sum\limits_{j = 0}^n {P\left( {X_n = j} \right)L_n^j } = 0[/latex], gdje je [latex]{X_n }[/latex] diskretna slučajna varijabla sa zakonom razdiobe [latex]P\left( {X_n = k} \right) = q\left( \begin{gathered}
n \hfill \\
k \hfill \\
\end{gathered} \right)\sum\limits_{i = 0}^k {\left( \begin{gathered}
k \hfill \\
i \hfill \\
\end{gathered} \right)\frac{{\left( { - 1} \right)^i \left( {1 - p} \right)^{n - k + i} }}
{{1 - \left( {1 - q} \right)\left( {1 - p} \right)^{n - k + i} }}} \cdot {\mathbf{1}}_{\left\{ {0,...,n} \right\}} \left( k \right)[/latex] i [latex]L_n : = 1 - \left( {P\left( {X_1 = 1} \right)} \right)^{\log _a n}[/latex] gdje je [latex]P\left( {X_1 = 1} \right) > a^{ - 1}[/latex] , [latex]a > 1[/latex] , [latex]p,q \in \left\langle {0,1} \right\rangle[/latex] (primjetite [latex]q \ne 1 - p[/latex]).
Vrijedi (već je dokazano) [latex]P\left( {X_1 = 1} \right) > a^{ - 1} \Rightarrow \mathop {\lim }\limits_{n \to \infty } L_n^n = 0[/latex] i [latex]Y_n \sim B\left( {n,p} \right) \Rightarrow \mathop {\lim }\limits_{n \to \infty } \frac{{P\left( {X_n = k} \right)}}
{{q \cdot P\left( {Y_n = k} \right)}} = 1[/latex], [latex]\forall k \in \mathbb{N}_0[/latex] .
Ja nisam uspio već 3 mjeseca pa ak neko zna... (lebegovi teoremi o konvergenciji baš nisu upalili jer nemogu nać s čim dominirat da bude integrabilno, a nije monoton niz)
Znači, za sad ima 0 dokaza ove tvrdnje pa ak neko navede samo jedan, to bi bilo sjajno[/quote]
Prvo uoci da ti konstanta [latex]q[/latex] nista ne znaci kao ni ovaj [latex]1-(1-q)(1-p)^{n-k+i}[/latex] u nazivniku (jer je ogranicen s [latex]q \leq 1-(1-q)(1-p)^{n-k+i} \leq 1[/latex] ). Drugim rijecima koristi [latex]P(X_n=k) \leq {\binom{n}{k}} \sum_{i=0}^k \binom{k}{i}(-1)^i(1-p)^{n-k+i}[/latex]. Tako da moras dokazati [latex]\lim_{n \to \infty} \sum_{k=0}^n \binom{n}{k} L_n^k\sum_{i=0}^k \binom{k}{i}(-1)^i(1-p)^{n-k+i}=0[/latex]. Sad raspisi
[latex]\sum_{i=0}^k \binom{k}{i}(-1)^i(1-p)^{n-k+i}=(1-p)^{n-k} \sum_{i=0}^k \binom{k}{i}(p-1)^{i}=(1-p)^{n-k}p^k[/latex] pa ti onaj izraz gore postaje [latex]\sum_{k=0}^n \binom{n}{k} L_n^k\sum_{i=0}^k \binom{k}{i}(-1)^i(1-p)^{n-k+i}= \sum_{k=0}^n \binom{n}{k}(L_np)^k(1-p)^{n-k}[/latex] sto je jednako [latex] (1-p+pL_n)^n[/latex]. Znaci samo moras dokazati [latex]\lim_{n \to \infty} (1-(1-L_n)p)^n = 0[/latex]. Oznaci [latex]t=P(X_n=1)[/latex] tada [latex](1-(1-L_n)p)^n=(1-pt^{\log_an})^n = ((1-pt^{\log_an})^{\frac{1}{pt^{\log_an}}})^{npt^{\log_an}}[/latex]. Sad [latex](1-pt^{\log_an})^{\frac{1}{pt^{\log_an}}} \to \frac{1}{e}[/latex] (jer ocito [latex]pt^{\log_an} \to 0[/latex]). Sad tvrdnja slijedi jer [latex]npt^{\log_an} \to \infty[/latex] a ovo je pak ocito ako uzmes logaritam dobijes [latex]\log p + \log n(1+\frac{\log t}{\log a}) \to \infty[/latex] jer je [latex]1+\frac{\log t}{\log a} > 0[/latex] (zbog uvjeta [latex]t > 1/a[/latex]).
Jel OK?
| alen (napisa): | Ja ne vidim neku korist od dokazivanja neke tvrdnje na više načina osim ako se ne radi o bitno drukčijoj tehnici dokazivanja koja je znatno elegantnija.
Kom je dosadno, može probat dokazat da je 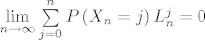 , gdje je , gdje je 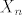 diskretna slučajna varijabla sa zakonom razdiobe diskretna slučajna varijabla sa zakonom razdiobe 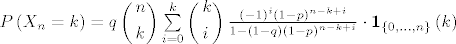 i i 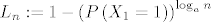 gdje je gdje je 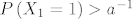 , , 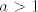 , , 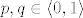 (primjetite (primjetite 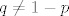 ). ).
Vrijedi (već je dokazano) 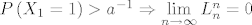 i i 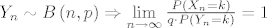 , , 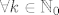 . .
Ja nisam uspio već 3 mjeseca pa ak neko zna... (lebegovi teoremi o konvergenciji baš nisu upalili jer nemogu nać s čim dominirat da bude integrabilno, a nije monoton niz)
Znači, za sad ima 0 dokaza ove tvrdnje pa ak neko navede samo jedan, to bi bilo sjajno |
Prvo uoci da ti konstanta  nista ne znaci kao ni ovaj nista ne znaci kao ni ovaj 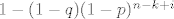 u nazivniku (jer je ogranicen s u nazivniku (jer je ogranicen s 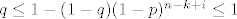 ). Drugim rijecima koristi ). Drugim rijecima koristi 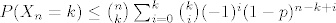 . Tako da moras dokazati . Tako da moras dokazati 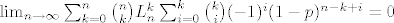 . Sad raspisi . Sad raspisi
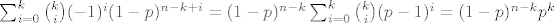 pa ti onaj izraz gore postaje pa ti onaj izraz gore postaje 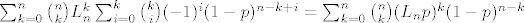 sto je jednako sto je jednako 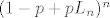 . Znaci samo moras dokazati . Znaci samo moras dokazati 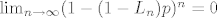 . Oznaci . Oznaci 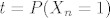 tada tada 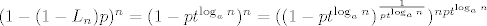 . Sad . Sad 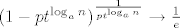 (jer ocito (jer ocito 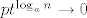 ). Sad tvrdnja slijedi jer ). Sad tvrdnja slijedi jer 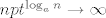 a ovo je pak ocito ako uzmes logaritam dobijes a ovo je pak ocito ako uzmes logaritam dobijes 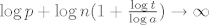 jer je jer je 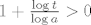 (zbog uvjeta (zbog uvjeta 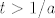 ). ).
Jel OK?
|
|
| [Vrh] |
|
alen
Forumaš(ica)


Pridružen/a: 14. 10. 2005. (23:25:58)
Postovi: (221)16
|
|
| [Vrh] |
|
alen
Forumaš(ica)


Pridružen/a: 14. 10. 2005. (23:25:58)
Postovi: (221)16
|
 Postano: 4:22 sri, 13. 8. 2008 Naslov: Postano: 4:22 sri, 13. 8. 2008 Naslov: |
    |
|
|
Zapravo, ipak ne valja, ne mora vrijediti [latex]P\left( {X_n = k} \right) \leqslant \left( \begin{gathered}
n \hfill \\
k \hfill \\
\end{gathered} \right)p^k \left( {1 - p} \right)^{n - k}[/latex] zbog [latex]\left( { - 1} \right)^i[/latex] u izrazu [latex]q\left( \begin{gathered}
n \hfill \\
k \hfill \\
\end{gathered} \right)\sum\limits_{i = 0}^k {\left( \begin{gathered}
k \hfill \\
i \hfill \\
\end{gathered} \right)\frac{{\left( { - 1} \right)^i \left( {1 - p} \right)^{n - k + i} }}
{{1 - \left( {1 - q} \right)\left( {1 - p} \right)^{n - k + i} }}}[/latex] (i općenito ne vrijedi [latex]P\left( {X_n = k} \right) \leqslant \left( \begin{gathered}
n \hfill \\
k \hfill \\
\end{gathered} \right)p^k \left( {1 - p} \right)^{n - k}[/latex])
EDIT: Upravo sam dokazo, ne trebate se više mučit, tantunu hvala na pomoći.
Zapravo, ipak ne valja, ne mora vrijediti 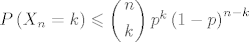 zbog zbog 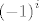 u izrazu u izrazu 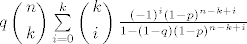 (i općenito ne vrijedi (i općenito ne vrijedi 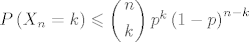 ) )
EDIT: Upravo sam dokazo, ne trebate se više mučit, tantunu hvala na pomoći.
_________________
Između ostalog, mislim da bi kolegij mjera i integral trebao imati svoj podforum među kolegijima treće godine
|
|
| [Vrh] |
|
|







