1. Odaberimo po volji neki prirodan broj m. Neka je [latex]n \leq m[/latex].
Ako je [latex]n=m[/latex], tada je potprostor [latex]\mathbb{R}^n(=\mathbb{R}^m)[/latex] cijeli prostor pa je po definiciji i zatvoren i otvoren potprostor prostora [latex]\mathbb{R}^m[/latex].
Neka je [latex]n<m[/latex]. Potprostor [latex]\mathbb{R}^n[/latex] je homeomorfan sa potprostorom [latex]S=\{ (x_1, x_2, \dots, x_n,0,\dots,0)~|~x_i \in \mathbb{R}, i=1,2,\dots,n\}\subset \mathbb{R}^m[/latex]. Odaberimo neku točku [b]x[/b] iz komplementa skupa S. Dovoljno je naći r>0 takav da je otvorena kugla sa središtem u točki [b]x[/b] i radijusom r sadržana u komplementu skupa S. Radijus r možemo uzeti na primjer kao pola udaljenosti od točke [b]x[/b] do njene ortogonalne projekcije [b]y[/b] u skupu S.
2. To da je taj skup vektorski potprostor slijedi iz toga da je zbroj neprekidnih funckija neprekidna funkcija i da je neprekidna funkcija pomnožena skalarom ponovo neprekidna. Onako definiran skalarni produkt će biti dobar ako zadovoljava [url=http://mathworld.wolfram.com/InnerProduct.html]definiciju skalarnog produkta[/url]. Svojstva integrala osiguravaju da će definicija biti zadovoljena (raspis je više manje trivijalan, a ne da mi se raspisivat ) :)
3. Budući je Y topološki potprostor od X, tada je svaki otvoren skup u Y oblika [latex]Y\cap W[/latex], gdje je W neki otvoren skup u X. Dakle, za otvoren [latex]V\subseteq Y[/latex] postoji otvoren W iz X takav da je [latex]V=Y\cap W[/latex]. Kako su i Y i W otvoreni u X, a konačan presjek otvorenih skupova je otvoren skup, tada je i V otvoren u X.
btw. ovi zadaci su više gradivo metričkih i/ili topoloških prostora nego analize 1 i 2. :)
1. Odaberimo po volji neki prirodan broj m. Neka je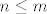 
.
Ako je 
, tada je potprostor 
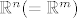cijeli prostor pa je po definiciji i zatvoren i otvoren potprostor prostora 
.
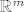Neka je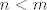 
. Potprostor 
je homeomorfan sa potprostorom 
. Odaberimo neku točku x iz komplementa skupa S. Dovoljno je naći r>0 takav da je otvorena kugla sa središtem u točki x i radijusom r sadržana u komplementu skupa S. Radijus r možemo uzeti na primjer kao pola udaljenosti od točke x do njene ortogonalne projekcije y u skupu S.
2. To da je taj skup vektorski potprostor slijedi iz toga da je zbroj neprekidnih funckija neprekidna funkcija i da je neprekidna funkcija pomnožena skalarom ponovo neprekidna. Onako definiran skalarni produkt će biti dobar ako zadovoljava definiciju skalarnog produkta. Svojstva integrala osiguravaju da će definicija biti zadovoljena (raspis je više manje trivijalan, a ne da mi se raspisivat ) 
3. Budući je Y topološki potprostor od X, tada je svaki otvoren skup u Y oblika 
, gdje je W neki otvoren skup u X. Dakle, za otvoren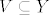 
postoji otvoren W iz X takav da je 
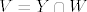. Kako su i Y i W otvoreni u X, a konačan presjek otvorenih skupova je otvoren skup, tada je i V otvoren u X.
btw. ovi zadaci su više gradivo metričkih i/ili topoloških prostora nego analize 1 i 2.
_________________
The Dude Abides
