|
Pretpostavljam da misliš na definiciju i Teorem 3.1. na 62. stranici (70. stranica u pdf formatu) [url=http://web.math.hr/~guljas/skripte/MATANALuR.pdf]skripte prof. Guljaša[/url].
Naravno, definicija neprekidnosti je na 68. stranici (76. u fileu), ali kao što piše u dokazu, direktno slijedi iz teorema koji sam spomenuo prije (samo uzmi [latex]L=f(c)[/latex], a nemoj da te zbunjuje to da u tom teoremu imamo nešto u stilu [latex]0<|x-c|<\delta[/latex], a u Cauchyjevoj definiciji neprekidnosti imamo [latex]|x-c|<\delta[/latex] - ako je [latex]|x-c|=0[/latex], onda je [latex]x=c[/latex], pa je [latex]|f(x)-f(c)|=0<\epsilon[/latex], tako da nam to ne igra ulogu).
Uglavnom, ako ti nešto u teoremu nije baš jasno, kako dolazimo do neke ideje ili tako nešto, pitaj, ovako mi je malo glupo samo prepisati teorem :). Ideja jednog smjera dokaza je naprosto da, koju god okolinu odabrali oko [latex]c[/latex], ako [latex]c_n\to c[/latex], nakon konačno mnogo članova, svi će ostali članovi niza [latex](c_n)_n[/latex] biti u toj okolini, a kako su svi elementi iz te okoline udaljeni za manje od [latex]\epsilon[/latex] od [latex]L[/latex], onda smo gotovi. To, zapravo, i jest cijeli dokaz, samo ga treba matematički precizno napisati. U drugom smjeru je ideja pretpostaviti suprotno i onda napraviti niz [latex](c_n)_n[/latex] takav da je [latex]\displaystyle |c_n-c|<\frac{1}{n}[/latex], a [latex]|f(c_n)-L|\geq\epsilon[/latex]. To je očita kontradikcija, pa smo gotovi. Ponovno, to treba matematički precizno napisati, ali to je to :). Još jednom, ako ti nešto nije jasno, pitaj, ovako je relativno besmisleno da samo prepišem skriptu :).
Pretpostavljam da misliš na definiciju i Teorem 3.1. na 62. stranici (70. stranica u pdf formatu) skripte prof. Guljaša.
Naravno, definicija neprekidnosti je na 68. stranici (76. u fileu), ali kao što piše u dokazu, direktno slijedi iz teorema koji sam spomenuo prije (samo uzmi 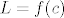 , a nemoj da te zbunjuje to da u tom teoremu imamo nešto u stilu , a nemoj da te zbunjuje to da u tom teoremu imamo nešto u stilu  , a u Cauchyjevoj definiciji neprekidnosti imamo , a u Cauchyjevoj definiciji neprekidnosti imamo 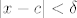 - ako je - ako je 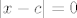 , onda je , onda je  , pa je , pa je 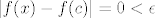 , tako da nam to ne igra ulogu). , tako da nam to ne igra ulogu).
Uglavnom, ako ti nešto u teoremu nije baš jasno, kako dolazimo do neke ideje ili tako nešto, pitaj, ovako mi je malo glupo samo prepisati teorem  . Ideja jednog smjera dokaza je naprosto da, koju god okolinu odabrali oko . Ideja jednog smjera dokaza je naprosto da, koju god okolinu odabrali oko  , ako , ako 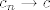 , nakon konačno mnogo članova, svi će ostali članovi niza , nakon konačno mnogo članova, svi će ostali članovi niza 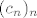 biti u toj okolini, a kako su svi elementi iz te okoline udaljeni za manje od biti u toj okolini, a kako su svi elementi iz te okoline udaljeni za manje od  od od  , onda smo gotovi. To, zapravo, i jest cijeli dokaz, samo ga treba matematički precizno napisati. U drugom smjeru je ideja pretpostaviti suprotno i onda napraviti niz , onda smo gotovi. To, zapravo, i jest cijeli dokaz, samo ga treba matematički precizno napisati. U drugom smjeru je ideja pretpostaviti suprotno i onda napraviti niz 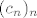 takav da je takav da je 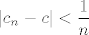 , a , a  . To je očita kontradikcija, pa smo gotovi. Ponovno, to treba matematički precizno napisati, ali to je to . To je očita kontradikcija, pa smo gotovi. Ponovno, to treba matematički precizno napisati, ali to je to  . Još jednom, ako ti nešto nije jasno, pitaj, ovako je relativno besmisleno da samo prepišem skriptu . Još jednom, ako ti nešto nije jasno, pitaj, ovako je relativno besmisleno da samo prepišem skriptu  . .
|









