| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
medonja
Forumaš(ica)


Pridružen/a: 20. 10. 2009. (17:01:04)
Postovi: (45)16
|
|
| [Vrh] |
|
c4rimson
Forumaš(ica)

Pridružen/a: 11. 01. 2010. (18:57:26)
Postovi: (3B)16
|
|
| [Vrh] |
|
vuja
Forumaš(ica)


Pridružen/a: 26. 09. 2009. (12:57:07)
Postovi: (2C)16
Spol: 
|
 Postano: 12:03 pet, 22. 1. 2010 Naslov: Re: Popravni kolokvij Postano: 12:03 pet, 22. 1. 2010 Naslov: Re: Popravni kolokvij |
    |
|
|
[quote="medonja"]http://web.math.hr/nastava/analiza/kol/ma1-0607-kp.pdf
dal netko moze rijesiti 3 zad iz ovog kolokvija...hvala..[/quote]
da bi dobio f(<0, ln5>) samo uvrstiš brojeve u funkciju. kad uvrstiš 0, dobiješ 1 - 8 + 12, što je jednako 5. kad uvrstiš ln5 dobiješ e^(2ln5) - 8e^(ln5) + 12. pošto ti je u eksponentu logaritam i baza logaritma jednaka bazi eksponencijalne fje, možeš spustiti eksponente i dobiješ 2ln5 - 8ln5 + 12 = 12 - 6 ln5 i to je cca 2.34, što je manje od 5. interval koji dobiješ je <12 - 6ln5, 5>. kad imaš prasliku na intervalu <-3, 0], znači da je f(x) iz tog intervala, odnosno da -3 < f(x) < 0. i rješavaš sustave dviju nejednadžbi, nađeš presjeke rješenja i to je konačno rješenje. ako ti je lakše, napraviš supstituciju e^x = t. nadam se da je ovo pomoglo :D
| medonja (napisa): | http://web.math.hr/nastava/analiza/kol/ma1-0607-kp.pdf
dal netko moze rijesiti 3 zad iz ovog kolokvija...hvala.. |
da bi dobio f(<0, ln5>) samo uvrstiš brojeve u funkciju. kad uvrstiš 0, dobiješ 1 - 8 + 12, što je jednako 5. kad uvrstiš ln5 dobiješ e^(2ln5) - 8e^(ln5) + 12. pošto ti je u eksponentu logaritam i baza logaritma jednaka bazi eksponencijalne fje, možeš spustiti eksponente i dobiješ 2ln5 - 8ln5 + 12 = 12 - 6 ln5 i to je cca 2.34, što je manje od 5. interval koji dobiješ je <12 - 6ln5, 5>. kad imaš prasliku na intervalu ←3, 0], znači da je f(x) iz tog intervala, odnosno da -3 < f(x) < 0. i rješavaš sustave dviju nejednadžbi, nađeš presjeke rješenja i to je konačno rješenje. ako ti je lakše, napraviš supstituciju e^x = t. nadam se da je ovo pomoglo 
|
|
| [Vrh] |
|
jkrstic
Forumaš(ica)


Pridružen/a: 01. 10. 2009. (19:28:31)
Postovi: (AC)16
Spol: 
Lokacija: Somewhere in time
|
 Postano: 12:13 pet, 22. 1. 2010 Naslov: Re: Popravni kolokvij Postano: 12:13 pet, 22. 1. 2010 Naslov: Re: Popravni kolokvij |
    |
|
|
[quote="vuja"][quote="medonja"]http://web.math.hr/nastava/analiza/kol/ma1-0607-kp.pdf
dal netko moze rijesiti 3 zad iz ovog kolokvija...hvala..[/quote]
da bi dobio f(<0, ln5>) samo uvrstiš brojeve u funkciju. kad uvrstiš 0, dobiješ 1 - 8 + 12, što je jednako 5. kad uvrstiš ln5 dobiješ e^(2ln5) - 8e^(ln5) + 12. pošto ti je u eksponentu logaritam i baza logaritma jednaka bazi eksponencijalne fje, možeš spustiti eksponente i dobiješ 2ln5 - 8ln5 + 12 = 12 - 6 ln5 i to je cca 2.34, što je manje od 5. interval koji dobiješ je <12 - 6ln5, 5>. kad imaš prasliku na intervalu <-3, 0], znači da je f(x) iz tog intervala, odnosno da -3 < f(x) < 0. i rješavaš sustave dviju nejednadžbi, nađeš presjeke rješenja i to je konačno rješenje. ako ti je lakše, napraviš supstituciju e^x = t. nadam se da je ovo pomoglo :D[/quote]
mislim da bi to bilo predivno,kad bi bilo tako...a vuja,jel mi mozes onda rec koja bi bila slika f-je [latex] f(x) = x^2-3x+2[/latex] na intervalu [latex]<1,2>[/latex] ??
ugl. poanta,to mozes napravit u slucaju da je f-ja monotona na tom intervalu,ili u opcenitijem slucaju,ako je f-ja kompozicija dviju monotonih f-ja...pa imas ona pravila (rastuca i rastuca = rastuca, itd...),sto nije u ovom slucaju,ovde omas kopoziciju kvadratne i exponencijalne...sad nisan 100% siguran,al mislin da bi triba nac tjeme "parabole" (pod navodnike jer graf ovoga bas i nije parabola),odnosno x za koji ova f-ja postize svoj minimum...ako je ta tocka u zadanom intervalu, interval ce ti bit od f(min) do f(max) (max takoder iz intervala,prva ili zadnja tocka)...ukoliko min nije u intervalu,onda imas monotonost na tom intervalu i radis ono sta je kolega maloprije reka,samo ispravno...jer ovo "spustanje",nije opce tocno...prije nesto slicnije ovome [latex]f(ln5)=e^{2ln5}-8^{ln5}+12=5^2-8*5+12=-3[/latex],jer se ovaj [latex]e[/latex] i [latex]ln[/latex] "poniste" i "spusti" se petica...
nadan se da nisan zbunio
| vuja (napisa): | | medonja (napisa): | http://web.math.hr/nastava/analiza/kol/ma1-0607-kp.pdf
dal netko moze rijesiti 3 zad iz ovog kolokvija...hvala.. |
da bi dobio f(<0, ln5>) samo uvrstiš brojeve u funkciju. kad uvrstiš 0, dobiješ 1 - 8 + 12, što je jednako 5. kad uvrstiš ln5 dobiješ e^(2ln5) - 8e^(ln5) + 12. pošto ti je u eksponentu logaritam i baza logaritma jednaka bazi eksponencijalne fje, možeš spustiti eksponente i dobiješ 2ln5 - 8ln5 + 12 = 12 - 6 ln5 i to je cca 2.34, što je manje od 5. interval koji dobiješ je <12 - 6ln5, 5>. kad imaš prasliku na intervalu ←3, 0], znači da je f(x) iz tog intervala, odnosno da -3 < f(x) < 0. i rješavaš sustave dviju nejednadžbi, nađeš presjeke rješenja i to je konačno rješenje. ako ti je lakše, napraviš supstituciju e^x = t. nadam se da je ovo pomoglo  |
mislim da bi to bilo predivno,kad bi bilo tako...a vuja,jel mi mozes onda rec koja bi bila slika f-je 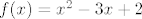 na intervalu na intervalu 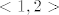 ?? ??
ugl. poanta,to mozes napravit u slucaju da je f-ja monotona na tom intervalu,ili u opcenitijem slucaju,ako je f-ja kompozicija dviju monotonih f-ja...pa imas ona pravila (rastuca i rastuca = rastuca, itd...),sto nije u ovom slucaju,ovde omas kopoziciju kvadratne i exponencijalne...sad nisan 100% siguran,al mislin da bi triba nac tjeme "parabole" (pod navodnike jer graf ovoga bas i nije parabola),odnosno x za koji ova f-ja postize svoj minimum...ako je ta tocka u zadanom intervalu, interval ce ti bit od f(min) do f(max) (max takoder iz intervala,prva ili zadnja tocka)...ukoliko min nije u intervalu,onda imas monotonost na tom intervalu i radis ono sta je kolega maloprije reka,samo ispravno...jer ovo "spustanje",nije opce tocno...prije nesto slicnije ovome 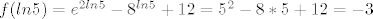 ,jer se ovaj ,jer se ovaj  i i 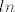 "poniste" i "spusti" se petica... "poniste" i "spusti" se petica...
nadan se da nisan zbunio
_________________
You'll take my life but I'll take yours too
You'll fire your musket but I'll run you through
So when you're waiting for the next attack
You'd better stand there's no turning back
|
|
| [Vrh] |
|
kaj
Forumaš(ica)

Pridružen/a: 15. 11. 2009. (21:02:20)
Postovi: (B8)16
|
|
| [Vrh] |
|
mornik
Forumaš(ica)

Pridružen/a: 26. 09. 2009. (06:25:44)
Postovi: (128)16
|
 Postano: 13:17 pet, 22. 1. 2010 Naslov: Re: Popravni kolokvij Postano: 13:17 pet, 22. 1. 2010 Naslov: Re: Popravni kolokvij |
    |
|
|
[quote="vuja"]da bi dobio f(<0, ln5>) samo uvrstiš brojeve u funkciju. kad uvrstiš 0, dobiješ 1 - 8 + 12, što je jednako 5. kad uvrstiš ln5 dobiješ e^(2ln5) - 8e^(ln5) + 12. pošto ti je u eksponentu logaritam i baza logaritma jednaka bazi eksponencijalne fje, možeš spustiti eksponente i dobiješ 2ln5 - 8ln5 + 12 = 12 - 6 ln5 i to je cca 2.34, što je manje od 5. interval koji dobiješ je <12 - 6ln5, 5>. kad imaš prasliku na intervalu <-3, 0], znači da je f(x) iz tog intervala, odnosno da -3 < f(x) < 0. i rješavaš sustave dviju nejednadžbi, nađeš presjeke rješenja i to je konačno rješenje. ako ti je lakše, napraviš supstituciju e^x = t. nadam se da je ovo pomoglo :D[/quote]
Ne baš :). Uz greške koje imaš u računu, postupak nije točan - to je relativno česta zamka u koju ljudi cijene upasti budući da je donekle prirodna, ali kao što je jkrstic objasnio, to možeš napraviti samo u nekim ekstremnim slučajevima, dok generalno to ne vrijedi :(.
Uglavnom, ovi su zadaci (ne ovi doslovno, ali takvi) riješeni već puno puta na forumu, tako da bi bilo korisno da pogledate malo ta rješenja, probate sami i onda kažete gdje ste zapeli.
Ovaj zadatak iz 2007. se rješava baš onako kao što ste radili milijun puta na vježbama i još smo milijun puta na forumu to komentirali - upotrebom kompozicija. Zapravo, to je dosta prirodan način - vidimo da nam je ova funkcija preteška da joj možemo nacrtati graf ili tako nešto, pa ju pokušavamo "podijeliti" na jednostavnije funkcije. Ukratko, uzmimo funkcije [latex]f_1(x)=x^2-8x+12[/latex] i [latex]f_2(x)=e^x[/latex] - u tom slučaju znamo da je [latex]f(x)=(f_1\circ f_2)(x)[/latex]. Sad imamo dvije tvrdnje koje su spomenute/dokazane na predavanjima/vježbama: [latex]f(A)=f_1(f_2(A))[/latex] i [latex]f^{-1}(B)=f_2^{-1}(f_1^{-1}(B))[/latex].
U a) dijelu zadatka uzmimo [latex]B=\langle -3,0\][/latex]. Prvo nas zanima [latex]f_1^{-1}(\langle -3,0\])[/latex], tj. kada je [latex]-3<f_1(x)=x^2-8x+12\leq 0[/latex]. To nije problem izračunati, naprosto riješimo dvije kvadratne jednadžbe. Ja ću sad to preskočiti budući da je dosta očito što bi trebalo činiti, a ti javi ako trebaš pomoć - uglavnom, dobivamo da je [latex]f_1^{-1}(\langle -3,0\])=\[2,3\rangle\cup\langle 5,6\][/latex]. Naposlijetku, zanima nas [latex]f_2^{-2}(\[2,3\rangle\cup\langle 5,6\])=f_2^{-2}(\[2,3\rangle)\cup f_2^{-2}(\langle 5,6\])[/latex]. No, to je lagano: nas, dakle, zanimaju sva rješenja od [latex]2\leq e^x<3[/latex] i [latex]5<e^x\leq 6[/latex] (naše rješenje je unija tih rješenja). Iz toga očito vidimo da je traženo rješenje [latex]\[\ln 2, \ln 3\rangle\cup\langle \ln 5,\ln 6\][/latex].
b) dio je lakši :). Uzimamo [latex]A=\[0,\ln 5\rangle[/latex]. Onda nas zanima [latex]f(A)=f_1(f_2(A))[/latex]. Riješimo prvo [latex]f_2(\[0,\ln 5\rangle)[/latex] - to je lagano i možemo "pročitati" rješenje s grafa ili (kao što je radio vuja tamo gdje nije smio :P), iskoristivši da je funkcija [latex]f_2(x)=e^x[/latex] rastuća i neprekidna, dobiti da je rješenje [latex]\[e^0,e^{\ln 5}\rangle=\[1,5\rangle[/latex]. Sad nas još zanima [latex]f_1(\[1,5\rangle)[/latex]. U svakom slučaju, s grafa ili računski ili na koji već način, možemo vidjeti da je rješenje [latex]\[-4,5\][/latex] - to je skup koji smo tražili.
U vezi 2. zadatka iz 2009., u a) dijelu ćemo lako pokazati indukcijom da je [latex]a_n\geq n[/latex] za sve [latex]n\in\mathbb{N}[/latex]. Kao rezultat, niz očito nije konvergentan (tj. divergira u [latex]+\infty[/latex]). Dakle, baza vrijedi. Neka je sad [latex]a_n\geq n[/latex] za neki [latex]n\in\mathbb{N}[/latex]. Pogledajmo [latex]a_{n+1}=2^{a_n}\geq 2^n[/latex] ([latex]2^x[/latex] je rastuća funkcija). Sad smo manje-više gotovi zato što znamo da za sve [latex]n\in\mathbb{N}[/latex] vrijedi [latex]2^n\geq n+1[/latex] - ako treba, to ponovno možemo dokazati indukcijom (u tom slučaju je baza opet trivijalna, a korak indukcije je [latex]2^{n+1}=2\cdot 2^n\geq 2n+2\geq n+2[/latex]). Dakle, pokazali smo da je [latex]a_{n+1}\geq n+1[/latex], pa smo gotovi sa indukcijom i sa zadatkom.
b) dio zadatka je puno tipičniji i isto se puno puta rješavao na svim mogućim formama nastave - niz je konvergentan i to ćemo pokazati tako da pokažemo da je monoton i ograničen (onda je, po poznatom teoremu, i konvergentan). Dobro, prvo pronađimo koji je limes ako postoji (dakle, mi u ovom trenutku ne znamo postoji li taj limes, ali ako postoji, znamo ga već i sada odrediti): vrijedi [latex]\displaystyle L=\lim_{n\to \infty} a_n=\lim_{n\to \infty} \frac{1}{3}a_{n-1}+2=\lim_{n\to \infty}\frac{1}{3}a_{n-1}+\lim_{n\to \infty}2=\frac{L}{3}+2[/latex]. Iz toga proizlazi da, ako postoji, limes je [latex]3[/latex].
Pokažimo da je sada niz ograničen. Budući da se očito radi o zbrajanju pozitivnih brojeva, niz je sigurno odozdo ograničen (ako treba, formalno možemo ići indukcijom i iskoristiti da iz [latex]a_{n-1}>0[/latex] lako slijedi, po definicionoj relaciji, da je [latex]a_n>0[/latex]). Preostaje ograničenost odozgo: dokazat ćemo da je [latex]a_n<3[/latex] za svaki [latex]L[/latex]. Ponovno idemo indukcijom - baza očito vrijedi, a ako je [latex]a_n<3[/latex], onda je [latex]\displaystyle a_{n+1}=\frac{a_n}{3}+2<\frac{3}{3}+2=3[/latex]. Stoga smo s tim dijelom gotovi.
Treba još pokazati da je niz monoton - i to je lagano. Vidimo da je [latex]a_{n+1}>a_n[/latex] ekvivalentno s [latex]\displaystyle \frac{a_n}{3}+2>a_n[/latex], a to je opet ekvivalentno s [latex]a_n<3[/latex], što smo upravo dokazali. Dakle, niz je monoton (i to strogo rastuć) i ograničen, pa je i konvergentan. Dakle, ima limes, a već smo prije pokazali da je taj limes onda nužno jednak [latex]3[/latex].
Evo, nadam se da sam pomogao, a, kažem, ovakvih zadataka ima na forumu "na bacanje", tako da pogledajte malo i pitajte ako ste zapeli negdje, to ispada dosta smislenije od toga da treba riješiti cijeli zadatak :lol:.
EDIT: Sorry, kaj, nisam vidio tvoje rješenje :).
| vuja (napisa): | da bi dobio f(<0, ln5>) samo uvrstiš brojeve u funkciju. kad uvrstiš 0, dobiješ 1 - 8 + 12, što je jednako 5. kad uvrstiš ln5 dobiješ e^(2ln5) - 8e^(ln5) + 12. pošto ti je u eksponentu logaritam i baza logaritma jednaka bazi eksponencijalne fje, možeš spustiti eksponente i dobiješ 2ln5 - 8ln5 + 12 = 12 - 6 ln5 i to je cca 2.34, što je manje od 5. interval koji dobiješ je <12 - 6ln5, 5>. kad imaš prasliku na intervalu ←3, 0], znači da je f(x) iz tog intervala, odnosno da -3 < f(x) < 0. i rješavaš sustave dviju nejednadžbi, nađeš presjeke rješenja i to je konačno rješenje. ako ti je lakše, napraviš supstituciju e^x = t. nadam se da je ovo pomoglo  |
Ne baš  . Uz greške koje imaš u računu, postupak nije točan - to je relativno česta zamka u koju ljudi cijene upasti budući da je donekle prirodna, ali kao što je jkrstic objasnio, to možeš napraviti samo u nekim ekstremnim slučajevima, dok generalno to ne vrijedi . Uz greške koje imaš u računu, postupak nije točan - to je relativno česta zamka u koju ljudi cijene upasti budući da je donekle prirodna, ali kao što je jkrstic objasnio, to možeš napraviti samo u nekim ekstremnim slučajevima, dok generalno to ne vrijedi  . .
Uglavnom, ovi su zadaci (ne ovi doslovno, ali takvi) riješeni već puno puta na forumu, tako da bi bilo korisno da pogledate malo ta rješenja, probate sami i onda kažete gdje ste zapeli.
Ovaj zadatak iz 2007. se rješava baš onako kao što ste radili milijun puta na vježbama i još smo milijun puta na forumu to komentirali - upotrebom kompozicija. Zapravo, to je dosta prirodan način - vidimo da nam je ova funkcija preteška da joj možemo nacrtati graf ili tako nešto, pa ju pokušavamo "podijeliti" na jednostavnije funkcije. Ukratko, uzmimo funkcije 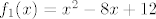 i i 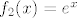 - u tom slučaju znamo da je - u tom slučaju znamo da je 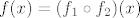 . Sad imamo dvije tvrdnje koje su spomenute/dokazane na predavanjima/vježbama: . Sad imamo dvije tvrdnje koje su spomenute/dokazane na predavanjima/vježbama: 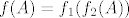 i i 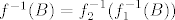 . .
U a) dijelu zadatka uzmimo 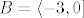 . Prvo nas zanima . Prvo nas zanima 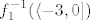 , tj. kada je , tj. kada je 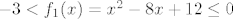 . To nije problem izračunati, naprosto riješimo dvije kvadratne jednadžbe. Ja ću sad to preskočiti budući da je dosta očito što bi trebalo činiti, a ti javi ako trebaš pomoć - uglavnom, dobivamo da je . To nije problem izračunati, naprosto riješimo dvije kvadratne jednadžbe. Ja ću sad to preskočiti budući da je dosta očito što bi trebalo činiti, a ti javi ako trebaš pomoć - uglavnom, dobivamo da je 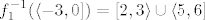 . Naposlijetku, zanima nas . Naposlijetku, zanima nas 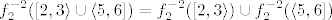 . No, to je lagano: nas, dakle, zanimaju sva rješenja od . No, to je lagano: nas, dakle, zanimaju sva rješenja od 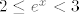 i i 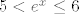 (naše rješenje je unija tih rješenja). Iz toga očito vidimo da je traženo rješenje (naše rješenje je unija tih rješenja). Iz toga očito vidimo da je traženo rješenje 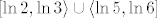 . .
b) dio je lakši  . Uzimamo . Uzimamo 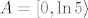 . Onda nas zanima . Onda nas zanima 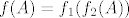 . Riješimo prvo . Riješimo prvo 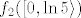 - to je lagano i možemo "pročitati" rješenje s grafa ili (kao što je radio vuja tamo gdje nije smio - to je lagano i možemo "pročitati" rješenje s grafa ili (kao što je radio vuja tamo gdje nije smio  ), iskoristivši da je funkcija ), iskoristivši da je funkcija 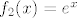 rastuća i neprekidna, dobiti da je rješenje rastuća i neprekidna, dobiti da je rješenje 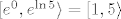 . Sad nas još zanima . Sad nas još zanima 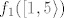 . U svakom slučaju, s grafa ili računski ili na koji već način, možemo vidjeti da je rješenje . U svakom slučaju, s grafa ili računski ili na koji već način, možemo vidjeti da je rješenje 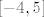 - to je skup koji smo tražili. - to je skup koji smo tražili.
U vezi 2. zadatka iz 2009., u a) dijelu ćemo lako pokazati indukcijom da je  za sve za sve 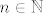 . Kao rezultat, niz očito nije konvergentan (tj. divergira u . Kao rezultat, niz očito nije konvergentan (tj. divergira u  ). Dakle, baza vrijedi. Neka je sad ). Dakle, baza vrijedi. Neka je sad  za neki za neki 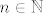 . Pogledajmo . Pogledajmo 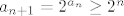 ( (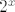 je rastuća funkcija). Sad smo manje-više gotovi zato što znamo da za sve je rastuća funkcija). Sad smo manje-više gotovi zato što znamo da za sve 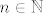 vrijedi vrijedi 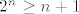 - ako treba, to ponovno možemo dokazati indukcijom (u tom slučaju je baza opet trivijalna, a korak indukcije je - ako treba, to ponovno možemo dokazati indukcijom (u tom slučaju je baza opet trivijalna, a korak indukcije je 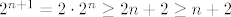 ). Dakle, pokazali smo da je ). Dakle, pokazali smo da je 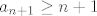 , pa smo gotovi sa indukcijom i sa zadatkom. , pa smo gotovi sa indukcijom i sa zadatkom.
b) dio zadatka je puno tipičniji i isto se puno puta rješavao na svim mogućim formama nastave - niz je konvergentan i to ćemo pokazati tako da pokažemo da je monoton i ograničen (onda je, po poznatom teoremu, i konvergentan). Dobro, prvo pronađimo koji je limes ako postoji (dakle, mi u ovom trenutku ne znamo postoji li taj limes, ali ako postoji, znamo ga već i sada odrediti): vrijedi 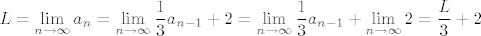 . Iz toga proizlazi da, ako postoji, limes je . Iz toga proizlazi da, ako postoji, limes je 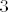 . .
Pokažimo da je sada niz ograničen. Budući da se očito radi o zbrajanju pozitivnih brojeva, niz je sigurno odozdo ograničen (ako treba, formalno možemo ići indukcijom i iskoristiti da iz 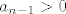 lako slijedi, po definicionoj relaciji, da je lako slijedi, po definicionoj relaciji, da je 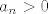 ). Preostaje ograničenost odozgo: dokazat ćemo da je ). Preostaje ograničenost odozgo: dokazat ćemo da je 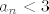 za svaki za svaki  . Ponovno idemo indukcijom - baza očito vrijedi, a ako je . Ponovno idemo indukcijom - baza očito vrijedi, a ako je 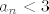 , onda je , onda je 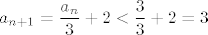 . Stoga smo s tim dijelom gotovi. . Stoga smo s tim dijelom gotovi.
Treba još pokazati da je niz monoton - i to je lagano. Vidimo da je 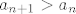 ekvivalentno s ekvivalentno s 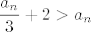 , a to je opet ekvivalentno s , a to je opet ekvivalentno s 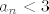 , što smo upravo dokazali. Dakle, niz je monoton (i to strogo rastuć) i ograničen, pa je i konvergentan. Dakle, ima limes, a već smo prije pokazali da je taj limes onda nužno jednak , što smo upravo dokazali. Dakle, niz je monoton (i to strogo rastuć) i ograničen, pa je i konvergentan. Dakle, ima limes, a već smo prije pokazali da je taj limes onda nužno jednak 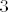 . .
Evo, nadam se da sam pomogao, a, kažem, ovakvih zadataka ima na forumu "na bacanje", tako da pogledajte malo i pitajte ako ste zapeli negdje, to ispada dosta smislenije od toga da treba riješiti cijeli zadatak  . .
EDIT: Sorry, kaj, nisam vidio tvoje rješenje  . .
|
|
| [Vrh] |
|
vuja
Forumaš(ica)


Pridružen/a: 26. 09. 2009. (12:57:07)
Postovi: (2C)16
Spol: 
|
|
| [Vrh] |
|
c4rimson
Forumaš(ica)

Pridružen/a: 11. 01. 2010. (18:57:26)
Postovi: (3B)16
|
|
| [Vrh] |
|
kaj
Forumaš(ica)

Pridružen/a: 15. 11. 2009. (21:02:20)
Postovi: (B8)16
|
 Postano: 20:32 pet, 22. 1. 2010 Naslov: Postano: 20:32 pet, 22. 1. 2010 Naslov: |
    |
|
|
[quote="c4rimson"]http://web.math.hr/nastava/analiza/kol/ma1-0708-kp.pdf
Trebam pomoc kod 5. zadatka pod a.
Znam da ide supstitucija t=1-x i da je x=1-t i da t->0, al kad to uvrstim, nikako mi ne ispada.[/quote]
pretpostavljam da misliš B grupa jer tamo x ide u 1
ovdje supstitucija neće raditi kako si se vjerojatno već i sam uvjerio
primijeti da u brojniku imaš razliku kvadrata, i da se općenito sin(x) može napisati kao sin(pi-x) , sad sve pomnoži sa pi/pi i upari (pi-pi*x) iz brojnika i sin(pi-pi*x) iz nazivnika (pošto x ide u jedan, (pi-pi*x) ide u nulu) pa (pi-pi*x/sin(pi-pi*x)) ide u 1 i ono što ti ostaje to je definirano , nadam se da je jasno :D
| c4rimson (napisa): | http://web.math.hr/nastava/analiza/kol/ma1-0708-kp.pdf
Trebam pomoc kod 5. zadatka pod a.
Znam da ide supstitucija t=1-x i da je x=1-t i da t→0, al kad to uvrstim, nikako mi ne ispada. |
pretpostavljam da misliš B grupa jer tamo x ide u 1
ovdje supstitucija neće raditi kako si se vjerojatno već i sam uvjerio
primijeti da u brojniku imaš razliku kvadrata, i da se općenito sin(x) može napisati kao sin(pi-x) , sad sve pomnoži sa pi/pi i upari (pi-pi*x) iz brojnika i sin(pi-pi*x) iz nazivnika (pošto x ide u jedan, (pi-pi*x) ide u nulu) pa (pi-pi*x/sin(pi-pi*x)) ide u 1 i ono što ti ostaje to je definirano , nadam se da je jasno 
|
|
| [Vrh] |
|
Darija.x
Forumaš(ica)
Pridružen/a: 10. 07. 2008. (18:31:47)
Postovi: (34)16
Lokacija: Velika Gorica
|
|
| [Vrh] |
|
kaj
Forumaš(ica)

Pridružen/a: 15. 11. 2009. (21:02:20)
Postovi: (B8)16
|
 Postano: 21:04 pet, 22. 1. 2010 Naslov: Postano: 21:04 pet, 22. 1. 2010 Naslov: |
    |
|
|
[quote="Darija.x"]može mala pomoć oko ovog zadatka?
http://web.math.hr/nastava/analiza/kol/ma1-0809-popr.pdf
riješila sam ga na jedan način - za koji mi je rečeno da nije sasvim točan :/
- znam da ga rastavljamo na dva skupa - za paran i neparan n, znači za n=2k i n=2k-1
-nakon što to uvrstimo umjesto n (naravno u svaki skup posebno) - kod prvog skupa uvrštavam prvo k=1, dobijem niz- pa taj niz provjeravam da li je rastuć ili padajuć? Te da li onda uvrštavam m=1 da dobijem neku među, a onda od istog tog niza tražim limes? (i naravno - onda repeat za drugi skup)
- nadam se da će sve biti shvaćeno što sam i kako mislila :/[/quote]
Nakon što uvrstiš n=2k dobiješ niz. Primijeti da je tada onaj izraz u najmanjem cijelom konstanta (koja?) za sve prirodne brojeve k. Nakon toga moraš odrediti da li je niz sa varijablom m rastući ili padajući, ako je rastući limes mu je supremum, a prvi član infimum, ujedno i minimum. Ako je niz padajući limes mu je infimum ,a prvi član supremum (i maksimum).Može se dogoditi i da niz nije monoton (da nije niti rastući niti padajući).
Za n=2k-1 ide analogno. Kad to sve napraviš ukupni supremum je maksimum od ova dva supremuma, a konačni infimum je minimum ta dva infimuma. :D
| Darija.x (napisa): | može mala pomoć oko ovog zadatka?
http://web.math.hr/nastava/analiza/kol/ma1-0809-popr.pdf
riješila sam ga na jedan način - za koji mi je rečeno da nije sasvim točan 
- znam da ga rastavljamo na dva skupa - za paran i neparan n, znači za n=2k i n=2k-1
-nakon što to uvrstimo umjesto n (naravno u svaki skup posebno) - kod prvog skupa uvrštavam prvo k=1, dobijem niz- pa taj niz provjeravam da li je rastuć ili padajuć? Te da li onda uvrštavam m=1 da dobijem neku među, a onda od istog tog niza tražim limes? (i naravno - onda repeat za drugi skup)
- nadam se da će sve biti shvaćeno što sam i kako mislila  |
Nakon što uvrstiš n=2k dobiješ niz. Primijeti da je tada onaj izraz u najmanjem cijelom konstanta (koja?) za sve prirodne brojeve k. Nakon toga moraš odrediti da li je niz sa varijablom m rastući ili padajući, ako je rastući limes mu je supremum, a prvi član infimum, ujedno i minimum. Ako je niz padajući limes mu je infimum ,a prvi član supremum (i maksimum).Može se dogoditi i da niz nije monoton (da nije niti rastući niti padajući).
Za n=2k-1 ide analogno. Kad to sve napraviš ukupni supremum je maksimum od ova dva supremuma, a konačni infimum je minimum ta dva infimuma. 
|
|
| [Vrh] |
|
mornik
Forumaš(ica)

Pridružen/a: 26. 09. 2009. (06:25:44)
Postovi: (128)16
|
 Postano: 21:11 pet, 22. 1. 2010 Naslov: Postano: 21:11 pet, 22. 1. 2010 Naslov: |
    |
|
|
Hm, nisam baš siguran da sam dobro shvatio što si htjela reći :), pa ću probati objasniti svojim riječima što bi trebalo, a ti onda reci je li to isto onome što si ti zamislila :).
Dakle, ideja dijeljenja za na parne i neparne [latex]n[/latex] je u redu, ali idemo prije toga razriješiti samo jednu laganu stvar: za sve prirodne [latex]n[/latex] vrijedi [latex]\displaystyle 0\leq\frac{2n-1}{n^2+1}<1[/latex], to se trivijalno provjeri. Stoga je [latex]\displaystyle\lfloor\frac{2n-1}{n^2+1}\rfloor=0[/latex], pa nam to olakšava stvar. Inače, ideja za ovo je relativno jasna - znamo da je (za dovoljno velike [latex]n[/latex]) [latex]2n-1[/latex] "puno manje" od [latex]n^2+1[/latex], pa idemo naći neko ograničenje, tako da se idealno riješimo ovog najvećeg cijelog jer taj izraz nije baš lijep :). Ispada da je to ograničenje baš idealno :).
No, dakle, nas zanima [latex]\displaystyle\frac{(-1)^nm}{2m-1}[/latex]. Sad "rastavimo" [latex]n[/latex] na parne i neparne i primijetimo da nam zapravo parnost od [latex]n[/latex] jedino igra ulogu (tj. ne igra nam ulogu koliki je [latex]n[/latex], nego samo je li paran ili ne).
Ako je [latex]n[/latex] paran, imamo skup/niz [latex]\displaystyle\frac{m}{2m-1}[/latex], a ako je neparan, imamo skup/niz [latex]\displaystyle\frac{-m}{2m-1}[/latex]. Pronađemo supremume i infimume tih skupova (jedno će biti limes, a drugo vrijednost za [latex]m=1[/latex], budući da su ti nizovi monotoni, što si i ti spomenula, a budući da su ti nizovi zapravo isti do na predznak, znamo da je supremum jednog infimum drugog i obrnuto) i lako dobivamo završno rješenje: supremum je onaj veći od dva supremuma koji si dobila, mislim da bi trebao biti [latex]1[/latex], a infimum manji od dva infimuma koje dobivamo i mislim da bi trebao biti [latex]-1[/latex].
I opet me kaj pretekao :), ali nije mi se dalo sad brisati cijeli ovaj post kad sam ga napisao :|.
Hm, nisam baš siguran da sam dobro shvatio što si htjela reći  , pa ću probati objasniti svojim riječima što bi trebalo, a ti onda reci je li to isto onome što si ti zamislila , pa ću probati objasniti svojim riječima što bi trebalo, a ti onda reci je li to isto onome što si ti zamislila  . .
Dakle, ideja dijeljenja za na parne i neparne  je u redu, ali idemo prije toga razriješiti samo jednu laganu stvar: za sve prirodne je u redu, ali idemo prije toga razriješiti samo jednu laganu stvar: za sve prirodne  vrijedi vrijedi 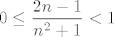 , to se trivijalno provjeri. Stoga je , to se trivijalno provjeri. Stoga je 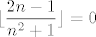 , pa nam to olakšava stvar. Inače, ideja za ovo je relativno jasna - znamo da je (za dovoljno velike , pa nam to olakšava stvar. Inače, ideja za ovo je relativno jasna - znamo da je (za dovoljno velike  ) ) 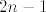 "puno manje" od "puno manje" od 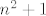 , pa idemo naći neko ograničenje, tako da se idealno riješimo ovog najvećeg cijelog jer taj izraz nije baš lijep , pa idemo naći neko ograničenje, tako da se idealno riješimo ovog najvećeg cijelog jer taj izraz nije baš lijep  . Ispada da je to ograničenje baš idealno . Ispada da je to ograničenje baš idealno  . .
No, dakle, nas zanima 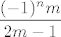 . Sad "rastavimo" . Sad "rastavimo"  na parne i neparne i primijetimo da nam zapravo parnost od na parne i neparne i primijetimo da nam zapravo parnost od  jedino igra ulogu (tj. ne igra nam ulogu koliki je jedino igra ulogu (tj. ne igra nam ulogu koliki je  , nego samo je li paran ili ne). , nego samo je li paran ili ne).
Ako je  paran, imamo skup/niz paran, imamo skup/niz 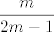 , a ako je neparan, imamo skup/niz , a ako je neparan, imamo skup/niz 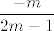 . Pronađemo supremume i infimume tih skupova (jedno će biti limes, a drugo vrijednost za . Pronađemo supremume i infimume tih skupova (jedno će biti limes, a drugo vrijednost za 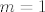 , budući da su ti nizovi monotoni, što si i ti spomenula, a budući da su ti nizovi zapravo isti do na predznak, znamo da je supremum jednog infimum drugog i obrnuto) i lako dobivamo završno rješenje: supremum je onaj veći od dva supremuma koji si dobila, mislim da bi trebao biti , budući da su ti nizovi monotoni, što si i ti spomenula, a budući da su ti nizovi zapravo isti do na predznak, znamo da je supremum jednog infimum drugog i obrnuto) i lako dobivamo završno rješenje: supremum je onaj veći od dva supremuma koji si dobila, mislim da bi trebao biti  , a infimum manji od dva infimuma koje dobivamo i mislim da bi trebao biti , a infimum manji od dva infimuma koje dobivamo i mislim da bi trebao biti  . .
I opet me kaj pretekao  , ali nije mi se dalo sad brisati cijeli ovaj post kad sam ga napisao , ali nije mi se dalo sad brisati cijeli ovaj post kad sam ga napisao  . .
|
|
| [Vrh] |
|
Darija.x
Forumaš(ica)
Pridružen/a: 10. 07. 2008. (18:31:47)
Postovi: (34)16
Lokacija: Velika Gorica
|
|
| [Vrh] |
|
kre5o
Forumaš(ica)
Pridružen/a: 14. 09. 2009. (22:20:52)
Postovi: (32)16
|
|
| [Vrh] |
|
kaj
Forumaš(ica)

Pridružen/a: 15. 11. 2009. (21:02:20)
Postovi: (B8)16
|
|
| [Vrh] |
|
Darija.x
Forumaš(ica)
Pridružen/a: 10. 07. 2008. (18:31:47)
Postovi: (34)16
Lokacija: Velika Gorica
|
 Postano: 15:22 sub, 23. 1. 2010 Naslov: Postano: 15:22 sub, 23. 1. 2010 Naslov: |
    |
|
|
kre5o:
1. zadatak
raspiši funkciju na kompozicije
f1(x) = cosx
f2(x) = arcsinx
i nađi sliku od intervala [pi,2pi]
slika koji bi trebao dobiti ti je -> [-(pi/2), (pi/2)]
znači, imaš da ti je f(pi) = -(pi/2), te f(2pi)= pi/2
ti trebaš naći a i b, tako da ih samo uvrstiš u f(x)=ax + b za prvi slučaj da ti je x=pi, a drugi slučaj da ti je x=2pi
sustav ti ispadne a*pi + b = -(pi/2)
a*2pi + b = pi/2
..dalje znaš :)
kre5o:
1. zadatak
raspiši funkciju na kompozicije
f1(x) = cosx
f2(x) = arcsinx
i nađi sliku od intervala [pi,2pi]
slika koji bi trebao dobiti ti je → [-(pi/2), (pi/2)]
znači, imaš da ti je f(pi) = -(pi/2), te f(2pi)= pi/2
ti trebaš naći a i b, tako da ih samo uvrstiš u f(x)=ax + b za prvi slučaj da ti je x=pi, a drugi slučaj da ti je x=2pi
sustav ti ispadne a*pi + b = -(pi/2)
a*2pi + b = pi/2
..dalje znaš 
|
|
| [Vrh] |
|
kre5o
Forumaš(ica)
Pridružen/a: 14. 09. 2009. (22:20:52)
Postovi: (32)16
|
|
| [Vrh] |
|
Darija.x
Forumaš(ica)
Pridružen/a: 10. 07. 2008. (18:31:47)
Postovi: (34)16
Lokacija: Velika Gorica
|
|
| [Vrh] |
|
kaj
Forumaš(ica)

Pridružen/a: 15. 11. 2009. (21:02:20)
Postovi: (B8)16
|
 Postano: 17:52 sub, 23. 1. 2010 Naslov: Postano: 17:52 sub, 23. 1. 2010 Naslov: |
    |
|
|
[quote="Darija.x"]Kako bi bilo najtočnije zapisati rješenje tipa kada tražimo prasliku sin-a na intervalu od [0,1] - ono obuhvaća sve intervale (..[-2pi,-pi]U[0,pi]U[2pi,3pi]U...) - na prvom kolokviju je bila masa grešaka oko točnog formuliranja zapisa tog intervala :/[/quote]
U (ispod toga malim slovima "k element Z") [2kpi,(2k-1)pi] :)
(sori šta neznam pisat u Latexu)
| Darija.x (napisa): | Kako bi bilo najtočnije zapisati rješenje tipa kada tražimo prasliku sin-a na intervalu od [0,1] - ono obuhvaća sve intervale (..[-2pi,-pi]U[0,pi]U[2pi,3pi]U...) - na prvom kolokviju je bila masa grešaka oko točnog formuliranja zapisa tog intervala  |
U (ispod toga malim slovima "k element Z") [2kpi,(2k-1)pi] 
(sori šta neznam pisat u Latexu)
|
|
| [Vrh] |
|
Darija.x
Forumaš(ica)
Pridružen/a: 10. 07. 2008. (18:31:47)
Postovi: (34)16
Lokacija: Velika Gorica
|
 Postano: 18:16 sub, 23. 1. 2010 Naslov: Postano: 18:16 sub, 23. 1. 2010 Naslov: |
    |
|
|
[quote="kaj"][quote="Darija.x"]Kako bi bilo najtočnije zapisati rješenje tipa kada tražimo prasliku sin-a na intervalu od [0,1] - ono obuhvaća sve intervale (..[-2pi,-pi]U[0,pi]U[2pi,3pi]U...) - na prvom kolokviju je bila masa grešaka oko točnog formuliranja zapisa tog intervala :/[/quote]
U (ispod toga malim slovima "k element Z") [2kpi,(2k-1)pi] :)
(sori šta neznam pisat u Latexu)[/quote]
ma jooj ;) sve je usvojeno ;)
hvala ti :)
| kaj (napisa): | | Darija.x (napisa): | Kako bi bilo najtočnije zapisati rješenje tipa kada tražimo prasliku sin-a na intervalu od [0,1] - ono obuhvaća sve intervale (..[-2pi,-pi]U[0,pi]U[2pi,3pi]U...) - na prvom kolokviju je bila masa grešaka oko točnog formuliranja zapisa tog intervala  |
U (ispod toga malim slovima "k element Z") [2kpi,(2k-1)pi] 
(sori šta neznam pisat u Latexu) |
ma jooj  sve je usvojeno sve je usvojeno 
hvala ti 
|
|
| [Vrh] |
|
|







